时序预测 | MATLAB实现EEMD-GRU、GRU集合经验模态分解结合门控循环单元时间序列预测对比

时序预测 | MATLAB实现EEMD-GRU、GRU集合经验模态分解结合门控循环单元时间序列预测对比

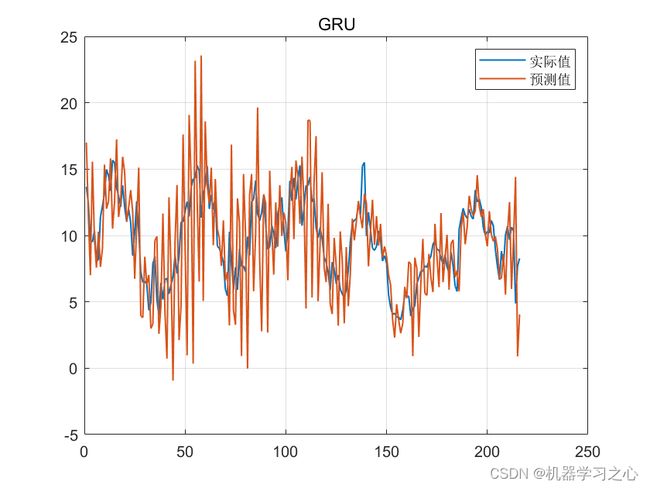
效果一览

基本介绍

1.MATLAB实现EEMD-GRU、GRU时间序列预测对比;
2.时间序列预测 就是先eemd把原输入全分解变成很多维作为输入 ， 再输入GRU预测 ;
3.运行环境Matlab2020b及以上，输出RMSE、MAPE、MAE等多指标对比，
先运行main1_eemd_test，进行eemd分解；再运行main2_gru、main3_eemd_gru；再运行main4_compare，两个模型对比。
程序乱码是由于Matlab版本不一致造成的，处理方式如下：先重新下载程序，如XXX.m程序出现乱码，则在文件夹中找到XXX.m，右击选择打开方式为记事本文本文档（txt），查看文档是否乱码，通常不乱码，则删除Matlab中的XXX.m的全部代码，将文本文档中不乱码的代码复制到Matlab中的XXX.m中。

模型搭建

EEMD-GRU (Ensemble Empirical Mode Decomposition - Gated Recurrent Unit) 是一种将 EEMD 和 GRU 结合起来进行时间序列预测的方法。EEMD 用于将原始时间序列分解成多个固有模态函数 (Intrinsic Mode Functions, IMFs)，然后 GRU 用于对这些 IMFs 进行建模和预测。
EEMD 是一种数据分解方法，将时间序列分解成多个 IMFs 和一个残差项。IMFs 是具有不同频率和振幅特征的函数，可以表示原始时间序列的不同成分。GRU (Gated Recurrent Unit):GRU 是一种循环神经网络 (Recurrent Neural Network, RNN) 的变体，具有门控机制，可以捕捉时间序列中的长期依赖关系。GRU 通过门控单元来控制信息的流动和记忆的更新。
EEMD-GRU 时间序列预测过程:
a. 将原始时间序列进行 EEMD 分解，得到多个 IMFs 和一个残差项。
b. 将每个 IMF 作为 GRU 的输入序列，训练多个 GRU 模型，每个模型对应一个 IMF。
c. 对于每个 GRU 模型，使用历史时刻的输入序列预测下一个时刻的值。
d. 将每个 GRU 模型的预测结果加权求和，得到最终的时间序列预测结果。
EEMD-GRU 时间序列预测公式:
假设有 N 个 IMFs，第 i 个 IMF 的 GRU 模型表示为 GRU_i。
对于第 i 个 GRU 模型，其输入序列为 X_i = [x_i1, x_i2, …, x_iT]，其中 x_ij 表示第 i 个 IMF 在时间 j 的值。
模型 GRU_i 的预测结果为 y_i = [y_i1, y_i2, …, y_iT]，其中 y_ij 表示模型 GRU_i 在时间 j 的预测值。
最终的时间序列预测结果为 y = w_1 * y_1 + w_2 * y_2 + … + w_N * y_N，其中 w_i 表示第 i 个 GRU 模型的权重。
以上是 EEMD-GRU 时间序列预测的基本原理和公式，通过将 EEMD 的分解结果与 GRU 的建模能力相结合，可以更好地捕捉时间序列的特征和趋势，提高预测的准确性。

程序设计

• 完整程序和数据获取方式1：私信博主回复MATLAB实现EEMD-GRU、GRU集合经验模态分解结合门控循环单元时间序列预测对比，同等价值程序兑换；
• 完整程序和数据下载方式2(资源处直接下载)：MATLAB实现EEMD-GRU、GRU集合经验模态分解结合门控循环单元时间序列预测对比；

%% 创建混合网络架构
% 输入特征维度
numFeatures  = f_;
% 输出特征维度
numResponses = 1;
FiltZise = 10;
%  
    layers = [...
        % 输入特征
        sequenceInputLayer([numFeatures 1 1],'Name','input')
        sequenceFoldingLayer('Name','fold')

        dropoutLayer(0.25,'Name','drop3')
        % 全连接层
        fullyConnectedLayer(numResponses,'Name','fc')
        regressionLayer('Name','output')    ];

    layers = layerGraph(layers);
    layers = connectLayers(layers,'fold/miniBatchSize','unfold/miniBatchSize');

%% 
% 批处理样本
MiniBatchSize =128;
% 最大迭代次数
MaxEpochs = 500;
    options = trainingOptions( 'adam', ...
        'MaxEpochs',500, ...
        'GradientThreshold',1, ...
        'InitialLearnRate',optVars.InitialLearnRate, ...
        'LearnRateSchedule','piecewise', ...
        'LearnRateDropPeriod',400, ...
        'LearnRateDropFactor',0.2, ...
        'L2Regularization',optVars.L2Regularization,...
        'Verbose',false, ...
        'Plots','none');

%% 训练混合网络
net = trainNetwork(XrTrain,YrTrain,layers,options);
desvio_estandar=std(x);
x=x/desvio_estandar;
xconruido=x+Nstd*randn(size(x));
[modos, o, it]=emd(xconruido,'MAXITERATIONS',MaxIter);
modos=modos/NR;
iter=it;
if NR>=2
    for i=2:NR
        xconruido=x+Nstd*randn(size(x));
        [temp, ort, it]=emd(xconruido,'MAXITERATIONS',MaxIter);
        temp=temp/NR;
        lit=length(it);
        [p liter]=size(iter);
        if lit<liter
            it=[it zeros(1,liter-lit)];
        end;
        if liter<lit
            iter=[iter zeros(p,lit-liter)];
        end;
        
        iter=[iter;it];
        
        [filas columnas]=size(temp);
        [alto ancho]=size(modos);
        diferencia=alto-filas;
        if filas>alto
            modos=[modos; zeros(abs(diferencia),ancho)];
        end;
        if alto>filas
            temp=[temp;zeros(abs(diferencia),ancho)];
        end;
        
        modos=modos+temp;
    end;
end;
its=iter;
modos=modos*desvio_estandar;

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/129036772?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128690229