选择排序详解

选择排序详解

​ 摘要：选择排序算法是一种比较容易理解的排序算法，记得我在第一次学习C语言的时候，老师让我们自己尝试写一个排序，我们很多人下意识写出来的就是一种具有选择排序思想的排序算法，只不过那种算法会花费一个额外的数组进行存储，在学习了选择排序算法之后，我知道了那个数组是没有必要声明的。

1.选择排序算法详解

1.药引子——我自己的排序方法

​ 选择排序是一种非常基础的排序算法，其排序关键在于：使用查找最大值/最小值的方法，查询出数组中的最大/最小值，然后将这个最大/最小值放到数组的最后/最前边，现在，我们用我刚学C语言时的那种选择手段进行理解：

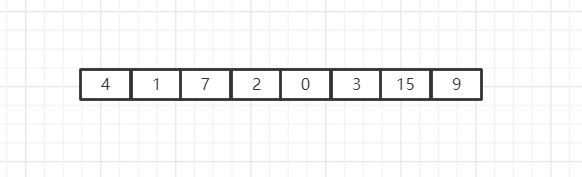
​ 首先我们得到一个数组之后：

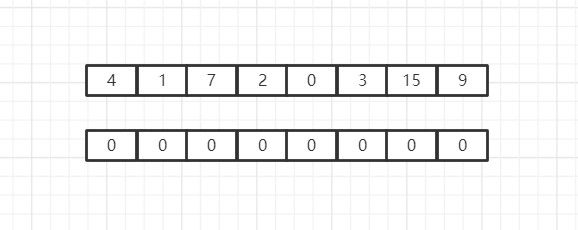
​ 我们要创建一片和这个数组一样大的数组区域，用于存储已经排好序的新数组：

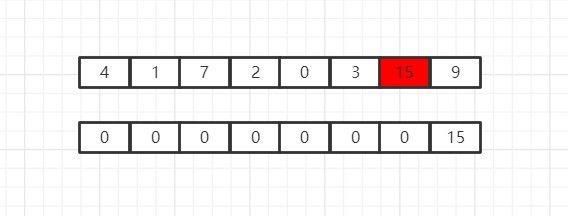
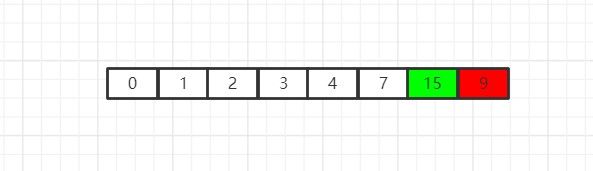
​ 现在，我们开始对数组进行最大值选取，数组中找最大值的方法想必大家都会，因此在这里不再赘述，总之我们在第一次会找到15，找到之后我们将15放在新数组的最后边：

​ 如上图所示，我们使用某种方式，反正就是在下次寻找最大值的时候，不再考虑15了，然后重复找最大值然后放在新数组中的这个过程，这样将整个数组都标记完之后，我们就能对这个数组排序。然而，这个方法效率太低了，首先就是标记这个事情，就很难办，当初我是使用了另外一个新数组来存储已经被当成过最大值的数，每次在遍历到一个原数组中的值后，都会现在这个标记数组中查一下，如果它不存在标记数组中，那么我再考虑它是否是最大值这件事，总之这种方法既浪费空间，又浪费时间，不知道人类早期有没有用过我这种方法，我想如果早期的程序员们如果都是精英的话，那肯定连想到都不会想到我这种双浪费的方法。然而我的这个基础方法虽然简单，但是已经体现出了选择排序的思想了，那就是找最大/最小值，然后将它们放在属于自己的合适位置。

2.命根子——选择排序的精髓

​ 现在我们来正式开始讲解选择排序，选择排序是一种简单基础好理解的排序方法，但我仍然要记录一下。首先我们在上文中已经透露了选择排序的思想，那么选择排序是如何高效的完成这个排序行为的呢？首先我们需要理解的是：排序行为，本身可以理解为让数字们移动到各自合适的位置的过程。这个思想将在归并排序中有更加明显的体现，既然排序行为是让数字们各归其位的过程，那我们如何知道哪个数字应该去哪个位置呢？也许人类能一眼看出，但是计算机却没有人类那么聪明，因此我们不得不使用更简单的方式告诉计算机：一个数组中的数字，最大的一定在最后边，最小的一定在最前边，计算机秉持着这个指令，就可以在找到最大的数字之后将其放到最后边或者将最小的数字放到最前边，然后…然后呢？计算机可以找到一个数组中最大的或者最小的数字，但是它能找到次大或者次小的吗？答案仍然是不可以，计算机没有这么智能，因此我们还要告诉计算机一个指令，那就是在将当前数组的最大值放到最后边或者将数组的最小值放到最前边之后，你要缩小这个数组的规模，不再考虑最后一位或者最前一位，你要在这个缩小规模的新数组中重新重复刚才的行为。好了，这就是选择排序。

3.选择排序图解

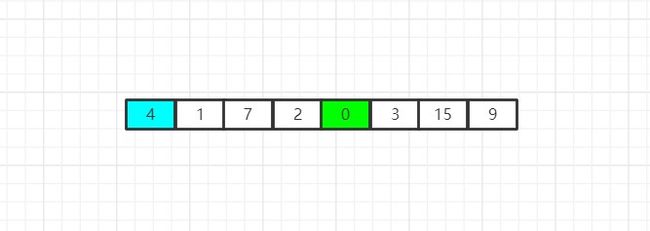
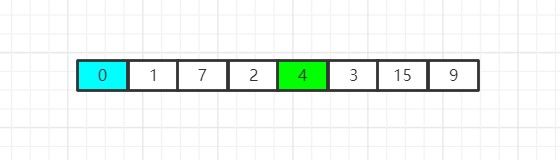
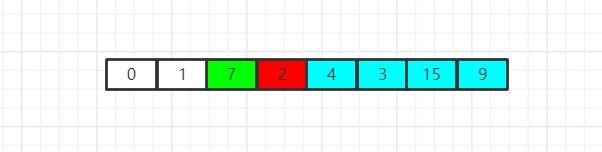
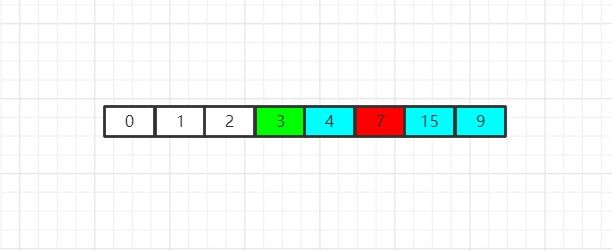
​ 如图所示，我们已经得到了一个数组，它是无序的，现在，我们开始寻找这个无序数组中的最小值(也可以寻找最大值，但是这里我们以寻找最小值为例。)，首先，我们摘到了0，我们发现0是最小值，因此我们让0和数组首位互换位置：

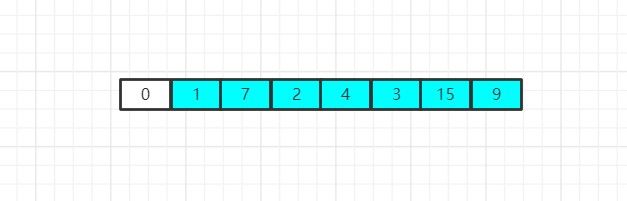
​ 之后，我们缩小数组的范围，我们从数组的第二个位置开始算起，将原数组中以下标为1的元素为首元素的子数组作为新数组(蓝色填充区域为新数组)，然后我们在这个新数组中重复刚才的取最小值并交换的行为：

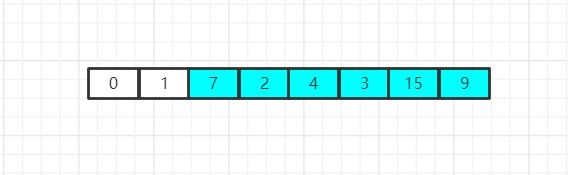
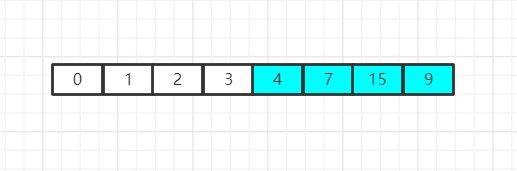
​ 现在，我们可以找到新数组中的最小值是1，因此我们将1和新数组的首元素位置进行互换，但是这里1所在的位置就是首元素位置，所以这里交换行为实际上没什么意义，之后我们再次缩小数组规模并重复检索行为：

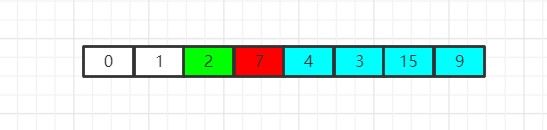
​ 现在，我们经过检索发现，2是当前新数组中的最小元素，因此我们将其和该数组的首元素进行位置互换：

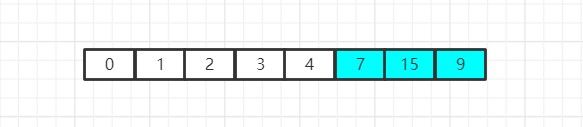
​ 之后，我们继续缩小数组规模，并重复检索行为：

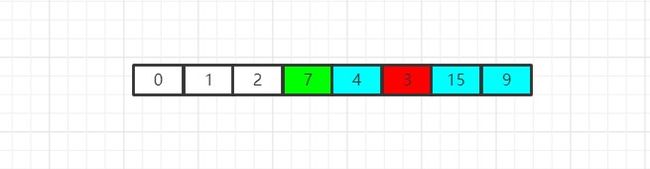
​ 我们经过检索发现，当前数组中的最小元素为3，因此我们继续将其和当前数组中的首元素进行位置互换：

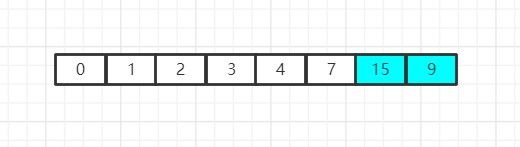
​ 现在我们继续缩小数组的规模，并继续检索：

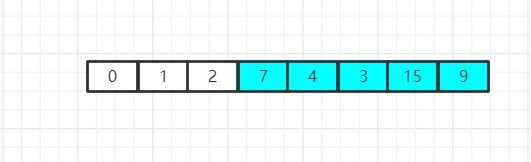
​ 经过检索我们发现，当前数组中的最小元素是4，它也恰好是首元素，因此这里交换行为没什么意义，并继续下一轮循环，缩小一次数组规模并继续检索：

​ 经过检索我们发现，当前数组中的最小元素是7，它恰好也是首节点，因此这里的交换行为同样没什么意义，在经过没有意义但是必须执行的交换之后，我们开始下一轮循环，缩小数组规模并重新开始检索：

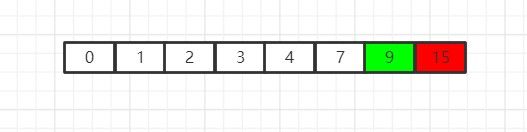
​ 在当前新数组中，我们发现最小的元素是9，我们将其哈数组的首元素进行互换：

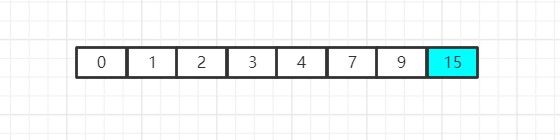
​ 之后我们继续缩小数组规模并重新进行检索：

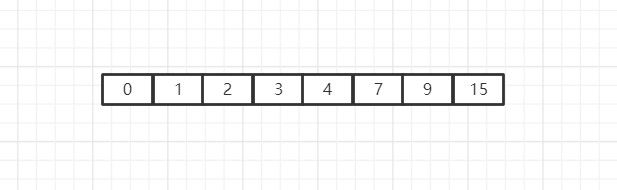
​ 然而此时我们发现，新数组中只剩下一个元素，我们已经将整个数组遍历完一遍了，因此此时整个程序就宣告结束，而这个数组，实际上也排好序了。

​ 这就是选择排序。

4.总结

​ 因此我们可以看到选择排序的原理实际上就是不断的寻找当前数组中的最小元素/最大元素，然后将他们放到最前边/最后边的位置上去，这个位置的放置是通过交换来实现的，因为它们被放置在最前/后边的位置上以后，数组就要从最前边/后边缩小一个单位，也就是不再考虑已经被排好序，放在正确位置上的那个元素了，而是要考虑剩下的元素们，通过交换，我们可以将之前数组中的最小/最大元素放到相应位置去，并把之前那个位置上的元素转移到即将要被重复这个行为的新数组中来，通过这种方法我们可以巧妙方便的在原数组上构建新数组，而不需要额外的数组空间进行结果数组的保存，也无需使用其他数组来标志哪个元素已经被排过序了这一事件，这就是选择排序的巧妙之处。

2.选择排序的代码详解

​ 接下来我们来看看选择排序算法的代码，并对代码进行详细的分析：

public static void searchSort(int[] arr){
        for (int i = 0; i<arr.length - 1; i++){//①
            int minIndex = i;
            int min = arr[i];//②
            for (int j = i + 1; j<arr.length; j++){//③
                if(min>arr[j]){
                    min = arr[j];
                    minIndex = j;
                }
            }
            arr[minIndex] = arr[i];
            arr[i] = min;//④
        }
        System.out.println(Arrays.toString(arr));
    }

​ ①.我们定义一个循环，这个循环就是用来进行上述的每轮排序行为的，在这个循环中，每轮循环都会找到当前数组中的最小值，并让这个最小值和当前数组的首元素进行位置互换。与此同时，循环头中的变量i在这里也有有着丰富的含义，它不仅代表循环的次数，它也代表着每次轮循环中数组的首元素位置，当数组中的首元素位置就是原最大的那个数组中最后一个元素的位置时，就说明排序已经到头，算法可以结束了。

​ ②.我们定义最小值的下标变量，同时定义最小值。这里主要是找最值的方法，找最值的方法一般都是默认数组首节点是最值点，然后对数组进行遍历，在遍历过程中会依次查看整个数组中的所有元素并和最值进行对比，如果发现了比最值小的元素，那么就让当前的数组元素替换掉之前的最值元素成为新的最值元素，如这里使用minIndex保存最值下标，使用min保存最值，当找到数组中新的最值时，新的最值下标就会替换掉minIndex中原来的值，而新的最值也会替换掉min中原来的值。

​ ③.这个循环就是找最值的循环体，具体解释看上文中②的解释。

​ ④.这里的两句代码就是将找到的最值与数组首元素的值进行对换的行为。之后将开启新的一轮循环，新数组将从i开始，而i这时加了1，这就代表着新数组往后“缩”了一格，规模变小了一些。重复进行外循环，直到外循环终止，这个数组最终会被排好序。

​ 以上就是选择排序法，要多加练习，才能快速的写出它。