23考研线性代数复习笔记（自用）
待补充
目录
- 一、行列式：
-
- 行列式概念和性质
- 重要行列式
- 按行（列）展开
- 行列式公式
- 克莱姆法则
- 二、矩阵
-
- 矩阵的运算
- 矩阵的逆
- 矩阵的初等变换
- 矩阵的秩
- 伴随矩阵
- 分块矩阵
- 三、向量
-
- 向量的概念及运算
- 线性组合和线性表示
- 线性相关和线性无关
- 极大线性无关组与向量组的秩
- 向量空间
- Schmidt正交化
- 四、线性方程组
-
- 方程组的表达形与解向量
- 解的判定与性质
- 基础解系
- 解的结构（通解）
- 公共解与同解
- 五、特征值与特征向量
-
- 矩阵的特征值与特征向量
- 相似矩阵
- 矩阵的相似对角化
- 实对称矩阵
- 六、二次型
-
- 二次型及其标准形
- 惯性定理及规范型
- 合同矩阵
- 正定二次型与正定矩阵
一、行列式：
行列式概念和性质
1、逆序数： 所有的逆序的总数 ；
2、行列式定义：不同行不同列元素乘积代数和 ；
3、行列式性质：（用于化简行列式）；
（1）行列互换（转置），行列式的值不变 ；
（2）两行（列）互换，行列式变号 ；
（3）提公因式：行列式的某一行（列）的所有元素都乘以同一数 k，等于用数k乘此行列式 ；
（4）拆列分配：行列式中如果某一行（列）的元素都是两组数之和，那么这个行列式就等于两个行列式之和 ；
（5）一行（列）乘k加到另一行（列），行列式的值不变 ；
（6）两行成比例，行列式的值为0 ；
重要行列式
4、上（下）三角（主对角线）行列式的值等于主对角线元素的乘积 ；
5、副对角线行列式的值等于副对角线元素的乘积乘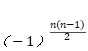 
6、Laplace展开式：（A是m阶矩阵，B是n阶矩阵），则
7、n阶（n≥2）范德蒙德行列式：
8、对角线的元素为a，其余元素为b的行列式的值：
按行（列）展开
9、按行展开定理：
（1）任一行（列）的各元素与其对应的代数余子式乘积之和等于行列式的值 ；
（2）行列式中某一行（列）各个元素与另一行（列）对应元素的代数余子式乘积之和等于 0；
行列式公式
10、行列式七大公式：
克莱姆法则
11、克莱姆法则：
二、矩阵
矩阵的运算
1、矩阵乘法注意事项：
（1）矩阵乘法要求前列后行一致；
（2）矩阵乘法不满足交换律；
（3）
2、转置的性质：
矩阵的逆
4、逆的性质：
5、逆的求法：
矩阵的初等变换
6、初等行（列）变换定义：
（1）两行（列）互换；
（2）一行（列）乘非零常数c;
（3）一行（列）乘 k加到另一行（列）;
7、初等矩阵： 单位矩阵 E经过一次初等变换得到的矩阵 ；
8、初等变换与初等矩阵的性质：
（1）初等行（列）变换相当于左（右）乘相应的初等矩阵
（2）初等矩阵均为可逆矩阵，会有
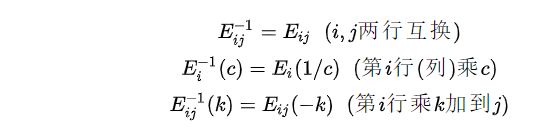
矩阵的秩
9、秩的定义： 非零子式的最高阶数；
注：
10、秩的性质：
11、秩的求法：
（1）A为抽象矩阵：由定义或性质求解；
（2）A 为数字矩阵：A阶梯型(每行第一个非零元素的下面的元素均为0),r(A)=非零行的行数;
伴随矩阵
12、伴随矩阵的性质：
分块矩阵
13、分块矩阵的乘法： 要求前列后行分法相同；
14、分块矩阵求逆：
三、向量
向量的概念及运算
线性组合和线性表示
线性相关和线性无关
8、线性相关注意事项：
9、线性相关的充要条件：
10、线性相关的充分条件：
（1）向量组含有零向量或成比例的向量必相关；
（2）部分相关，则整体相关；
（3）高维相关，则低维相关；
（4）以少表多，多必相关；
11、线性无关的充要条件
12、线性无关的充分条件：
（1）整体无关，部分无关；
（2）低维无关，高维无关；
（3）正交的非零向量组线性无关；
（4）不同特征值的特征向量无关；
13、线性相关、线性无关判定
（1）定义法；
（2）秩：若小于阶数，线性相关；若等于阶数，线性无关；
极大线性无关组与向量组的秩
14、极大线性无关组不唯一 ；
15、向量组的秩 :极大无关组中向量的个数成为向量组的秩（矩阵的秩 :非零子式的最高阶数）；
16、极大线性无关组的求法
向量空间
Schmidt正交化
（2）单位化
四、线性方程组
方程组的表达形与解向量
解的判定与性质
3、齐次方程组：
4、非齐次方程组：
5、解的性质
基础解系
6、基础解系定义：
7、重要结论：
8、基础解系的求法
解的结构（通解）
9、齐次线性方程组的通解（所有解）
10、非齐次线性方程组的通解
公共解与同解
13、重要结论
五、特征值与特征向量
矩阵的特征值与特征向量
3、重要结论：
4、特征值与特征向量的求法
5、特征方程法
6、性质
相似矩阵
矩阵的相似对角化
9、相似对角化定义：
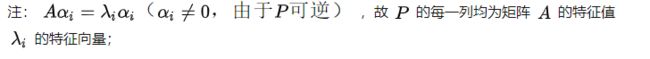
10、相似对角化的充要条件
11、相似对角化的充分条件：
12、重要结论：
实对称矩阵
13、性质
六、二次型
二次型及其标准形
1、二次型：
（1）一般形式
（2）矩阵形式（常用）：
2、标准形：如果二次型只含平方项，即
这样的二次型称为标准形（对角线）；
3、二次型化为标准形的方法：
惯性定理及规范型
4、定义：
正惯性指数：标准形中正平方项的个数称为正惯性指数，记为p；
负惯性指数：标准形中负平方项的个数称为负惯性指数，记为q；
规范型：规范型中系数1的个数等于正特征值的个数 (或二次型正惯性指数)，规范型中系数-1的个数等于负特征值的个数 (或二次型负惯性指数)。不考虑+1， -1 顺序的情况下，规范型是唯一的；
5、惯性定理： 二次型无论选取怎样的可逆线性变换为标准形，其正负惯性指数不变。
注：
（1）由于正负惯性指数不变，所以规范形唯一；
（2） p=正特征值的个数， q =负特征值的个数， p+q=非零特征值的个数 =r(A)；
合同矩阵
注：实对称矩阵相似必合同，合同必等价；
正定二次型与正定矩阵
