机器学习——卷积神经网络基础
卷积神经网络(Convolutional Neural Network:CNN)
卷积神经网络是人工神经网络的一种,是一种前馈神经网络。最早提出时的灵感来源于人类的神经元。
通俗来讲,其主要的操作就是:接受输入层的输入信息,通过卷积层,激活层,池化层,进行特征的提取与学习,然后通过全连接层完成对比,将分类结果通过输出层输出。
那么卷积神经网络最重要的任务我认为只有两个:
1.如何从原始数据中更好的学到特征信息。
2.如何将学到的特征更好的映射到标记样本。
这两个任务应该是CNN分类的关键
卷积层
对于输入层和输出层我们没什么好讲的,我们将从卷积层开始,详细了解卷积层,激活层,池化层和全连接层的详细工作原理。
CNN怎么识别
对于这个问题,我们需要引入CNN的识别原理:CNN的识别本质上是一种“局部特征”的对比,也就是说,我们将输入数据的局部与标注的样本数据的局部对比,如果某个或多个局部对比被判定为“匹配”,则认定其输入数据和样本数据属于同一类别。
朴素来讲,我们可以通过直接对图像中的像素和样本数据对比。但是这样通常过于“武断”,比如下面这种情况。
当我们选取了x图形对角线的像素对比,我们会发现并不相等,所以认定右边的图片不是x图形类别。这显然是不合适,我们需要换一种对比方法。
所以我们会选取一个“像素窗口”,截取一小块像素,把这个小块的区域成为“特征”,对比特征无误则可认定为统一类别。
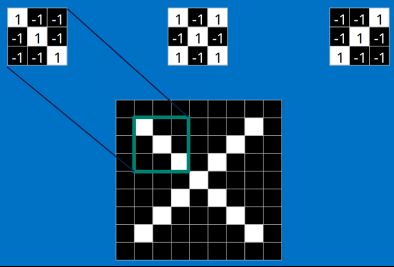
卷积层有怎么帮助CNN识别
这里我们需要明确一下这样的几个概念之间的关系
filter滤波器,这个东西实际上是卷积核的集合,而卷积核就是个权重矩阵(二维矩阵)的集合
对于一张RBG图,他的特征层分RBG三层,他通道数就是三个通道。
而且对于滤波器里的一个卷积核来说,他的二维矩阵的数量和通道数是相同的。
如下图所示,蓝色的是图片,黄色的卷积核,绿色的输出的结果(绿色的层数和卷积核的数量相同)
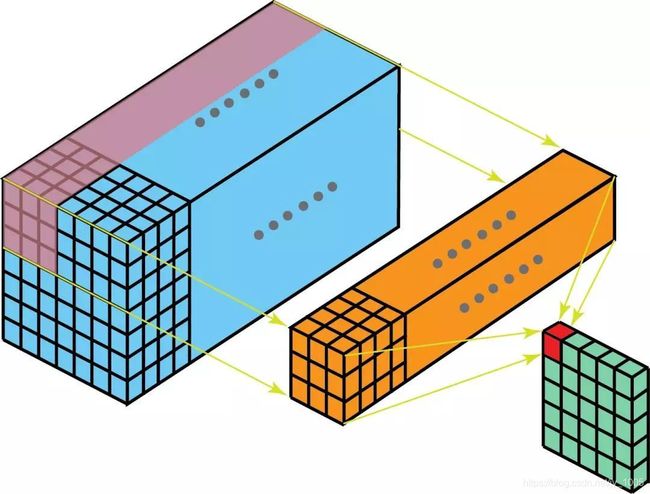
我们可以看到上面的CNN对比一个重要的点就是“特征”,卷积层可以通过算法操作,学习特征。
我们将图像视为一个三维数组,他的厚度我们称为通道数(特征层数),每一层长宽视为矩阵的大小。在这样的一层上,我们对其添加“滑动窗口”和滤波器。
然后我们通过滤波器中的各个卷积核对图像卷积(对应元素相乘后求和)得到输出矩阵,如下图。
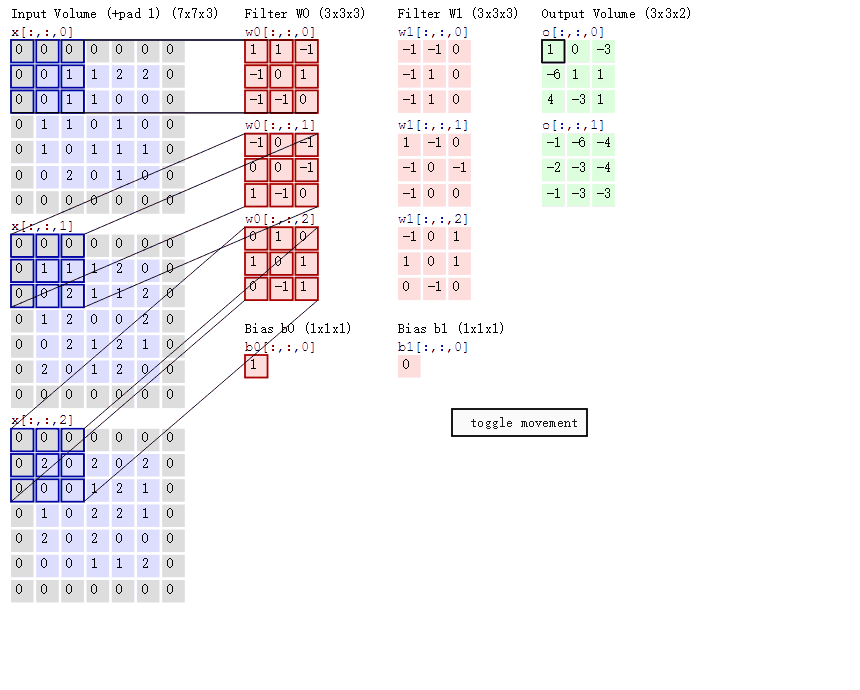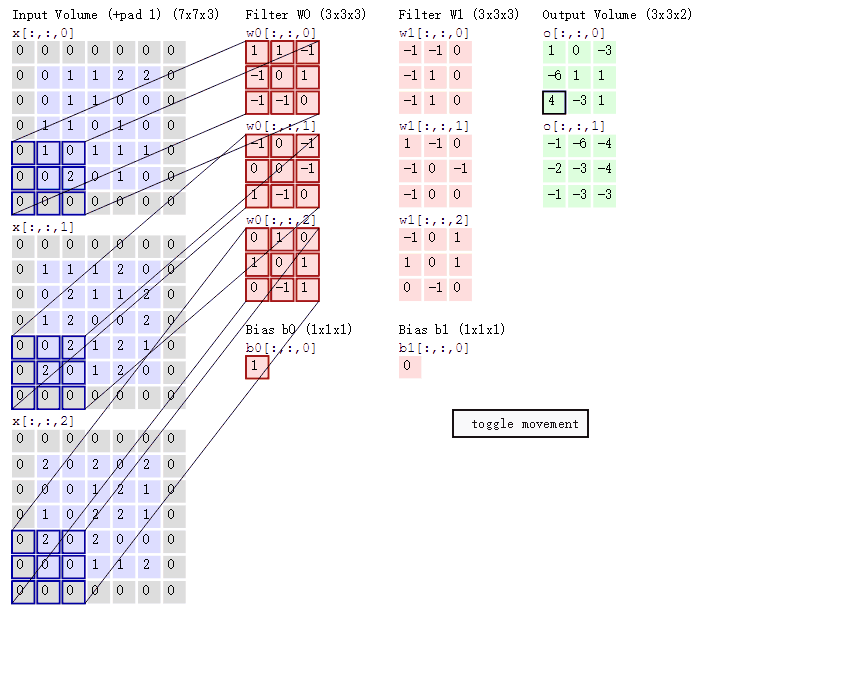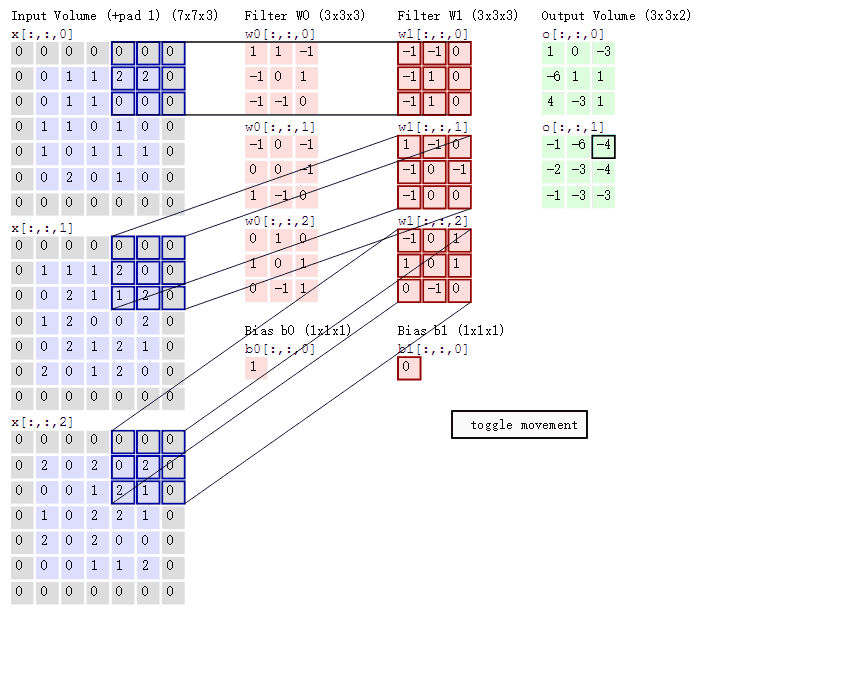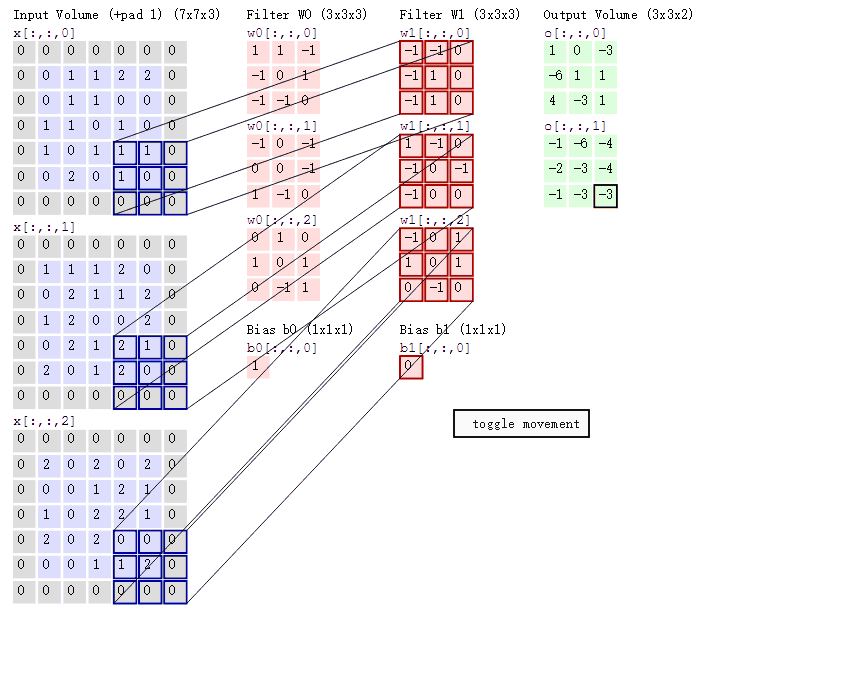
显然两个卷积核得到两个输出矩阵,三个特征层对应每个卷积核三个权重矩阵。
至此,一个卷积层的任务结束。
建议再去了解卷积核、滑动窗口这些东西具体代码的关键参数,比如卷积核的一个关键参数就是核尺寸,步幅和步数。
激活层
激活,激活什么,为什么要激活。
我理解为,激活就是激活整个神经网络的表达空间。
为什么要激活,主要还是因为仅仅靠卷积,我们没法有较好的“表达空间”,所以我们需要一个函数来帮我们把卷积层的结果做非线性映射,提升整个神经网络的表达能力。
这种函数包括:ReLU,softmax,sigmoid等。每个函数都有自身的优点,可以适用于不同场景,当然我们对一个网络可以添加多个激活层。
但是每个网络也会有自身的缺点,这些缺点无非都是偏离了激活层的初衷,让卷积层的结果没法逼近一个非线性函数来提高网络的表达能力。
PS:表达能力就可以看做学习分类能力
池化层
池化,简言之,即取区域平均或最大。
还是给定滑动窗口,但是这次只需要直接输出滑动窗口内的最大值或平均值即可,对应池化成为“最大池化”和“平均池化”。
目的是为了压缩特征,提高效率。
全连接层
建议去看这个博主的博客对全连接层(fully connected layer)的通俗理解
本质就是由一个特征空间线性变换到另一个特征空间。目标空间的任一维——也就是隐层的一个 神经元——都认为会受到源空间的每一维的影响。不考虑严谨,可以说,目标向量是源向量的加权和。
全连接层(fully connected layers,FC)在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的“分布式特征表示”(下面会讲到这个分布式特征)映射到样本标记空间的作用。在实际使用中,全连接层可由卷积操作实现:
对前层是全连接的全连接层可以转化为卷积核为1x1的卷积;而前层是卷积层的全连接层可以转化为卷积核为hw的全局卷积,hw分别为前层卷积结果的高和宽。
全连接的核心操作就是矩阵向量乘积 y = Wx


