P3938 斐波那契

题目描述

# 斐波那契

## 题目背景

大样例可在页面底部「附件」中下载。

## 题目描述

小 C 养了一些很可爱的兔子。 有一天，小 C 突然发现兔子们都是严格按照伟大的数学家斐波那契提出的模型来进行 繁衍：一对兔子从出生后第二个月起，每个月刚开始的时候都会产下一对小兔子。我们假定， 在整个过程中兔子不会出现任何意外。

小 C 把兔子按出生顺序，把兔子们从 1 开始标号，并且小 C 的兔子都是 1 号兔子和 1 号兔子的后代。如果某两对兔子是同时出生的，那么小 C 会将父母标号更小的一对优先标 号。

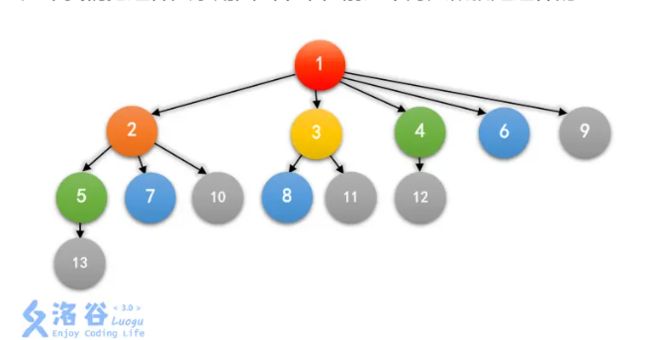
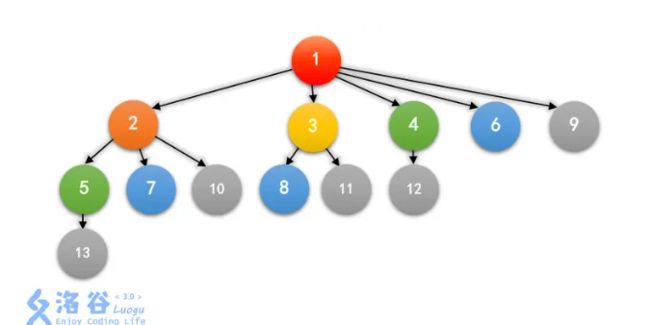
如果我们把这种关系用图画下来，前六个月大概就是这样的：

其中，一个箭头 A → B 表示 A 是 B 的祖先，相同的颜色表示同一个月出生的兔子。

为了更细致地了解兔子们是如何繁衍的，小 C 找来了一些兔子，并且向你提出了 m 个 问题：她想知道关于每两对兔子 $a_i$ 和 $b_i$ ，他们的最近公共祖先是谁。你能帮帮小 C 吗？

一对兔子的祖先是这对兔子以及他们父母（如果有的话）的祖先，而最近公共祖先是指 两对兔子所共有的祖先中，离他们的距离之和最近的一对兔子。比如，5 和 7 的最近公共祖 先是 2，1 和 2 的最近公共祖先是 1，6 和 6 的最近公共祖先是 6。

## 输入格式

从标准输入读入数据。 输入第一行，包含一个正整数 m。 输入接下来 m 行，每行包含 2 个正整数，表示 $a_i$ 和 $b_i$ 。

## 输出格式

输出到标准输出中。 输入一共 m 行，每行一个正整数，依次表示你对问题的答案。

## 样例 #1

### 样例输入 #1

```

5

1 1

2 3

5 7

7 13

4 12

```

### 样例输出 #1

```

1

1

2

2

4

```

## 提示

【数据范围与约定】 子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解 决一部分测试数据。 每个测试点的数据规模及特点如下表：

特殊性质 1：保证 $a_i$, $b_i$ 均为某一个月出生的兔子中标号最大的一对兔子。例如，对 于前六个月，标号最大的兔子分别是 1, 2, 3, 5, 8, 13。

特殊性质 2：保证 $|a_i-b_i|\le 1$。

思路

观察这个图我们发现[1],[2],[3],[4,5],[5,6,7,8],[9,10,11,12,13],也就是中括号内的都是在统一天所生出来的的，并且（做题多点）可以发现，f[1]=1，f[2]=2，f[3]=3，f[4]=5，f[5]=8（斐波那契数列，然后可以发现，对于每个中括号内的元素（同一天生的），他的父亲就是他的编号-f[当前斐波那契额数列的前一项是多少],例如,6在f[5]所包括的中括号内所以可以得到6的父亲是6-f[4]=1.....

所以对于一个查询，我们用LCA的思想，先看他们哪个编号大，谁的编号大谁先往上跳，直到他们跳到同一层为止。

代码：

#include
#define int long long
using namespace std;
const int N = 3e5+10;
const int dx[]= {0,-1,0,1,0,-1,-1,1,1};
const int dy[]= {0,0,1,0,-1,-1,1,1,-1}; 
int gcd(int a, int b){//求最大公约数
    return b ? gcd(b,a%b):a; 
}
int read(){
    int x;
    scanf("%lld",&x);
    return x;
}
int f[N];

void find (int x,int y){
    if(x>n;
    while(n--){
        int a,b;
        cin>>a>>b;
        find(a,b);
    }
}

signed main() {

    int t=1;
    // cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}