单机斗地主项目总结

好久没写博客，最近也是闲来无事，在工作业余时间写了一个斗地主的游戏，时间好像是从4月份到8月份吧，现在在来想一想，里面涉及到的一些细节好像忘的差不多了，还是写个总结吧，以祭奠我的第一款上线的手机游戏（没啥下载量的说- -#）。

 

进入正题，要总结的知识点如下：

1、屏幕适配

2、洗牌算法

3、牌面正面翻转效果所涉及的投影相关问题（参考资料http://tonybai.com/2014/05/13/sprite-draw-principles-of-cocos2dx-screen-adaptation/）

一、屏幕适配

涉及到两个分辨率的问题，一个是开发者使用的分辨率（一般背景资源的大小和此分辨率匹配），这里定义为sizeDesignResolution，还有一个就是屏幕分辨率sizeScreenResolution（就是各种不同手机的实际屏幕分辨率），这里的适配就是要用你开发的分辨率适配用户不同手机的实际屏幕分辨率。

一般产品要上线的话，你的图片是不能变形的，采取的方法可以是：

（1）等比缩放图片

（2）在充满屏幕的前提下，尽可能的减小要被截取的图片范围

等比缩放图片，要先知道用户屏幕和开发屏幕分辨率的比例因子：

float fScale_x = sizeScreenResolution.width / sizeDesignResolution.width;
float fScale_y = sizeScreenResolution.height / sizeDesignResolution.height;

这里先介绍官方的两种等比缩放的适配方案

（1）kResolutionNoBorder，采取缩放因子大的比列缩放开发分辨率，得到视口宽高

（2）kResolutionShowAll，采取缩放因子小的比列缩放开发分辨率，得到视口宽高

举例：

CCSize sizeDesignResolution = CCSizeMake(960, 540);//开发分比率

CCSize sizeScreenResolution= CCSizeMake(1024, 768);//用户分比率

比列因子

fScale_x  = 1.067

fScale_y = 1.422

 

说明fScale_x   < fScale_y 开发分辨率的高度小了；

如果采取kResolutionShowAll，得到的是宽度缩放因子，使得fScale_x = fScale_y  = 1.067，这样只是让宽度刚好得到平铺，而高度会出现黑边，可以由它的视口大小可以看出。

视口的大小

// calculate the rect of viewport    

float viewPortW = m_obDesignResolutionSize.width * m_fScaleX = 1024;

float viewPortH = m_obDesignResolutionSize.height * m_fScaleY = 576;

如果采用kResolutionNoBorder，取较大的值fScale_x = fScale_y  = 1.422，这样可以高度可以刚好铺满屏幕，这不过图片宽度会部分被截取掉

float viewPortW = m_obDesignResolutionSize.width * m_fScaleX = 1365.3334;

float viewPortH = m_obDesignResolutionSize.height * m_fScaleY = 768.00000;

其实在这种fScale_x   < fScale_y的情况下，kResolutionNoBorder适配方案可以很好的满足上面提到的这两种适配条件，但在fScale_x   > fScale_y的情况下，kResolutionShowAll也可以满足该适配条件。

综上所述，在AppDelegate.cpp中写一个综合这两种情况的判别条件处理方法，即可以达到最终的适配要求：

        //设置开发者使用的分辨率
	CCSize sizeDesignResolution = CCSizeMake(960, 540);
	CCSize sizeScreen = pEGLView->getFrameSize();
	float fScale_x = sizeScreen.width / sizeDesignResolution.width;
	float fScale_y = sizeScreen.height / sizeDesignResolution.height;
	if(fScale_x > fScale_y)//设计分辨率的高度大了，高度等比缩小
	{
		CCSize sizeResolution = CCSizeMake(sizeDesignResolution.width, sizeScreen.height / fScale_x);
		pEGLView->setDesignResolutionSize(sizeResolution.width, sizeResolution.height, kResolutionNoBorder);
	}
	else//设计分辨率的宽度大了，将其宽度等比缩小
	{
		CCSize sizeResolution = CCSizeMake(sizeScreen.width / fScale_y, sizeDesignResolution.height);
		pEGLView->setDesignResolutionSize(sizeResolution.width, sizeResolution.height, kResolutionNoBorder);
	}

这里的setDesignResolutionSize函数中的第三个参数填写kResolutionNoBorder或kResolutionShowAll都行，因为这里的宽高比列都是一样的了。
这列有一点要注意的是，在UI布局的时候，图片边界部分包含重要按钮或其他相关图片资源时，尽量写成相对坐标，这样可以保证，每个不同的机型加载的资源都会在手机上面正确显示。

二、洗牌算法

思想：

预先保留数组，含有54个元素，并由1到54依次初始化赋值；

初始化种子，并取1~54的随机数，实现下标的数组值交换，代码如下：

         #define random(X) ((rand() % (X)) + 1)
         int nLoop = 54;
         srand((unsigned int)time(0));
        
	for(int i = 1; i <= nLoop ; i++)
	{
		int rand1 = random(54);
		int rand2 = random(54);
		int temp1 = m_arrayCards[rand1];
		m_arrayCards[rand1] = m_arrayCards[rand2];
		m_arrayCards[rand2] = temp1;
	}

这里nLoop是交换的次数，此值越大，得到的牌就越离散（注：如果哪位知道更好的洗牌算法，可以告知）。

三、牌面正面翻转效果所涉及的投影相关问题

在进行牌翻转的时候，往往只有在居中的牌，在能够刚好实现正面翻转，而在其他位置的牌，翻转的时候往往存在一定的角度，达不到正面翻转牌的效果。

这样的问题涉及到了openGL中投影相关的知识。

OpenGL中涉及到的投影变换包含两种，一种是正射投影，一种是透视投影，在cocos2dx中默认的投影是透视投影，m_eProjection = kCCDirectorProjection3D;根据透视投影的特性，是以人眼的方式所展现的，符合人们的视觉习惯，所以在居中的地方，牌会刚好实现正面的翻转，因为相机（可以理解为人眼）的方向正好居中垂直朝向屏幕内，所以看到的图片翻转式正面翻转，而在其他地方的翻转会出现一定的角度偏差。（等会还侧重讲一下这个透视投影在cocos2dx中的展现原理）。

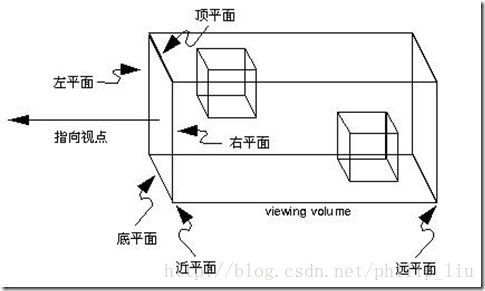
要解决这样的问题，可以先理解正射投影的特性：

它的视景体是一个平行的管道，并且无论物体距离相机多远，投影后的物体大小尺寸不变：

这样的特性刚好可以满足实现牌面正面翻转的功能，不管牌在什么位置，都相当于无数个正面照射牌位置的相机使之居中翻转显示（不知道这样解释有没有问题，因为正射投影中不需要设定照相机位置、方向以及视点的位置）。

CCDirector::sharedDirector()->setProjection(kCCDirectorProjection2D);

 

 

在CCDirect.cpp中，有getZEye(void)的函数

float CCDirector::getZEye(void)
{
    return (m_obWinSizeInPoints.height / 1.1566f);
}

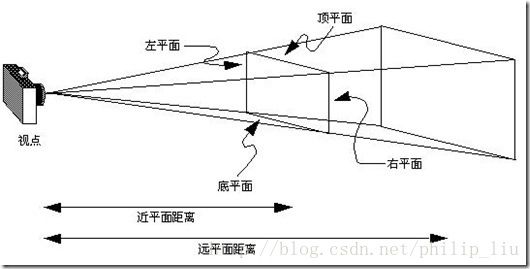
下面说说这个1.1566f是怎么来的，以这个透视图来看

cocos2dx对透视投影的设置

            float zeye = this->getZEye();

            kmMat4 matrixPerspective, matrixLookup;

            kmGLMatrixMode(KM_GL_PROJECTION);
            kmGLLoadIdentity();
            
#if CC_TARGET_PLATFORM == CC_PLATFORM_WP8
            //if needed, we need to add a rotation for Landscape orientations on Windows Phone 8 since it is always in Portrait Mode
            kmGLMultMatrix(CCEGLView::sharedOpenGLView()->getOrientationMatrix());
#endif
            // issue #1334
            kmMat4PerspectiveProjection( &matrixPerspective, 60, (GLfloat)size.width/size.height, 0.1f, zeye*2);
            // kmMat4PerspectiveProjection( &matrixPerspective, 60, (GLfloat)size.width/size.height, 0.1f, 1500);

            kmGLMultMatrix(&matrixPerspective);

            kmGLMatrixMode(KM_GL_MODELVIEW);
            kmGLLoadIdentity();
            kmVec3 eye, center, up;
            kmVec3Fill( &eye, size.width/2, size.height/2, zeye );
            kmVec3Fill( ¢center, size.width/2, size.height/2, 0.0f );
            kmVec3Fill( &up, 0.0f, 1.0f, 0.0f);
            kmMat4LookAt(&matrixLookup, &eye, ¢er, &up);

由透视投影矩阵函数kmMat4PerspectiveProjection可以知道:

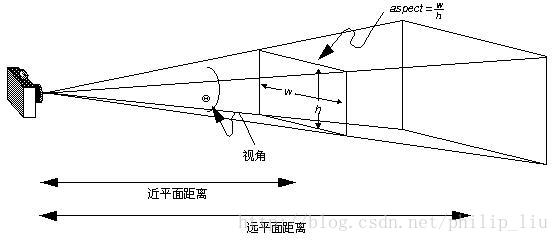
视角：60

aspect：用户分辨率的宽高比

近平面距离：0.1f

远平面距离：2*zeye

最后可以得到透视投影矩阵matrixPerspective；如果已知透视投影矩阵matrixPerspective也可以反向求的视角、宽高比等其他参数;

这里可以来看以下zEyes值的由来，先看沿着X轴负方向向zy平面投影：

很明显，这样的一个三角形式等边三角形：

cos30 = (m_obWinSizeInPoints.height / 1.1566f)/ h
h = (m_obWinSizeInPoints.height / 1.1566f)/cos30 = m_obWinSizeInPoints.height;

可以知道投影在(z=0，XY平面)的截面高度h与用户分辨率的高度相同；Cocos2d-x是2D游戏渲染引擎，针对该引擎的模型的z坐标都是0，因此模型实际上就在xy平面内，也就 是说eye与原点的距离恰好就是eye与模型的距离，而模型可显示区域的最大高度也就是h；、（但在3D游戏的渲染引擎中，eye与模型的距离不一定就是eye与原点的距离；)

 

这里知道了eye距模型的距离，但其具体的位置（x,y）还没有确定，通过上述代码可以知道，相机的位置eye（size.width/2, size.height/2, zeye），指向的位置center(size.width/2, size.height/2, 0.0f)，头顶方向的位置（0.0f, 1.0f, 0.0f），并得到模型视图矩阵matrixLookup（已知该矩阵也可以逆向推出相机的具体位置）。

 

自己对投影矩阵在三维场景中的应用的一些想法：

1、已知模型的位置

2、已知投影视图矩阵

3、已知模型视图矩阵

根据模型视图矩阵==》相机参数（位置，朝向，向上方向）

根据投影视图矩阵==》视角、宽高比

视角、eye.z==》截面高度（已知宽高比）==》截面宽度（已知eye的具体位置）==》所截取模型的矩形范围（知道这个范围，可以应用与多种实际应用中，比如影像的自动贴图，视觉范围内的影像本地保持等等云云。。。）

 

这里就大致先写到这里，后续如果有新的想法在加。

 

最后贴个斗地主游戏的下载地址，想要玩的随便下：

http://apk.hiapk.com/appinfo/com.combat.playcards