【数学建模】--因子分析模型
因子分析有斯皮尔曼在1904年首次提出,其在某种程度上可以被看成时主成分分析的推广和扩展。
因子分析法通过研究变量间的相关稀疏矩阵,把这些变量间错综复杂的关系归结成少数几个综合因子,由于归结出的因子个数少于原始变量的个数,但是它们又包含原始变量的信息,所以,这一分析过程也称为降维。由于因子往往比主成分更容易得到解释,故因子分析比主成分分析更容易成功,从而有更广泛的应用。
本讲的前面部分将简要介绍因子分析模型的数学原理,在最后的应用部分,我们将举行一个实例帮助大家理解,大家可以把重点放在最后的应用上。
因子分析和主成分分析的对比:
因子旋转:
原理及其方法的总结:因子分析是一种常用的统计分析方法,用于探索多个观测变量之间的关系,目的是找到潜在的因子或构建维度,将多个变量归纳为较少的几个潜在因子,以简化数据分析和解释。
在因子分析中,我们假设观测变量是由潜在因子所驱动,并且这些潜在因子无法直接观测到。通过因子分析,我们可以确定这些潜在因子在整个数据集中的作用程度,并且可以根据因子负载(factor loading)来衡量每个观测变量和潜在因子之间的相关性。因子负载表示观测变量与潜在因子之间的线性关系强度,取值范围通常在-1到1之间,绝对值越大表示相关性越强。
在实施因子分析时,通常包括以下步骤:
1.数据准备:收集相关观测变量的数据,确保数据的可靠性和合理性。
2.因子提取:采用不同的因子提取方法,如主成分分析(PCA)、最大似然估计法(MLE)或常见因子法(CF)等,从观测变量中提取潜在因子。
3.因子旋转:对提取得到的因子进行旋转,以使因子负载更容易解释和理解。常用的旋转方法包括正交旋转(如方差最大化旋转,如Varimax)和斜交旋转(如极大似然估计法,如Promax)等。
4.因子解释和命名:根据因子负载和变量之间的关系,解释提取得到的因子,并为这些因子命名,以便更好地理解其意义。
5.结果解释和使用:基于因子分析的结果,可以进行进一步的数据分析、模型构建或决策制定。
需要注意的是,因子分析是一种探索性分析方法,其结果依赖于数据的质量和所选择的分析方法。因此,在实施因子分析时,应当谨慎选择因子的提取和旋转方法,并结合领域知识和实际情况进行合理解释和使用。
因子分析的实例以及Spss操作:
步骤:
一:将数据导入到Spss中,观察是否能通过检验,若能通过检验,再跟据碎石图确定因子数目。
二:得到因子数目后,再在、重新用spss分析一遍,与第一次不同,第二次的分析中要输入确定的因子数目: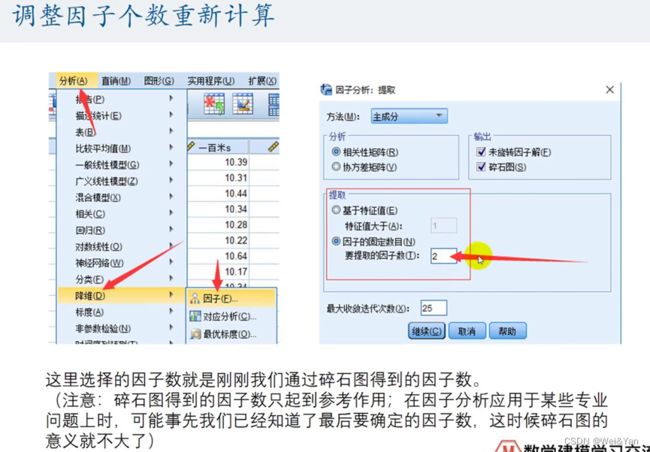
三:在因子分析的结果分析中,主要关注以下几个重要指标和步骤:
1.因子载荷(Factor Loadings):因子载荷表示每个变量与因子之间的关系强度,它衡量了变量与因子之间的相关性。载荷通常介于-1和1之间,越接近于1表示变量与因子之间的相关性越强。在结果分析中,可以查看载荷矩阵,找出高载荷的变量与对应的因子,以解释因子结构。
2.特征值(Eigenvalues):特征值衡量了每个因子解释的总方差量。较高的特征值表示该因子解释了较大的方差比例。通常,选择特征值大于1的因子作为解释因子结构的依据。
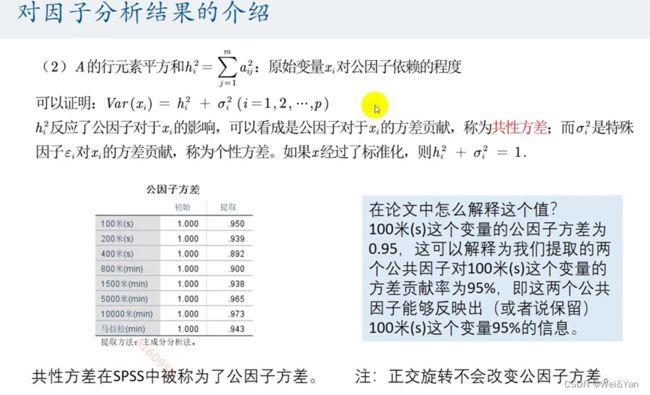
3.解释方差(Explained Variance):解释方差指示了因子分析所提取的因子结构能够解释原始变量方差的百分比。可以通过查看累积解释方差来确定所选因子的总体解释能力。
4.因子旋转(Factor Rotation):在因子分析中,旋转可以改善因子的解释性和解释可行性。常用的旋转方法有正交旋转(如Varimax)和斜交旋转(如Promax)。旋转后的因子载荷矩阵更易解释,因此对解释因子结构非常有用。
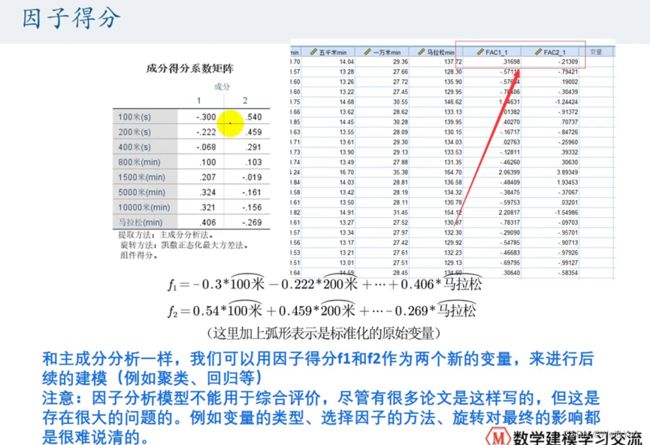
5.因子得分(Factor Scores):通过因子得分,可以将每个观测单位在因子上的得分进行计算,从而对观测单位进行分类、聚类或描述性分析。
综合以上指标和步骤,可以对因子分析的结果进行分析描述。可以考虑以下方面:
1.解释因子结构:根据载荷矩阵和特征值,确定每个因子与哪些变量具有高相关性,以解释潜在的潜在结构。比较载荷值,观察哪些变量对哪个因子有更大的贡献。
2.确定因子数量和命名:根据特征值、解释方差和理论知识,确定提取的因子数量。为每个因子命名,根据变量载荷的模式和内容,寻找共性的主题或潜在构念。
3.解释因子的含义:解释每个因子所代表的潜在构念或主题。通过观察每个因子的高载荷变量和变量的意义,可以确定每个因子所代表的特定概念。
4.解释解释方差:根据解释方差,确定选择的因子能够解释原始数据中的方差比例。较高的解释方差表示所提取的因子结构具有较强的解释能力。
5.解释因子得分:根据观测单位在因子上的得分,解释不同观测单位在每个因子上的特点和趋势。根据得分情况,可以对观测单位进行分类、聚类或描述性分析。
这些步骤和指标可以帮助您理解和描述因子分析的结果,从而更好地解释数据中的潜在结构和关系。
对于步骤1中spss的一些名词解释,检验标准和如何通过碎石图确定因子数目。
检验:
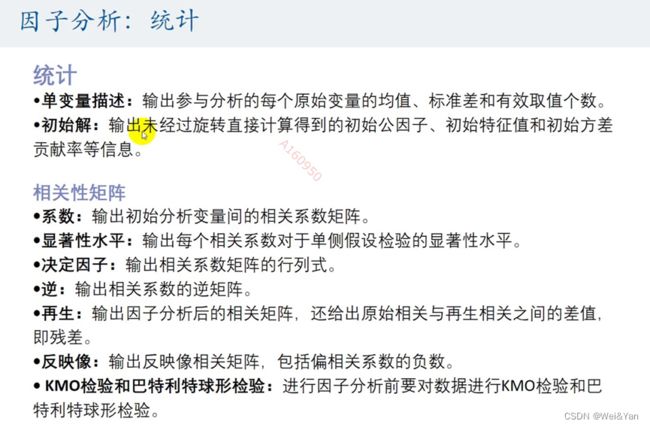
通过观察spss生成的KMO和巴特利检验观察-
如果KOM>0.9-非常适合;0.8~0,9-适合;0,7~0.8-一般,0.7以下的不适合。
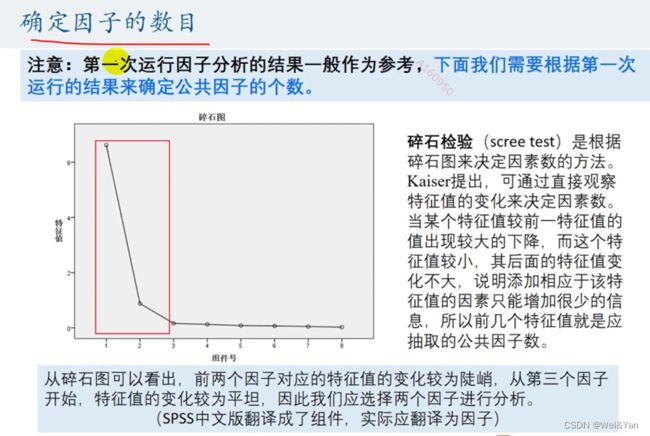
确定因子的数目:
观察图形的陡峭程度,哪些变量部分陡峭,就将变量的数目确定为因子数目。