Reinforcement Learning with Code【Code 5. Policy Gradient Methods】

Reinforcement Learning with Code【Code 5. Policy Gradient Methods】

This note records how the author begin to learn RL. Both theoretical understanding and code practice are presented. Many material are referenced such as ZhaoShiyu’s Mathematical Foundation of Reinforcement Learning, .

1. Policy Gradient 回顾

之前介绍的 Q-learning、DQN 及 DQN 改进算法都是基于价值（value-based）的方法，其中 Q-learning 是处理有限状态的算法，而 DQN 可以用来解决连续状态的问题。在强化学习中，除了基于值函数的方法，还有一支非常经典的方法，那就是基于策略（policy-based）的方法。对比两者，基于值函数的方法主要是学习值函数，然后根据值函数导出一个策略，学习过程中并不存在一个显式的策略；而基于策略的方法则是直接显式地学习一个目标策略。策略梯度是基于策略的方法的基础，本章从策略梯度算法说起。

由之前的学习参考Reinforcement Learning with Code 【Chapter 9. Policy Gradient Methods】，可以策略梯度有三个metric可以使用，分别是平均状态值（average state value），平均奖励（average reward）和从特定状态出发的平均状态值（state value of a specific starting state）。其中使用最多就是从特定状态出发的平均状态值，记为$v_{\pi }(s_0)$，其中$s_0$表示初始状态。所有当我们使用从特点状态出发的平均状态值（state value of a specific starting state）作为优化目标函数的时候，我们的待优化函数可以写作
$$\underset{\theta }{\max }J(\theta )=\mathbb{E}[v_{{\pi }_{\theta }}(s_0)]$$
再根据策略梯度定理，则有证明略（可以参考Hands on RL)
$${\nabla }_{\theta }J(\theta )=\mathbb{E}[{\nabla }_{\theta }\ln \pi (A|S;\theta )q_{\pi }(S,A)]$$
这一梯度更新法则是不能使用的，这是因为$q_{\pi }(S,A)$是真值，我们不能获得，我们可以借助Monte-Carlo的思想来对此进行更新，用一个episode的return来代替这个Q-value，即
$$q_{\pi }(s_t,a_t)=\sum _{k=t+1}^T{\gamma }^{k-t-1}{r}_k$$
那我们获得的梯度更新法则为
$${\nabla }_{\theta }J(\theta )=\mathbb{E}[{\nabla }_{\theta }\ln \pi (A|S;\theta )\times \sum _{k=t+1}^T{\gamma }^{k-t-1}{r}_k)]$$
还原出待优化的目标函数即为
$$\underset{\theta }{\max }J(\theta )=\mathbb{E}[\ln \pi (A|S;\theta )\times \sum _{k=t+1}^T{\gamma }^{k-t-1}{r}_k)]$$
这个应用了Monte-Carlo思想的算法又被称为REINFORCE。

2. Policy Gradient Code

智能体的交互环境采用的是gym的CartPole-v1环境，已经在中Reinforcement Learning with Code 【Code 4. Vanilla DQN】进行过介绍，此处不再赘述。

import gym
import torch
import torch.nn as nn
import torch.nn.functional as F
from tqdm import tqdm
import matplotlib.pyplot as plt
import numpy as np

# Define the policy network
class PolicyNet(nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(PolicyNet, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, action_dim)

    def forward(self, observation):
        x = F.relu(self.fc1(observation))
        x = F.softmax(self.fc2(x), dim=1)
        return x


# Implement REINFORCE algorithm
class REINFORCE():
    def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma, device):
        self.policy_net = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
        self.optimizer = torch.optim.Adam(self.policy_net.parameters(), lr=learning_rate)
        self.gamma = gamma
        self.device = device
    
    def choose_action(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        probs = self.policy_net(state)
        action_probs_dist = torch.distributions.Categorical(probs)    # generate prob distribution according to probs
        action = action_probs_dist.sample().item()
        return action
    
    def learn(self, transition_dict):
        reward_list = transition_dict['rewards']
        state_list = transition_dict['states']
        action_list = transition_dict['actions']

        G = 0
        self.optimizer.zero_grad()
        for i in reversed(range(len(reward_list))):
            reward = reward_list[i]
            state = torch.tensor([state_list[i]], dtype=torch.float).to(self.device)
            action = torch.tensor([action_list[i]]).view(-1,1).to(self.device)
            log_prob = torch.log(self.policy_net(state).gather(dim=1,index=action))
            G = self.gamma * G + reward
            loss = -log_prob * G    # 计算每一步的损失函数，有负号是因为我们需要max这个loss
            loss.backward()     # 反向传播累计梯度
        self.optimizer.step()   # after one episode 梯度更新


def train_policy_net_agent(env, agent, num_episodes, seed):
    return_list = []
    for i in range(10):
        with tqdm(total = int(num_episodes/10), desc="Iteration %d"%(i+1)) as pbar:
            for i_episode in range(int(num_episodes/10)):
                episode_return = 0
                transition_dict = {
                    'states': [],
                    'actions': [],
                    'next_states': [],
                    'rewards': [],
                    'dones': []
                }
                observation, _ = env.reset(seed=seed)
                done = False
                while not done:
                    if render:
                        env.render()
                    action = agent.choose_action(observation)
                    observation_, reward, terminated, truncated, _ = env.step(action)
                    done = terminated or truncated
                    # save one episode experience into a dict
                    transition_dict['states'].append(observation)
                    transition_dict['actions'].append(action)
                    transition_dict['next_states'].append(observation_)
                    transition_dict['rewards'].append(reward)
                    transition_dict['dones'].append(done)
                    # swap state
                    observation = observation_
                    # compute one episode return
                    episode_return += reward
                return_list.append(episode_return)
                agent.learn(transition_dict)
                if((i_episode + 1) % 10 == 0):
                    pbar.set_postfix({
                        'episode': '%d'%(num_episodes / 10 * i + i_episode + 1),
                        'return': '%.3f'%(np.mean(return_list[-10:]))
                    })
                pbar.update(1)
    env.close()
    return return_list

def moving_average(a, window_size):
    cumulative_sum = np.cumsum(np.insert(a, 0, 0)) 
    middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
    r = np.arange(1, window_size-1, 2)
    begin = np.cumsum(a[:window_size-1])[::2] / r
    end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
    return np.concatenate((begin, middle, end))

def plot_curve(return_list, mv_return, algorithm_name, env_name):
    episodes_list = list(range(len(return_list)))
    plt.plot(episodes_list, return_list, c='gray', alpha=0.6)
    plt.plot(episodes_list, mv_return)
    plt.xlabel('Episodes')
    plt.ylabel('Returns')
    plt.title('{} on {}'.format(algorithm_name, env_name))
    plt.show()

if __name__=="__main__":
    learning_rate = 1e-3    # learning rate
    num_episodes = 1000     # episodes length
    hidden_dim = 128        # hidden layers dimension
    gamma = 0.98            # discounted rate
    device = torch.device('cuda' if torch.cuda.is_available() else 'gpu')

    env_name = 'CartPole-v1'    # gym env name  
    render = False              # render or not

    # reproducible
    seed_number = 0
    torch.manual_seed(seed_number)
    np.random.seed(seed_number)


    if render:
        env = gym.make(id=env_name, render_mode='human')
    else:
        env = gym.make(id=env_name, render_mode=None)
    state_dim = env.observation_space.shape[0]
    action_dim = env.action_space.n

    agent = REINFORCE(state_dim, hidden_dim, action_dim, learning_rate, gamma, device)
    return_list = train_policy_net_agent(env, agent, num_episodes, seed_number)

    mv_return = moving_average(return_list, 9)
    plot_curve(return_list, mv_return, 'REINFORCE', env_name)

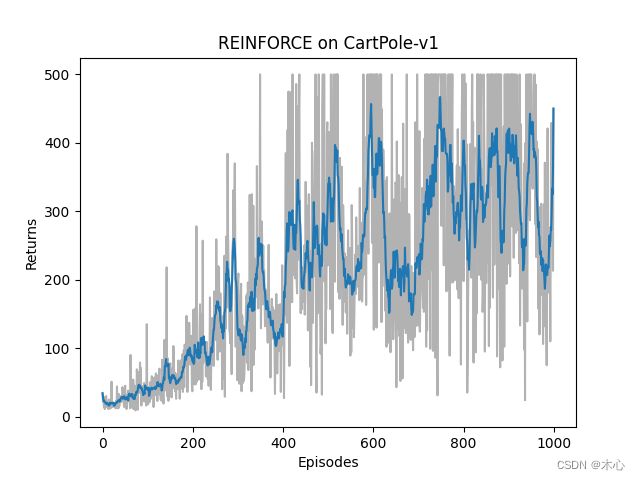
REINFORCE的效果如下图所示

---

Reference

赵世钰老师的课程
Reinforcement Learning with Code 【Chapter 9. Policy Gradient Methods】
Hands on RL
Reinforcement Learning with Code 【Code 4. Vanilla DQN】