论文阅读：《Modeling Road User Response Timing in Naturalistic Traffic Conflicts: A surprise-based framew》

  论文全名：《Modeling Road User Response Timing in Naturalistic Traffic Conflicts: A surprise-based framework》

  这篇文章讲的就是waymo在做自动驾驶安全测试中所使用的NIEON模型，那篇文章我也看了，在这里。值得仔细研读。

1 背景

  说是目前啊，在跨一系列“自然交通冲突类型”中，没有一个好办法去评估“人类反应时间”。在自动驾驶系统中（ADS），“反应时间模型”的只要应用包括：ADS响应性能的基准测试、以及在仿真测试中建模其他Agent如何响应ADS。如果找到一个好方法能得到“人类反应时间”，那这个方法就可以作为ADS的一个benchmark，用来评估无人车性能的好坏。

  这篇文章主要是提出了一个“行为参考模型”，这个行为参考模型代表“无障碍且一直关注于道路冲突的人”的响应时间。这个模型叫NIEON，它主要关注的就是这个面对交通冲突时候的响应时间。而关于具体的避撞行为则不予考虑，这种同样属于比较复杂的主题。这个响应时间的建模方式基于这样一个思想：belief updating driven by surprising evidence。直观上理解意思应该是，人对这个conflict确实可能导致碰撞的一个信念更新过程。

  另外对于这个交通冲突（traffic conflict），具体的定义为：a situation where two or more conflict partners approach each other in time and space to such extent that a crash is imminent if their movements remain unchanged。就是说，两个及以上的冲突方在时空上互相接近，如果他们不改变行为，那即将就会发生碰撞。

2 响应时间的测量与建模（in the wild）

2.1 传统的“感知-响应时间”概念及其局限性

  了解一下传统方法，知道方法演变过程对于理解也是很重要的~

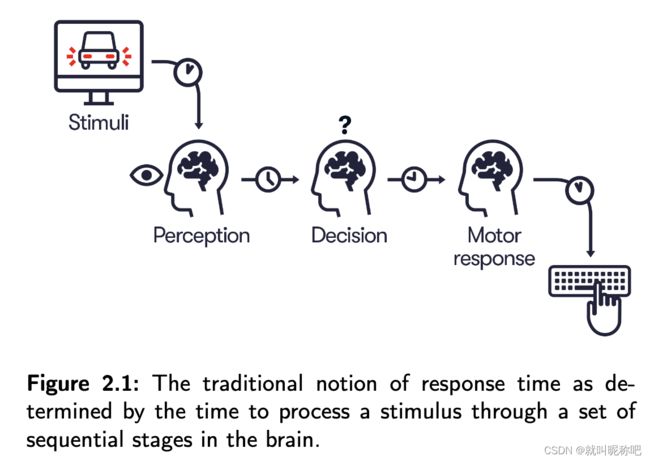
  传统方法从响应过程的概念出发，把响应过程划分为一系列信息处理阶段：检测、识别、决策、响应。大脑去执行这一过程的耗时就称为感知-响应时间（perception-response time， PRT）。看下面这个图，PRT 通常可以概念化为在大脑的一系列处理阶段中处理一个明确的刺激所需的时间。所以这个PRT一般都被视作为个体的特质。

  这个建模方式应用在自然的交通场景下是有问题的：

1. 响应过程强依赖于场景（大量的研究工作已经证实了情景运动学和响应时间存在密切的联系，无论是在自然数据下还是在控制实验下），所以响应时间不能只看脑子里的处理过程。
2. 缺少一个规范的，可推广的方法去定义“刺激”。因为在自然环境下，我们不知道怎么去定义道路使用者应该在什么样的刺激下做出反应。以及，他们是否会做出反应取决于他们对形势发展的预期。

2.2 道路使用者响应时间建模框架（in the wild）

  这个方法的核心思想是：道路使用者对交通事件的反应可以概念化为一个推理过程， the agent’s behavior is initially guided by prior beliefs about the causes of sensory input, which are continuously updated to posterior beliefs based on the accumulation of new evidence.这个Agent的行为以一个最初的“信念”开始，然后通过观测证据的累积去不断更新这个“信念”。这里只是用贝叶斯统计的概念去解释这个概念，具体的更新过程倒是不必遵循贝叶斯那一套。

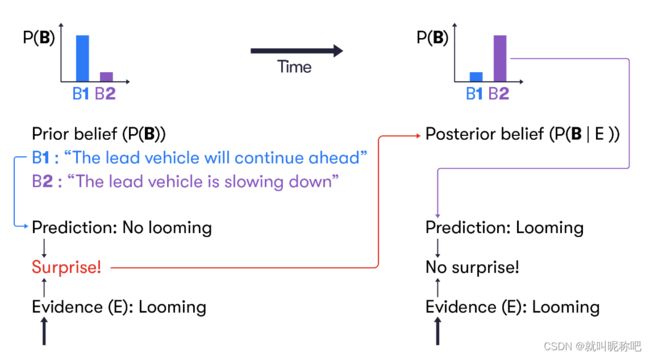
  来看一下上面这个图，它大致阐述了这个“信念更新”的过程。一车在前，后面跟车，后车接收到了与前车是否距离过近的证据。这个“证据”包括刹车灯亮起、跟车过近。在上面这部分，后车的初始“信念”就是前车会减速，然后他接收到的证据和预期相符，在这种情况下，后验的信念和初始的是一样的，信念不会更新，后续后车的减速行为也是积极主动的，毕竟这个场景一点儿都不“suprise”，也不涉及什么前车行为导致的响应。然后我们再看这个图的下半部分，如果后车初始的“信念”是继续往前走，那么当他后面看到刹车灯亮起时就会收到与预期不符的“证据”，在不紧急的情况下，“信念”会做一次更新，如果情况紧急，“信念”更新会有即刻的行为，比如刹车去避撞。

  “信念”这个词，换成形式化地描述，我们应该使用概率分布，所以看下上面这个图，就上述讨论的第二个例子进行一些形式化的描述。

1. 令随机变量$B$表示前车的行为，则初始“信念”的概率分布如左上角$P(B)$，$B_1$代表前车继续前行，$B_2$是前车会减速。这个例子中后车的初始信念认为前车是会继续前进的。
2. 然后前车的减速$E$被后车观测到，suprise，这时候后验“信念”变成了关于$E$的条件概率$P(B|E)$

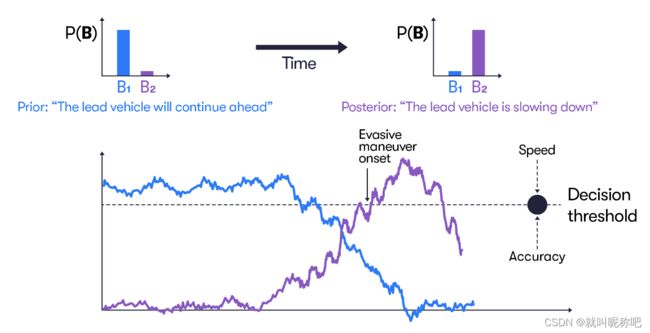
  这个框架便是前文提到的信念更新过程，道路使用者的响应时间可以根据这个框架去理解。如下图所示，一旦后验“信念”达到一定阈值，道路使用者就要开始做规避行为，这个阈值是由速度和准确性权衡来的。如果阈值设定过低，Agent很有可能很快反应，导致在即便不需要反应的情景过度反应；反之，过高阈值会导致响应过晚。

  影响道路使用者的响应时间的因素包含内部因素，比如自身的驾驶经验；外部因素比如说路况遮挡、光线等。那么这些因素在这些框架里可以以一种统一的方式去建模：影响“信念”更新进程的速度。

2.3 ADS响应时间benchmark的启发式模型实践方法

  这一小节主要描述的是一种启发式的实现方法，主要是基于人工标注的刺激。

1. 首先人工标注刺激开始时间$T_1$，是观测到suprise证据的时间，也就是说这个时就是Agent观测到违背初始信念的证据的时间点。
2. 其次是第二个刺激结束时间$T_2$，它代表信念更新完毕，并且后验和证据匹配的时间点，并且这个点会开始进行规避动作Evasive Maneuver（EM）。

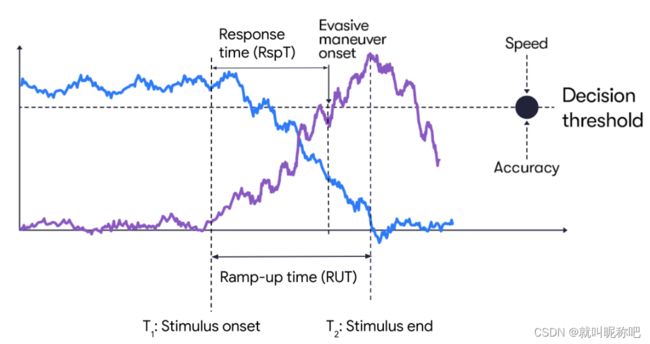
那么，$T_1$到$T_2$时间段内的差值可以用作估计suprise证据积累的速率，这一段时间论文给它取了个名字叫 ramp-up time（RUT），如下图所示。通过拟合一个统计模型，响应时间RspT可以在一个新的场景中通过$RUT$预测出来。

  像$T_1,T_2,EM$这些都在自然碰撞数据库中标注出来了，用的时候可以把$RUT$作为$x$，把$RspT=EM-T_1$作为$y$，去拟合个模型作预测。

3 方法

  上一节描述的启发式算法用于建模SHRP2自然碰撞数据集中追尾（Rear-end）场景的响应时间。这一节主要用于描述获取、选择、标注自然驾驶数据的方法。

3.1 Rear-end冲突场景定义

  这里我们用$LV$代表前车，$SV$代表后车，Rear-end冲突场景主要分为三种类型：

• $S_1$：$LV$突然刹车，$SV$尾随其后
• $S_2$：$LV$向车道外移动，$SV$尾随其后
• $S_3$：$LV$停止或缓慢移动，$SV$从后面靠近

3.2 自然驾驶数据

  这里用到的自然冲突数据来自SHRP2（Strategic Highway Re-search Program 2）。这个数据库是公开的，值得看一下。由Virginia Tech Transportation Institute (VTTI)维护。

3.3 可见的跟车过近计算（Visual looming computation）

  上面讨论的$T_1,T_2$怎么标注，就依赖于这个visual looming，这里给出它的定义：the optical expansion of the lead vehicle, typically operationalized as the rate of change of the angle,, that an object subtends on the subject’s retina。前车在后面驾驶员视网膜上的光学角度$\theta$的膨胀率。看下面这个图，感觉就是$\theta$的变化率。$\theta$是直接从SHRP2视频里半手工提取的。

  前车宽度这方面，作者开发了一个计算机视觉方法来跟踪前车的左右角，前车宽度是以图像像素为单位估计的，根据 SHRP2相机的有效像素数和计算机视觉算法使用的调整像素宽度，使用720/500的转换因子将其转换为毫米。然后$\theta$就可以计算为：

$$\theta =2\ast arctan(\frac{w/2}{c_{fl}})$$

其中$w$是前车在图像内的宽度，$c_{fl}=3.6mm$是SHRP2前置相机的焦距。

3.4 数据标注

  对于上述三种追尾类型场景，下面以$S_1$为例去描述这个数据标注的方式。

  $SV$跟车$LV$，$LV$突然减速。这里对于$SV$来说，初始信念，我们用$H_i$来表示，代表$LV$会以恒定速度或恒定加速度继续前进；后验信念，我们用$H_a$来表示，代表$LV$刹车并且$SV$需要立即开始做出动作规避碰撞。那么$T_1$就由以下两个事件先发生的那个来决定：

1. 前车的刹车灯第一次突然亮起的时间
2. 对于$SV$司机，肉眼可见$LV$减速的时间

那么，对于刹车灯亮起的情况，有些情况不是那么suprise，比如说前面排队，或者到红灯。还有一些情况前车刹车灯一直亮着，比如说在下坡。那么在这些情况下，$T_1$就只能通过上面第二个事件来决定了。

  $T_2$的决定方式为：$T_1$时间点后，$\theta$的膨胀率达到一定阈值（$0.05rad/s$）的时候。如果$T_1$就达到这个阈值了，那$T_2=T_1$。这个阈值是可调整权衡的。

  $EM$，规避动作开始，是通过加速度序列去看的，因为SHRP2里面不包含踩刹车的输入。比如说，$SV$在以恒定的较低的减速度开车时，$EM$就被标注为$SV$减速度突然增大的那个时间点。$EM$发生在VTTI标注的subjective reaction之后（这个东西应该是数据提供的）

  eyes-off-path，这个布尔值变量是通过VTTI eyeglance数据标注的。在$T_1$时刻和subjective reaction之间，如果$SV$司机瞥了一眼距离前方道路比较远的地方，这个eyes-off-path就设置为True。我理解，因为之前提到过，NIEON模型代表的是时刻关注道路冲突的司机，所以眼睛就不能往别地方看。

  以上$T_1,T_2,EM$和eyes-off-path，这四个量基本上就是这么标注的，当然还有一些细节需要注意。

3.5 数据采样方法

  这一节主要描述对SHRP2数据的采样方法。

  首先用incident_type = Rear-end, striking这个字段过滤追尾场景。然后应用以下4条准则去筛选具体的事件：

1. $trafficconflict$：事件是否能被算作交通冲突，是看车在受到刺激时，是否刹车比平时狠“harder than usual”
2. $Stimulusonsetvisibility$：刺激时间$T_1$发生在车的前置摄像机视野范围内，不能被雾或黑暗遮挡
3. $Videoexistsandisofadequatequality$：视频质量可以获得$T_1$，以及可运行计算机视觉算法
4. $Truerear-endscenario$：如果$LV$变道或转弯离开$SV$车道，车道偏移不超过50%

  然后只有eyes-off-path=False的事件会被留下来。

4 结果

4.1 响应时间分布和响应模型拟合

  这些采样出来的事件，得到的响应时间分布如下图所示。

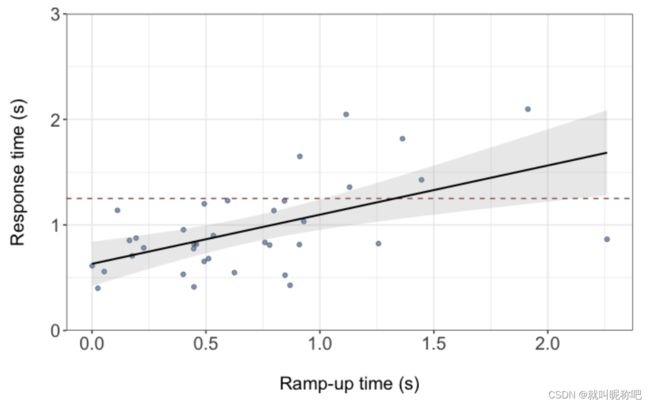
数据表现出长尾效应，但是与预期相符的是，ramp-up time和响应时间的皮尔逊相关系数达到0.55。如下图所示。

为了便于解释，waymo拟合了个线性模型，虽然还可以通过更好的方式去拟合。上面红色线是另外一篇论文在追尾冲突下设定的“规范响应时间1.25s”。灰色部分是95%置信区间。

$$RspT=0.63+0.47\ast RUT$$

4.2 对实验响应时间数据的验证

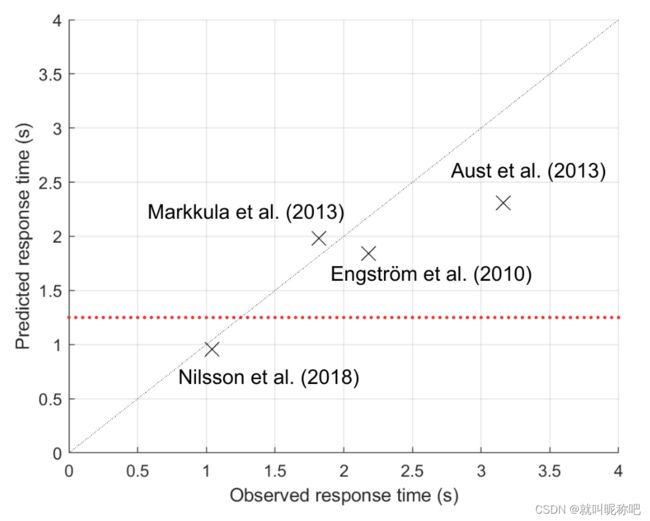
  为了去验证这个模型，本文还去和别的工作做出的响应时间进行了对比。如上图和表所示。可以看到这些相关工作观察到的响应时间区别很大，这很大程度上就是场景动力学差异导致的，特别是初始时间差异（上面表里的Init time gap），以及$LV$的减速度大小。表里Nilsson的工作，初始时间最小，$LV$减速度最大，得到的响应时间也最小1.04s。

  另外，看上面这个图，本文的模型也较好地预测了这四个研究工作。模型的拟合效果通过下边这个式子评估：

$$R^2=1-\frac{{\sum }_{k=1}^n(p_k-o_k^2)}{{\sum }_{k=1}^n(o_k-\overline{o})}$$

其中，$k=1,\cdots ,N(N=4)$，代表4个研究工作。$o_k$是观测到的平均响应时间，$p_k$是模型预测的平均响应时间，$\overline{o}$是4个研究工作平均响应时间的平均数。$R^2=0.62$，表示模型解释了来自4个研究工作的平均响应时间的62%的方差。

  这些研究工作表明：

• 人类的反应时间强依赖于情境
• 本文的NIEON模型捕捉到了这种依赖关系，并且较好地推广到了未知的响应时间数据

5 一种框架计算实现方式

  这一节讲述了一种这个框架的计算实现方式，主要还是以统计机器学习为主的方法，另外还有一个“证据累积框架”（evidence accumulate framework），引用的其他论文相关工作。这一节设计到的前人工作较多，值得后续深入再看看。

附录

  附录里面介绍了一些方法细节，了解一下，需要时可回来再细看。

• 附录A讲了上述研究的三个追尾场景的方法细节，包括标注方法，和特殊情况讨论。
• 附录B讲了一下这个模型怎么推广到其他类型场景
• 附录C讲了文中计算机视觉方法，用的OpenCV

总结（个人）

  这篇文章前前后后的工作量可以看出是非常巨大的，文章主要讲了在追尾场景下，人类的反应应该怎样怎样的，得到的结果有助于去证明ADS在安全方面比人类开得要好。同时这篇文章的思路或许也可以推广到自动驾驶其他维度与人类的对比，比如说乘车舒适度等。

  另外对于大规模的落地应用，第五章框架计算方式是值得去深入研究的，该章节参考了很多很多相关工作，需要持续钻研。