数制与码制

用0和1可以组成二进制数表示是数量的大小，也可以表示对立的两种逻辑状态。数字系统中常用二进制数来表示数值。

       在微处理器、计算机和数据通信中，采用十六进制。任意一种格式的数可以在十六、二和十进制之间相互转换。

       二进制数有加、减、乘、除四种运算，加法是各种运算的基础。特殊二进制码常用来表示10进制数。如8421码、2421码、5421码、余三码、余三码循环码、格雷码、ASCII等。

数制

我们常见的数字是十进制，而计算机中，常常会接触到二进制、八进制、十六进制，而这三种进制的转换较简单，若是进行除以上进制外的其他进制的表达，一般先转换为十进制数，再根据计算进制数的计算原理计算所需的进制。

常见进制的表示

（注意下标或前缀）

二进制的优点：

（1）易于电路表达— 0、1两个值，可以用管子的导通或截止，灯泡的亮或灭、继电器触点的闭合或断开来表示。

（2）二进制数字装置所用元件少，电路简单、可靠 。

（3）基本运算规则简单, 运算操作方便。

十六进制的优点：

    1）与二进制之间的转换容易；

2）计数容量较其它进制都大。假如同样采用四位数码。

3）书写简洁。

原码、反码、补码

补码或反码的最高位为符号位，正数为0，负数为1。

当二进制数为正数时，其补码、反码与原码相同。

当二进制数为负数时，将原码的数值位逐位求反，然后在最低位加1得到补码。

即

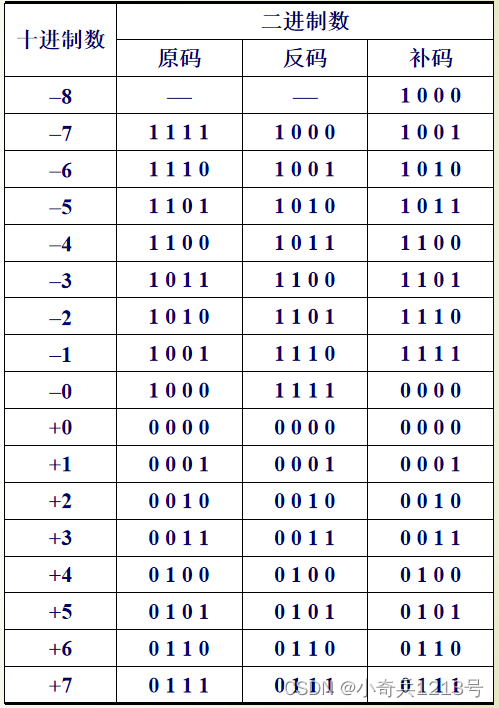
 4位二进制原码、反码、补码对照表

 n位带符号二进制数的原码、反码和补码的数值范围 :

 

二进制数的算数运算

对无符号数，则机器字长的所有位都参与表示数值。

l  对有符号数，则要留出机器字长的最高位作为符号位，其余表示数值。

无符号二进制数的算术运算

无符号二进制的加法规则： 0+0=0，0+1=1，1+1=10。

计算两个二进制数1010和0101的和

 

无符号二进制数的减法规则：0-0=0， 1-1=0，1-0=1   0-1=11

计算两个二进制数1010和0101的差

 

 

无符号二进制的乘法规则：0×0=0，0×1=0，1×0=0 ，1×1=1 。

计算两个二进制数1010和0011的积。

 

无符号二进制的除法规则：0÷1=0，1÷1=1 。

计算两个二进制数1010和0011的商

 

 

有符号二进制数的算术运算

有符号的二进制数表示:二进制数的最高位表示符号位，且用0表示正数，用1表示负数。其余部分用原码的形式表示数值位。

二进制补码的减法运算：减法运算的原理:减去一个正数相当于加上一个负数A-B=A+(-B)，对(-B)求补码，然后进行加法运算。

如：试用4位二进制补码计算5-2。

（注意符号）

溢出的判断

注意溢出与进位及补码运算中的进位丢失间的区别：

   (1) 进位和借位是指无符号数运算结果的最高位向更高位进位或借位，通常多位二进制数将其拆成二部分或三部分或更多部分进行运算时，数的低位部分均为无符号数，只有最高部分数才为符号数。由此可知：进位主要用于无符号数的运算，这与溢出主要用于符号数的运算是有区别的。

   (2)溢出与补码运算中的进位丢失也应加以区别。

例，两负数相加;-50-5=-55

 

       两负数相加，结果为负数正确。这里虽然出现了补码运算中的进位，但由于和数并没有超出8位二进制数－128～127的范围，因此无溢出，应将进位位丢失，最高位作为符号位

判别溢出与进位的方法：设符号位向进位位的进位为CY，数值部分向符号位的进位为CS ，则溢出：

 O=1，有溢出； O=0，无溢出；

 

码制

BCD码

二—十进制码 (数值编码)，(BCD码—Binary Code Decimal），用4位二进制数来表示一位十进制数中的0~9十个数码。从4 位二进制数16种代码中，选择10种来表示0~9个数码的方案有很多种。每种方案产生一种BCD码。

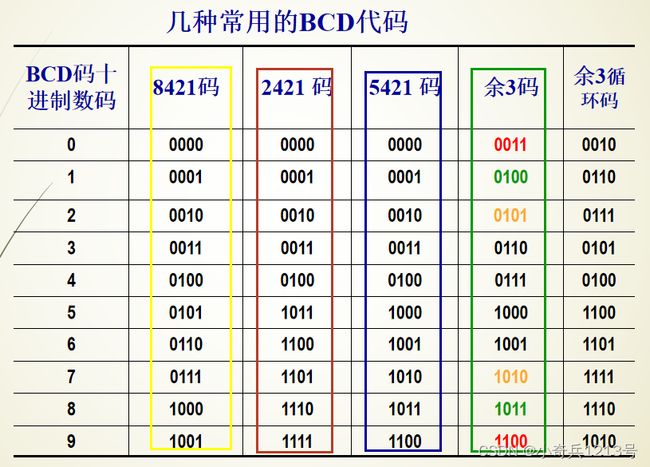
8421码、2421码、5421码都是有权码，其对应的权值对应名称，如8421码表示90即为1001 0000（1001对应=8*1+4*0+2*0+1*0=9，0000对应0）；2421码表示90即为1111 0000（1111对应2*1+4*1+2*1+1*1=9，0000对应0），同理5421码表示90即为1100 0000（1100对应5*1+4*1+2*1+1*1=9，0000对应0）；

用BCD码来表示十进制数：

 

余3码

余3码是由8421BCD码加上0011形成的一种无权码，由于它的每个字符编码比相应的8421码多3，故称为余三码。BCD码的一种。余3码的特点：当两个十进制数的和是9时，相应的余3码的和正好是15，于是可自动产生进位信号,而不需修正。1(0100)和9(1100), 2(0101)和8(1011),…6(1001)和4(0111)的余３码互为反码,这在求对于模9的补码很方便。

余3循环码

每一位的1并不代表固定的数值，它具有格雷码的优点，相邻的两个代码之间仅一位的状态不同。按余3码循环码组成计数器时，每次转换过程只有一个触发器翻转，译码时不会发生竞争－冒险现象。（变权码）

格雷码

格雷码是一种常见的无权码，特点是任何两个相邻代码之间仅有一位取值不同。其首、尾两个代码之间也只有一位不同，因此，格雷码又称为循环码。

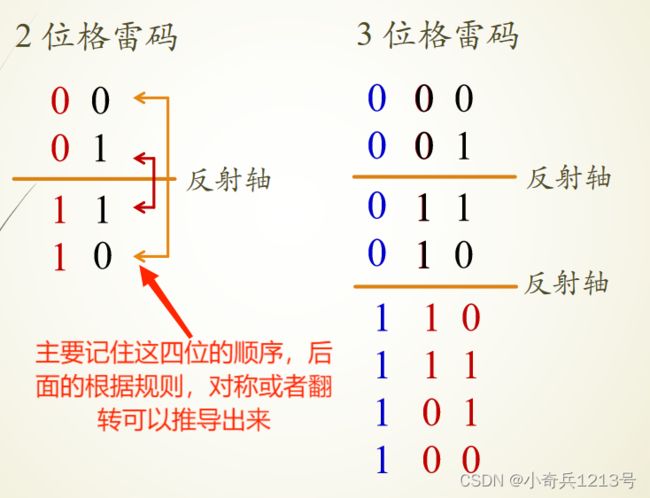
此外，格雷码最高位的0和1只改变一次；若以最高位的0和1之间的交界为轴，其他位的代码是上下对称的。所以，格雷码又是反射码。

格雷码是一种错误最小化的编码。当模拟量发生微小变化，格雷码仅仅改变一位，这与其它码同时改变2位或更多的情况相比，更加可靠,且容易检错。例如，传输十进制的3到4，二进制是011到100三位都发生变化，但格雷码是010到110，只有b2发生变化。

格雷码构成方法：

一位格雷码有两个代码：0 和 1。

(n+1)位格雷码中的前 2^n个代码是将 n位格雷码，按顺序排列，最高位补0。

(n+1)位格雷码中的后 2^n个代码是将n位格雷码，按倒序排列，最高位补1

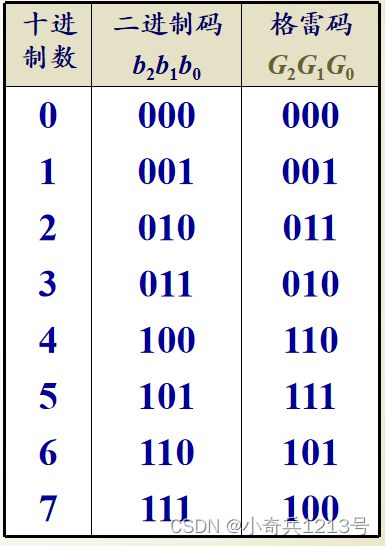
 3位二进制码与格雷码

4位二进制与格雷码： 

 

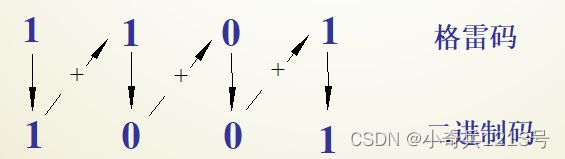
二进制码到格雷码的转换

（1）格雷码的最高位（最左边）与二进制码的最高位相同。

（2）从左到右，逐一将二进制码相邻的两位相加（舍去进位），作为格雷码的下一位。

 

格雷码到二进制码的转换

（1）二进制码的最高位（最左边）与格雷码的最高位相同。

（2）将产生的每一位二进制码，与下一位相邻的格雷码相加（舍去进位），作为二进制码的下一位。

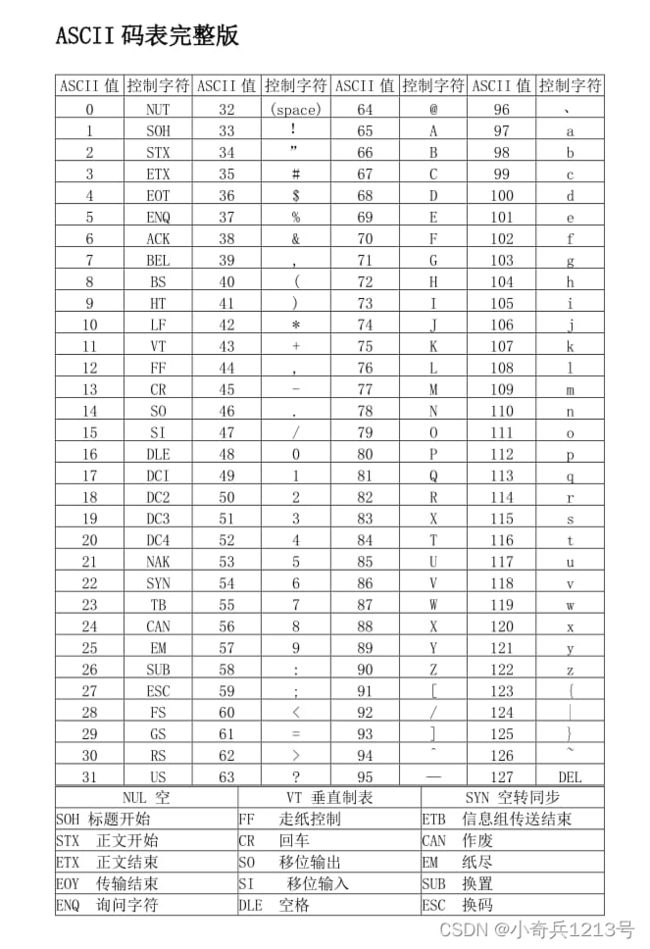
 ASCII码

ASCII码即美国标准信息交换码，是一种字符编码标准，它共有128个代码，可以表示大、小写英文字母、十进制数、标点符号、运算符号、控制符号等，每个字符都用一个7位的二进制数表示，可以表示的字符范围是0-127。普遍用于计算机的键盘指令输入和数据等。

Unicode码

unicode码是一种国际标准编码，它用于表示字符和文本，是一种计算机科学中的标准，用于表示文本和字符。它可以表示世界上所有语言的字符，包括汉字、字母和其他符号，是一种多字节编码系统，可以表示世界上大多数语言的字符，它是一种用于表示文本的编码系统，可以用来表示几乎所有的字符。

Unicode的全称是“统一码”，它是一种字符编码系统，用于表示字符和文本，它使用多字节编码，可以表示世界上大多数语言的字符，它的目的是使用一种编码系统来表示世界上所有语言的字符，以便它们可以在计算机系统中进行交换和处理。

对该编码的进一步认识可在该文章中学习：

https://blog.csdn.net/LemonWatermelon/article/details/90300413

UTF-8编码

UTF-8编码是针对Unicode的一种可变长度字符编码。它可以用来表示Unicode标准中的任何字符，而且其编码中的第一个字节仍与ASCII相容，使得原来处理ASCII字符的软件无须或只进行少部分修改后，便可继续使用。因此，它逐渐成为电子邮件、网页及其他存储或传送文字的应用中，优先采用的编码。

ASCII码、Unicode码、UTF-8编码是目前键盘输入信息的输入法原理。ASCII编码是1个字节，而Unicode编码通常是2个字节。ASCII是单字节编码，无法用来表示中文；而Unicode可以表示所有语言。用Unicode编码比ASCII编码需要多一倍的存储空间。UTF-8编码是基于Unicode编码优化为“可变长编码”，可节省空间提高效率。