MATLAB图论合集（一）基本操作基础

本帖总结一些经典的图论问题，通过MATLAB如何计算答案。近期在复习考研，以此来巩固一下相关知识——虽然考研肯定不能用MATLAB代码哈哈，不过在实际应用中解决问题还是很不错的，比C++易上手得多~

---

        图论中的图（Graph）是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事 物间具有这种系。

        一个图可以用数学语言描述为G(V(G),E(G)) 。

        V(vertex)指 的是图的顶点集，E(edge)指的是图的边集。

1.有向图：弧是顶点的有序对，通过grapi（s,t）函数绘制。s和t分别是两个边两端的点集

   无向图：边是顶点的无序对，通过digrapi（s,t)函数绘制。

% 函数graph(s,t)：可在 s 和 t 中的对应节点之间创建边，并生成一个图
s=[1 1 2 2 2 4 4 3 3 5];
t=[2 3 3 4 5 3 5 5 6 6];
%s和t为端点的集合
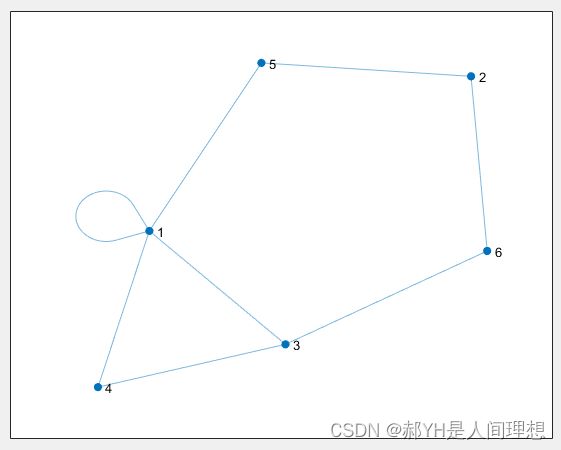
G1=graph(s,t);
plot(G1)
%绘制无向图
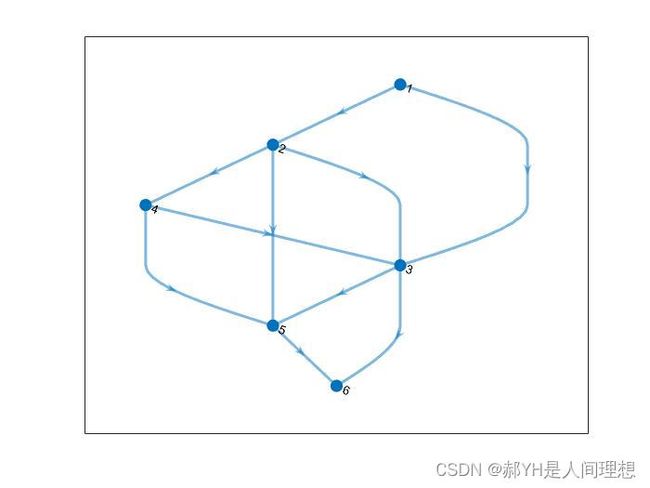
G2=digraph(s,t);
%绘制有向图
plot(G2)

 2.领接矩阵

无向图的领接矩阵必须是对称的，意义为两端点间相互建立联系；而有向图则仅需要从头到尾处建立连接即可（列向为起点，行向为终点）

 

如上图，对于一个相同的邻接矩阵，画出的有向图与无向图形状差距在于边数——对于对称的邻接矩阵，其画为有向图后两节点之间必定各有两条边。 

A1=[1,0,1,1,1,0;
    0,0,0,0,1,1;
    1,0,0,1,0,1;
    1,0,1,0,0,0;
    1,1,0,0,0,0;
    0,1,1,0,0,0;
    ];
G1=graph(A1);
%plot(G1)
G2=digraph(A1);
plot(G2)

3.增加与删除

• addedge：添加新边
• rmedge：删除边
• addnode：添加节点
• rmnode：删除指定节点
• numegdes：边的数量
• numnodes：节点的数量

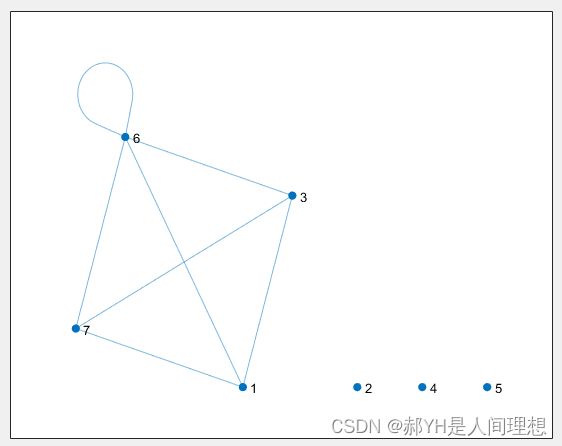
此处演示一下增加节点的效果：

s3=[7,7,7,3,3,1,6];
t3=[3,1,6,1,6,6,6];
G3=graph(s3,t3);
G3=G3.addnode(3);
G3=G3.addedge(2,4);

plot(G3)

 

4.添加权重and命名结点

s=[1 1  2 3 3  5 6 7 5 2];
t=[2 4  7 4 6  8 7 8 6 8];
weights=[13 19 25 17 11 10  92 29 9 3 ];
names={'H' 'Y' '+' '&' 'J' 'S' 'L' '32'};
G=graph(s,t,weights,names);
plot(G,'EdgeLabel',weights)

（至于一些修改图片样式的操作，本贴暂不更新，后期抽空会出绘图专题~）