剑指offer:JZ61 序列化二叉树
描述
请实现两个函数,分别用来序列化和反序列化二叉树,不对序列化之后的字符串进行约束,但要求能够根据序列化之后的字符串重新构造出一棵与原二叉树相同的树。
二叉树的序列化是指:把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串,从而使得内存中建立起来的二叉树可以持久保存。序列化可以基于先序、中序、后序、层序的二叉树等遍历方式来进行修改,序列化的结果是一个字符串,序列化时通过 某种符号表示空节点(#),以 ! 表示一个结点值的结束(value!)。
二叉树的反序列化是指:根据某种遍历顺序得到的序列化字符串结果str,重构二叉树。
例如,可以根据层序遍历并特定标志空结点的方案序列化,也可以根据满二叉树结点位置的标号规律来序列化,还可以根据先序遍历和中序遍历的结果来序列化。
假如一棵树共有 2 个结点, 其根结点为 1 ,根结点右子结点为 2 ,没有其他结点。按照上面第一种说法可以序列化为“1,#,2,#,#”,按照上面第二种说法可以序列化为“{0:1,2:2}”,按照上面第三种说法可以序列化为“1,2;2,1”,这三种序列化的结果都包含足以构建一棵与原二叉树完全相同的二叉树的信息。
不对序列化之后的字符串进行约束,所以欢迎各种奇思妙想。
/* TreeNode类的代码
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
示例
input:
{8,6,10,5,7,9,11}
output:
{8,6,10,5,7,9,11}
思路
根据题目的要求,需要将二叉树序列化为字符串并且能够还原即可,本题中的要点是对树进行还原。根据题干的要求,主要有3种方法序列化为字符串:队列的层次遍历、递归的先序或后序遍历、先序+中序遍历。
1、队列遍历:层次遍历
二叉树的层次遍历的思路是:由根节点开始,从上往下一层层的遍历;在每一层中,按照从左到右的顺序遍历。根据这种遍历的特点,一般使用队列。
(1)队列实现二叉树的层次遍历
队列的特性是先进先出,因此使用队列来层次遍历时,需要:
- 先加入根节点,确保队列不为空
- 队列不为空时,取出队列的元素,依次加入该结点的左右子树
- 重复上一步,直到队列为空
由于队列遍历二叉树时,每次循环字符串中依次加入左右两个子树的结点(为空则用#替代),因此最后的字符串中,每一个根结点必然有左右子结点(叶子结点的左右结点依次为#、#)。基于这个特性,根据字符串重构二叉树时,可以使用队列来反序列化:
- 将序列化的字符串按照
,切割为字符串数组,数组中每个字符串表示一个结点;队列中首先加入根结点 - 由于序列化时每次加入左右子树,因此反序列化时,也要依次解出左右子树(遇到
#时,直接进入下一个字符串);与此同时,不为空的结点需要加入到队列中 - 重复上一步,直到队列为空或者数组索引越限
可以看到的是,队列在整个序列化和反序列化中,可以筛选叶子结点
- 在序列化中,队列只会加入不为空的结点,防止
null加入 - 在反序列化中,队列通过阻断叶子结点
#,从而让字符串中的索引刚好对上队列poll结点的左右子树
import java.util.*;
public class Solution {
String Serialize(TreeNode root) {
if(root == null) return null;
Queue<TreeNode> que = new LinkedList<>();
//队列先加入根结点,字符串加入根结点的值,以','分割
que.offer(root);
StringBuilder sb = new StringBuilder(root.val + ",");
TreeNode tmp = null;
while(!que.isEmpty()){
//取出当前结点之后,字符串中依次加入左右子树的结点
tmp = que.poll();
if(tmp.left != null){
sb.append(tmp.left.val + ",");
que.offer(tmp.left);
}else sb.append("#,");
if(tmp.right != null){
sb.append(tmp.right.val + ",");
que.offer(tmp.right);
}else sb.append("#,");
}
return sb.toString();
}
TreeNode Deserialize(String str) {
if(str == null) return null;
String[] e = str.split(",");
Queue<TreeNode> que = new LinkedList<>();
TreeNode root = new TreeNode(Integer.parseInt(e[0]));
TreeNode tmp = null;
que.offer(root);//加入根结点
int idx = 1;
while(!que.isEmpty() && idx < e.length){
tmp = que.poll();
if(e[idx].charAt(0) != '#'){
tmp.left = new TreeNode(Integer.parseInt(e[idx]));
que.offer(tmp.left);
}
idx++;
if(idx < e.length && e[idx].charAt(0) != '#'){
tmp.right = new TreeNode(Integer.parseInt(e[idx]));
que.offer(tmp.right);
}
idx++;
}
return root;
}
}

注意:由于Queue不能加入null元素,因此队列的while循环不能这样写:
que.offer(root);
StringBuilder sb = new StringBuilder();
TreeNode tmp = null;
while(!que.isEmpty()){
tmp = que.poll();
sb.append(tmp == null ? "#," : tmp.val + ",");
que.offer(tmp.left);
que.offer(tmp.right);
}
2、递归版遍历:先序、后序
由于本题中要求根据序列化的结果来反序列化出二叉树,因此,在序列化的结果中,叶子结点可以使用#代替,因此每一个结点都含有左右子树(没有子树的用#代替,如下图中2的右子树为空,但序列化中用#表示其右子树)。这么做的好处是:在反序列化时,确保每一个结点都有左右子树(字符为#表示子树为null,否则表示有真实的子树),这样的写法非常适合递归来实现。
在先序和后续遍历中,根结点的位置可以直接确定,因此这两种遍历中任何一个都可以直接反序列化出二叉树;而中序遍历的序列化结果中,由于无法确定二叉树根结点的位置,因此只依靠中序遍历无法反序列化出二叉树。在后面将会用结合中序和先序、中序和后续来反序列化二叉树。
(1)递归先序遍历
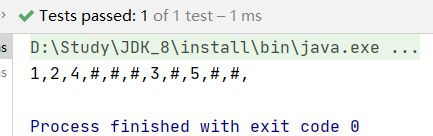
二叉树的先序遍历的思路是:先访问根结点,然后先序遍历左子树,最后先序遍历右子树。在使用递归实现时,需要先访问根结点,如果还有左子树,那么需要访问左子树的根结点… …如此递归直到最左边的叶子结点(如下图中的结点4),此时该叶子结点对应的父结点如果有右子树,则先序访问右子树。下图中的先序遍历的顺序为:1-2-4-3-5,下面代码中序列化的字符串结果为:1,2,4,#,#,#,3,#,5,#,#,
public class Solution {
//推荐下面更简洁的写法
StringBuilder pre_dfs(TreeNode node, StringBuilder sb){
sb.append(node.val + ",");
if(node.left != null) pre_dfs(node.left, sb);
else sb.append("#,");
if(node.right != null) pre_dfs(node.right, sb);
else sb.append("#,");
return sb;
}
String Serialize(TreeNode root) {
return root == null? null : pre_dfs(root,new StringBuilder()).toString();
}
int i = 0;
TreeNode de_pre(String[] str){
if(str[i].charAt(0) == '#'){
i++;
return null;
}
TreeNode node = new TreeNode(Integer.parseInt(str[i]));
i++;//寻找下一个结点
node.left = de_pre(str);
node.right = de_pre(str);
return node;
}
TreeNode Deserialize(String str) {
if(str == null) return null;
return de_pre(str.split(","));
}
}
@Test
public void Serialize_Binarytree_pre(){
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.right.right = new TreeNode(5);
System.out.println(Serialize(root));
}
由于是递归,因此代码中的序列化过程可以有许多写法,比如下面的写法可以更简洁:
//序列化写法2:直接使用字符串拼接,由于java底层做了优化,因此速度也非常快
String Serialize(TreeNode root) {
if(root == null) return "#,";
return root.val + "," + Serialize(root.left) + Serialize(root.right);
}
同样,反序列化也可以直接使用charAt函数来对字符串逐字符读取或者将字符串切为数组存为List作为参数
//反序列化写法2:不用split,直接使用字符串的索引来读取
int i = 0;
TreeNode Deserialize(String str) {
TreeNode node = null;
if(str == null || i >= str.length() - 1) return node;
int j = i;
if(str.charAt(i) == '#'){
i = i + 2;
return node;
}
else{
while(str.charAt(i) != ',') i++;
node = new TreeNode(Integer.parseInt(str.substring(j,i)));
i++;
node.left = Deserialize(str);
node.right = Deserialize(str);
}
return node;
}
//反序列化写法3:不用索引,直接使用ArrayList
TreeNode de_help(ArrayList<String> arr){
if(arr.get(0).charAt(0) == '#'){
arr.remove(0);
return null;
}
TreeNode node = new TreeNode(Integer.parseInt(arr.get(0)));
arr.remove(0);
node.left = de_help(arr);
node.right = de_help(arr);
return node;
}
TreeNode Deserialize(String str) {
if(str.charAt(0) == '#') return null;
ArrayList<String> arr = new ArrayList<>(Arrays.asList(str.split(",")));
return de_help(arr);
}
(2)递归后序遍历
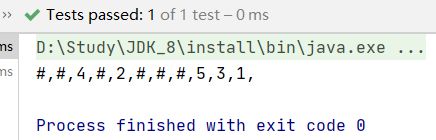
二叉树的后序遍历的思路是:先后序遍历左子树,然后后序遍历右子树,最后访问根结点。实现的方法和先序类似,在递归时需要从字符串数组的最后一个元素开始往前面读。下图中的先序遍历的顺序为:4-2-5-3-1,下面代码中序列化的字符串结果为:#,#,4,#,2,#,#,#,5,3,1,
import java.util.ArrayList;
import java.util.Arrays;
public class Solution {
String Serialize(TreeNode root) {
if(root == null) return "#,";
return Serialize(root.left) + Serialize(root.right) + root.val + "," ;
}
TreeNode post_help(ArrayList<String> arr){
int tail_idx = arr.size() - 1;
if(arr.get(tail_idx).charAt(0) == '#'){
arr.remove(tail_idx);
return null;
}
TreeNode node = new TreeNode(Integer.parseInt(arr.get(tail_idx)));
arr.remove(tail_idx);
node.right = post_help(arr);
node.left = post_help(arr);
return node;
}
TreeNode Deserialize(String str) {
if(str.length() == 2) return null;
ArrayList<String> arr = new ArrayList<>(Arrays.asList(str.split(",")));
return post_help(arr);
}
}
@Test
public void Serialize_Binarytree_post(){
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.right.right = new TreeNode(5);
System.out.println(Serialize(root));
}
3、不使用#填充:先序+中序、中序+后续
在普通的二叉树遍历中,通常可以使用题目中两个遍历的结果来重构二叉树,但是该方法的前提是,二叉树中各个结点的值不相同。
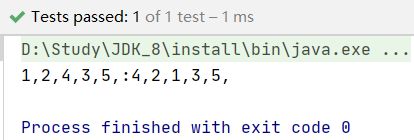
如图二叉树,先序遍历结果为:1,2,4,3,5;中序遍历的结果为:4,2,1,3,5;后序遍历的结果为:4,2,5,3,1
三种遍历的代码如下:
//StringBuilder作为参数的先序结果:sb.toString() = "1,2,4,3,5,"
void pre_order_sb(TreeNode root, StringBuilder sb){
if(root == null) return;
sb.append(root.val+",");
pre_order_sb(root.left, sb);
pre_order_sb(root.right,sb);
}
//栈实现的先序结果:"1,2,4,3,5,"
String pre_order(TreeNode root){
if(root == null) return null;
StringBuilder sb = new StringBuilder();
Stack<TreeNode> st = new Stack<>();
st.push(root);
TreeNode tmp = null;
//先序遍历:根、左子树、右子树
while(!st.isEmpty()) {
tmp = st.pop();
sb.append(tmp.val + ",");
//注意:这里需要先加右子树,才能保证左子树先出栈
if(tmp.right != null) st.push(tmp.right);
if(tmp.left != null) st.push(tmp.left);
}
return sb.toString();
}
//递归实现的中序结果:",4,2,1,3,5,"
String in_order_rec(TreeNode root){
return root == null? "," : in_order_rec(root.left) + root.val + in_order_rec(root.right);
}
//栈实现的中序结果:"4,2,1,3,5,"
String in_order(TreeNode root){
if(root == null) return null;
StringBuilder sb = new StringBuilder();
Stack<TreeNode> st = new Stack<>();
st.push(root);
TreeNode tmp = null;
//中序遍历:左子树、根、右子树
while(!st.isEmpty()){
while(st.peek().left != null) st.push(st.peek().left);
while(!st.isEmpty()){
tmp = st.pop();//当前结点无左子树
sb.append(tmp.val + ",");
if(tmp.right != null){
st.push(tmp.right);
break;
}
}
}
return sb.toString();
}
//栈实现的后序结果:"4,2,5,3,1,"
String post_order(TreeNode root){
if(root == null) return null;
StringBuilder sb = new StringBuilder();
Stack<TreeNode> st = new Stack<>();
st.push(root);
TreeNode tmp = null, pre_visit = null;
//后序遍历:左子树、右子树、根
while(!st.isEmpty()){
while(st.peek().left != null) st.push(st.peek().left);
while(!st.isEmpty()){
tmp = st.peek();
if(tmp.right == null || tmp.right == pre_visit){
tmp = st.pop(); //叶子结点或者其右子树已被访问的结点
sb.append(tmp.val+ ",");
pre_visit = tmp;//标记上一次出栈的结点
}
else{
//当前结点还有右子树,则将右子树作为完整的树加入到栈中
st.push(st.peek().right);
break;
}
}
}
return sb.toString();
}
(1)先序+中序
先序遍历的思路是:先遍历根,再遍历左子树,最后遍历右子树,因此先序的序列化结果中,字符串的顺序一定是:根结点、左子树的结点集合、右子树的结点集合。
中序遍历的思路是:先遍历左子树,再遍历根,最后遍历右子树,因此中序的序列化结果中,字符串的顺序一定是:左子树的结点集合、根结点、右子树的结点集合。
根据上面的分析,可知:
- 先序字符串数组中最左边的元素一定是根结点:
TreeNode root = new TreeNode(Integer.parseInt(pre[pl])) - 根据根结点的值在中序字符串数组中找到根结点:
while(!pre[pl].equals(in[idx])) idx++; - 中序数组
in中,根结点索引idx左侧的数组[il, idx-1]一定是左子树的结点集合。根据左子树结点的个数来判断先序数组pre中左子树集合对应的数组索引范围[pl+1, pl+idx-il] - 先序中已经判断出根结点、左子树集合的索引范围,因此剩下的数组范围
[pl+idx-il+1, pr]就是先序的右子树结点集合
下面采用栈遍历的结果反序列化出二叉树:
String Serialize(TreeNode root) {
if(root == null) return null;
return pre_order(root) + ":" + in_order(root);
}
T
reeNode build(String[] pre, int pl, int pr, String[] in, int il, int ir){
if(pl > pr) return null;
int idx = il;
TreeNode root = new TreeNode(Integer.parseInt(pre[pl]));
//在中序中查找根结点的索引
while(!pre[pl].equals(in[idx])) idx++;
root.left = build(pre, pl+1, pl+idx-il, in, il, idx-1);
root.right = build(pre, pl+idx-il+1, pr, in, idx+1, ir);
return root;
}
TreeNode Deserialize(String str) {
if(str == null) return null;
String[] order = str.split(":");
String[] pre = order[0].split(",");
String[] in = order[1].split(",");
return build(pre, 0, pre.length-1, in, 0, in.length-1);
}

使用IntelliJ IDEA查看先序+中序遍历序列化的测试结果:
@Test
public void Serialize_Binarytree_post(){
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.right.right = new TreeNode(5);
System.out.println(Serialize(root));
}