用对角线去遍历矩阵

声明

该系列文章仅仅展示个人的解题思路和分析过程，并非一定是优质题解，重要的是通过分析和解决问题能让我们逐渐熟练和成长，从新手到大佬离不开一个磨练的过程，加油！

原题链接

用对角线遍历矩阵https://leetcode.cn/leetbook/read/array-and-string/cuxq3/

算法分析

图一

图二

图三

图四

       

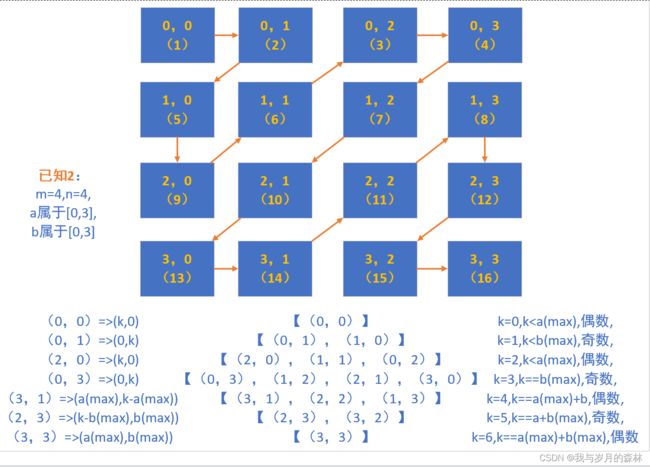
由上述四个图可以总结得出以下八个结论： 

结论1：k属于[0,a(max)+b(max)]。

结论2：每一层遍历行最多存在min(m,n)个矩阵索引对，min(m,n)表示m和n二者中小的那一个值。

结论3：a属于[0,m-1]，b属于[0,n-1]。

结论4：若k为偶数则以a为比较对象，此时若k<=a(max)则当前遍历行的起始索引对为(k,0)，反之则起始索引对为(a(max),k-a(max))。

结论5：若k为奇数则以b为比较对象，此时若k<=b(max)则当前遍历行的起始索引对位(0,k)，反之则起始索引对为(k-b(max),b(max))。

结论6：从当前遍历行的起始索引对开始，若k为偶数，则下一个索引对为(a-1,b+1)，反之下一个索引对为(a+1,b-1)。

结论7：遍历行的结束条件由该矩阵的遍历行最大索引对个数和a(min)、b(min)共同决定，首先应判断当前遍历行访问的矩阵索引对个数是否达到了该矩阵的遍历行最大索引对个数，若达到了则完成该遍历行的遍历，否则判断下一个索引对(a,b)，若a或b越界则表明完成该遍历行的遍历。

结论8：整个矩阵遍历结束的条件是当前遍历的矩阵索引对的个数是m×n个。

 代码示例（C#）

public int[] FindDiagonalOrder(int[][] mat)
{
    int m = mat.Length;//矩阵的行数
    int n = mat[0].Length;//矩阵的列数
    int[] result = new int[m * n];//结果数组
    //a:索引对的a,b:索引对的b,k:a+b,count:当前已遍历的矩阵索引对个数,minA:a的最小值
    //minB:b的最小值,index:结果数组中的索引指针
    int a, b, k = 0, count = 0, minA = 0, minB = 0, index = 0;
    int maxA = m - 1;//a的最大值
    int maxB = n - 1;//b的最大值
    int maxIndexsCount = m <= n ? m : n;//该矩阵中遍历行的矩阵索引对个数的最大值
    int lineIndexsCount;//遍历行当前已遍历的矩阵索引对个数
    while (count < m * n)
    {
        lineIndexsCount = 0;
        //若k%2为0则表示k为偶数，反之则为奇数
        if (k % 2 == 0)
        {
            if (k <= maxA)
            {
                a = k;
                b = 0;
            }
            else
            {
                a = maxA;
                b = k - maxA;
            }
        }
        else
        {
            if (k <= maxB)
            {
                a = 0;
                b = k;
            }
            else
            {
                a = k - maxB;
                b = maxB;
            }
        }
        while (lineIndexsCount < maxIndexsCount)
        {
            //a或b越界则完成此次遍历行的遍历
            if ((a < minA || a > maxA) || (b < minB || b > maxB)) break;
            //记录结果
            result[index++] = mat[a][b];
            count++;
            if (k % 2 == 0)
            {
                a--;
                b++;
            }
            else
            {
                a++;
                b--;
            }
        }
        k++;
    }
    return result;
}

算法解说 

        按照原题的思路我们列举出了四种矩阵，严格来说只有三种，分别是矩阵行数大于列数、行数等于列数、行数小于列数，而为了保证后续结论的真实性，我们列举了两个行数等于列数的矩阵。

        图中我们完成了四个矩阵的制定，然后按照题目要求去遍历了四个矩阵并且将遍历的结果记录下来，从行列定义上我们可以将矩阵构建在二维平面中，从而为每一个元素设立一个唯一的坐标值，在本题中我们把这个坐标值称为索引对。有了索引对我们可以进一步按照索引对两个数值之和对遍历结果进行分组，在本题中我们把索引对两个数值之和相同的一组索引对称为遍历行，为了简便后续将索引对两个数值之和称为索引对结果值。

        将遍历行按照索引对结果值从小到大的顺序进行排列，为了能够发现更多有用的结论，我们把每一层遍历行的索引对结果值、结果值的奇偶性、索引对与k值的关系列举出来，除此之外还需要列举出矩阵行列数以及索引对两个数值的取值范围，至于为什么要去列举这些东西，实际上还是通过尝试和思考，就像上学时做数学题，浏览题目之后列举出题目中给定的条件，然后根据条件去解题。

        这一步我们可以理解为进一步细化和剖析已知条件，我们的目的是从已知条件中获取可靠的结论，从而根据结论解决问题，因此我们总结出了上文的八个结论。

        那么已知结论后如何去编写代码呢？本人是按照以下几个问题去解决的。

        1.我们需要明白输入和输出是什么？

        2.我们需要定义哪些变量？

        3.函数主体是什么？

        4.某些过程的结束条件是什么？

        实际上，就是将我们的八个结论构建为代码，简单划分就是定义变量和逻辑主体，定义变量就看结论中需要记录数据的描述，逻辑主体就看结论中对于逻辑处理、结束条件的描述。

        当然这样转换出来的代码比较粗糙，所以后续还可以结合自己的编程知识再去优化自己的代码，让它变得更加简洁精致。