差值结构不对称部分的约化质心

( A, B )---5*30*2---( 1, 0 )( 0, 1 )

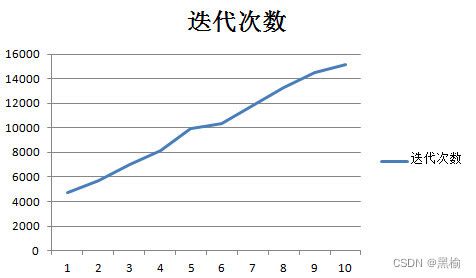
做一个网络，输入为5个点，训练集A,B各有两张图片。让B的两张图片全是0.排列组合A，记录迭代次数平均值的变化。

迭代了1024组，共收集到33组不同的数据，其中对称的部分有17组，不对称的有15组.31*31-0*0是分界线。

	4*30*2	5*30*2
	256	1024
	21	33
不对称	8	15
对称	12	17

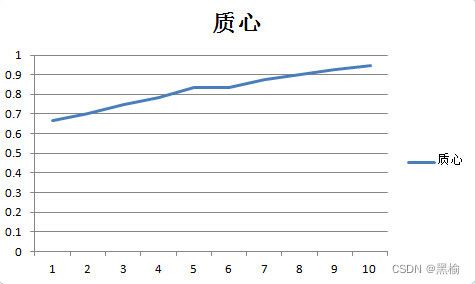
这次继续用计算质心的办法去拟合迭代次数，

	0	1	2	3	4
	0	1	0	1	0	10*22-0*0
	1	0	1	1	0	10*22-0*0
		坐标				质量				坐标*质量
0		0	0	0		1	1	1		0	0	0
1		1.5	0	1.5		1	1	1		1.5	0	1.5
2		0	0	0		1	1	1		0	0	0
3		3.5	0	1.5		1	1	1		3.5	0	1.5
4		0	0	0		1	1	1		0	0	0
0		0.5	0	0.5		1	1	1		0.5	0	0.5
1		0	0	0		1	1	1		0	0	0
2		2.5	0	0.5		1	1	1		2.5	0	0.5
3		3.5	0	0.5		1	1	1		3.5	0	0.5
4		0	0	0		1	1	1		0	0	0
										12	0	4.5
										质心坐标
								5		2.3	0	0.9

两行x的坐标都是0.5，1.5，2.5，3.5，4.5，y坐标为0，z坐标第一行是0.5，第二行是1.5.则10*22-0*0的质心为(2.3,0,0.9).

得到数据为

差值结构					网络	迭代次数						质心x	y	z
0	0	0	1	0	2*31-0*0	4766.377		6	1	5		2.16667	0	0.66667
1	1	1	1	1	2*31-0*0	4766.377		6	1	5
								6	1	5
0	1	0	0	0	8*30-0*0	5682.156		5	1	4		1.7	0	0.7
1	1	1	1	0	8*30-0*0	5682.156		5	1	4
								5	1	4
0	0	0	1	0	2*14-0*0	7016.286		4	1	3		1.25	0	0.75
0	1	1	1	0	2*14-0*0	7016.286		4	1	3
								4	1	3
0	1	0	1	0	10*31-0*0	8185.151		7	2	5		2.5	0	0.78571
1	1	1	1	1	10*31-0*0	8185.151		7	2	5
								7	2	5
0	1	0	1	0	10*30-0*0	9968.608		6	2	4		2.16667	0	0.83333
1	1	1	1	0	10*30-0*0	9968.608		6	2	4
								6	2	4
0	0	1	0	0	4*12-0*0	10341.13		3	1	2		2.16667	0	0.83333
0	1	1	0	0	4*12-0*0	10341.13		3	1	2
								3	1	2
1	0	1	0	1	21*31-0*0	11793.89		8	3	5		2.5	0	0.875
1	1	1	1	1	21*31-0*0	11793.89		8	3	5
								8	3	5
0	0	1	0	1	5*7-0*0	13311.64		5	2	3		3.5	0	0.9
0	0	1	1	1	5*7-0*0	13311.64		5	2	3
								5	2	3
0	1	0	0	1	9*23-0*0	14500.69		6	2	4		2.83333	0	0.83333
1	0	1	1	1	9*23-0*0	14500.69		6	2	4
								6	2	4
0	1	0	0	0	8*23-0*0	14608.61		5	1	4		2.5	0	0.7
1	0	1	1	1	8*23-0*0	14608.61		5	1	4
								5	1	4
1	0	0	1	1	19*27-0*0	14486.38		7	3	4		2.64286	0	0.92857
1	1	0	1	1	19*27-0*0	14486.38		7	3	4
								7	3	4
1	1	0	1	1	27*31-0*0	15154.8		9	4	5		2.5	0	0.94444
1	1	1	1	1	27*31-0*0	15154.8		9	4	5
								9	4	5
0	1	0	1	1	11*23-0*0	16791.92		7	3	4		2.92857	0	0.92857
1	0	1	1	1	11*23-0*0	16791.92		7	3	4
								7	3	4
0	1	0	0	0	8*22-0*0	17517.73		4	1	3		3	0	0.75
1	0	1	1	0	8*22-0*0	17517.73		4	1	3
								4	1	3
0	1	0	1	0	10*22-0*0	17793.41		5	2	3		2.1	0	0.9
1	0	1	1	0	10*22-0*0	17793.41		5	2	3
								5	2	3
1	1	1	1	1	31*31-0*0	18794.76		#	5	5
1	1	1	1	1	31*31-0*0	18794.76		#	5	5		1024
								#	5	5
1	0	1	1	1	23*23-0*0	19454.11		8	4	4
1	0	1	1	1	23*23-0*0	19454.11		8	4	4
								8	4	4
0	1	1	1	1	15*30-0*0	19855.73		8	4	4
1	1	1	1	0	15*30-0*0	19855.73		8	4	4
								8	4	4
1	1	1	0	0	28*28-0*0	20593.18		6	3	3
1	1	1	0	0	28*28-0*0	20593.18		6	3	3
								6	3	3
0	1	0	1	1	11*26-0*0	21390.39		6	3	3
1	1	0	1	0	11*26-0*0	21390.39		6	3	3
								6	3	3
1	0	1	0	1	21*10-0*0	21925.96		5	3	2
0	1	0	1	0	21*10-0*0	21925.96		5	3	2
								5	3	2
0	1	0	0	0	8*20-0*0	22413.93		3	1	2
1	0	1	0	0	8*20-0*0	22413.93		3	1	2
								3	1	2
0	0	1	1	1	7*28-0*0	22662.79		6	3	3
1	1	1	0	0	7*28-0*0	22662.79		6	3	3
								6	3	3
0	1	1	0	0	12*12-0*0	22636.98		4	2	2
0	1	1	0	0	12*12-0*0	22636.98		4	2	2
								4	2	2
0	0	1	0	1	5*20-0*0	24238.5		4	2	2
1	0	1	0	0	5*20-0*0	24238.5		4	2	2
								4	2	2
0	0	0	0	0	0*31-0*0	25756.47		5	0	5
1	1	1	1	1	0*31-0*0	25756.47		5	0	5
								5	0	5
0	0	0	0	0	0*30-0*0	27150.64		4	0	4
1	1	1	1	0	0*30-0*0	27150.64		4	0	4
								4	0	4
1	0	0	0	0	16*16-0*0	27122.25		2	1	1
1	0	0	0	0	16*16-0*0	27122.25		2	1	1
								2	1	1
0	1	0	1	0	10*5-0*0	27287.88		4	2	2
0	0	1	0	1	10*5-0*0	27287.88		4	2	2
								4	2	2
0	0	0	0	0	0*28-0*0	29376.11		3	0	3
1	1	1	0	0	0*28-0*0	29376.11		3	0	3
								3	0	3
0	0	0	0	0	0*24-0*0	32971.82		2	0	2
1	1	0	0	0	0*24-0*0	32971.82		2	0	2
								2	0	2
0	0	0	0	1	1*2-0*0	33618.72		2	1	1
0	0	0	1	0	1*2-0*0	33618.72		2	1	1
								2	1	1
0	0	0	0	0	0*4-0*0	40885.45		1	0	1
0	0	1	0	0	0*4-0*0	40885.45		1	0	1
								1	0	1

不对称部分的15组可以拟合其中的10组。

网络	迭代次数	质心z
2*31-0*0	4766.377	0.666667
8*30-0*0	5682.156	0.7
2*14-0*0	7016.286	0.75
10*31-0*0	8185.151	0.785714
10*30-0*0	9968.608	0.833333
4*12-0*0	10341.13	0.833333
21*31-0*0	11793.89	0.875
5*7-0*0	13311.64	0.9
19*27-0*0	14486.38	0.928571
27*31-0*0	15154.8	0.944444

拟合这两组数据

质心=0.0533463084569849*迭代次数**0.2981490239995757

0.9986715201061859   ******  决定系数 r**2

但有5组数据异常

												计算质心	约化z坐标	与1.5的差值
0	1	0	0	1	9*23-0*0	14500.69		2.83	0	0.83		0.928578	2.07	0.57
1	0	1	1	1	9*23-0*0	14500.69
0	1	0	0	0	8*23-0*0	14608.61		2.5	0	0.7		0.930633	2.65	1.15
1	0	1	1	1	8*23-0*0	14608.61
0	1	0	1	1	11*23-0*0	16791.92		2.93	0	0.93		0.970094	1.8	0.3
1	0	1	1	1	11*23-0*0	16791.92
0	1	0	0	0	8*22-0*0	17517.73		3	0	0.75		0.982411	2.42	0.92
1	0	1	1	0	8*22-0*0	17517.73
0	1	0	1	0	10*22-0*0	17793.41		2.1	0	0.9		0.986995	1.93	0.43
1	0	1	1	0	10*22-0*0	17793.41

这5组里都有

0	1	0
1	0	1

2*5这样的对称结构。现在用这5组的迭代次数计算出这5组的质心，然后计算

0	1	0
1	0	1

对称结构第二行1的修正z坐标，用这个约化坐标重新计算10*22-0*0的质心为

		0	1	2	3	4
		0	1	0	1	0	10*22-0*0
		1	0	1	1	0	10*22-0*0
			坐标				质量				坐标*质量
	0		0	0	0		1	1	1		0	0	0
	1		1.5	0	1.93		1	1	1		1.5	0	1.93
	2		0	0	0		1	1	1		0	0	0
	3		3.5	0	1.5		1	1	1		3.5	0	1.5
	4		0	0	0		1	1	1		0	0	0
	0		0.5	0	0.5		1	1	1		0.5	0	0.5
	1		0	0	0		1	1	1		0	0	0
	2		2.5	0	0.5		1	1	1		2.5	0	0.5
	3		3.5	0	0.5		1	1	1		3.5	0	0.5
	4		0	0	0		1	1	1		0	0	0
											12	0	4.93
											质心坐标
									5		2.3	0	0.986

如果第二行只有1个1这个修正约为1，如果有两个1修正约为0.5，如果有3个1修正为0.3.