【Sklearn】基于支持向量机算法的数据分类预测(Excel可直接替换数据)
【Sklearn】基于支持向量机算法的数据分类预测(Excel可直接替换数据)
- 1.模型原理
-
- 1.1 数学模型
- 1.2 模型原理
- 2.模型参数
- 3.文件结构
- 4.Excel数据
- 5.下载地址
- 6.完整代码
- 7.运行结果
1.模型原理
支持向量机(Support Vector Machine,SVM)是一种用于分类和回归的监督学习算法,其基本思想是在特征空间中找到一个能够最大化分类间隔(Margin)的超平面,从而将不同类别的样本正确分类。以下是SVM的数学模型和模型原理的解释:
1.1 数学模型
假设我们有一个训练数据集,包含 N N N个样本,每个样本由特征向量 X i X_i Xi和对应的标签 y i y_i yi组成,其中 X i X_i Xi是一个 n n n维特征向量, y i y_i yi是样本的标签(+1表示正例,-1表示负例)。
SVM的分类目标是找到一个超平面,它可以将不同类别的样本分开,并且使得两个类别的样本都尽可能远离这个超平面。这个超平面可以表示为:
w ⋅ x + b = 0 w \cdot x + b = 0 w⋅x+b=0
其中, w w w是法向量(权重向量)决定了超平面的方向, b b b是偏差(截距), x x x是特征向量。
SVM的基本分类问题可以定义为:
Minimize 1 2 ∣ ∣ w ∣ ∣ 2 Subject to y i ( w ⋅ x i + b ) ≥ 1 for all i = 1 , 2 , … , N \begin{align*} \text{Minimize} \quad & \frac{1}{2} ||w||^2 \\ \text{Subject to} \quad & y_i (w \cdot x_i + b) \geq 1 \quad \text{for all } i = 1, 2, \ldots, N \end{align*} MinimizeSubject to21∣∣w∣∣2yi(w⋅xi+b)≥1for all i=1,2,…,N
这里的目标是最小化 w w w的范数(求解一个最大间隔),约束条件确保每个样本都在正确的一侧,距离超平面足够远。
1.2 模型原理
-
最大间隔: SVM的核心思想是寻找一个能够最大化分类间隔(Margin)的超平面。Margin是指离超平面最近的样本点到超平面的距离之和,SVM试图找到一个超平面,使得Margin最大。
-
支持向量: 在分类问题中,离超平面最近的样本点被称为支持向量(Support Vectors)。它们是决定超平面位置的关键点,而其他样本点对于超平面的位置没有影响。
-
软间隔与松弛变量: 在实际数据中,样本不一定总是线性可分的。为了应对这种情况,SVM引入了松弛变量(Slack Variables),允许一些样本处于Margin内部,甚至错分。这就是软间隔(Soft Margin)的概念。
-
核函数: SVM可以通过核函数将低维特征映射到更高维的特征空间,从而可以处理非线性分类问题。常用的核函数有线性核、多项式核、高斯核等。
-
优化问题: SVM的分类问题可以转化为一个凸优化问题,可以使用凸优化算法(如序列最小优化算法、SMO)求解。
-
对偶问题: SVM的优化问题可以通过拉格朗日对偶性转化为对偶问题,这可以使得求解过程更高效,尤其在高维空间中。
总之,SVM通过找到一个最大化分类间隔的超平面,利用支持向量和核函数等方法,实现了对线性和非线性分类问题的有效解决。其模型原理基于凸优化和最大间隔思想,使得它在许多实际问题中都表现出色。
2.模型参数
SVC类的构造函数可以接受多个参数来配置支持向量机模型的行为。以下是一些常用的参数及其说明:
-
C: 正则化参数,控制了决策边界的平衡,较小的值会使模型倾向于更大的边界,较大的值会使模型尽量正确分类每个样本。默认为1.0。
-
kernel: 核函数,用于将数据映射到高维空间。常见的核函数包括’linear’(线性核)、‘poly’(多项式核)、‘rbf’(高斯核)等。默认为’rbf’。
-
degree: 当使用多项式核函数时,表示多项式的次数。默认为3。
-
gamma: 核函数系数,控制了数据点的影响范围。对于’rbf’和’poly’核函数,较小的gamma值将导致决策边界平滑,较大的值将导致决策边界适应训练数据。默认为’scale’,即1 / (n_features * X.var())。
-
coef0: 核函数的独立项,在’poly’和’sigmoid’核函数中使用。默认为0.0。
-
shrinking: 是否使用收缩启发式算法来加速训练。默认为True。
-
probability: 是否启用概率估计。默认为False。
-
tol: 停止优化的容忍度。默认为1e-3。
-
class_weight: 类别权重,用于处理不平衡数据集。
-
verbose: 控制模型的详细程度。默认为False。
以下是使用SVC构造函数的一个例子:
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 加载Iris数据集
iris = load_iris()
X = iris.data
y = iris.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建SVM模型
model = SVC(C=1.0, kernel='linear', gamma='scale')
# 在训练集上训练模型
model.fit(X_train, y_train)
# 在测试集上进行预测
y_pred = model.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
在这个例子中,我们加载了Iris数据集,然后使用SVC模型进行训练和预测。你可以根据你的数据和任务需求,调整不同的参数来获得更好的模型性能。
3.文件结构
![]()
iris.xlsx % 可替换数据集
Main.py % 主函数
4.Excel数据
![]()
5.下载地址
- 资源下载地址
6.完整代码
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score, confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns
def svm_classification(data_path, test_size=0.2, random_state=42):
# 加载数据
data = pd.read_excel(data_path)
# 分割特征和标签
X = data.iloc[:, :-1] # 所有列除了最后一列
y = data.iloc[:, -1] # 最后一列
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
# 创建SVM模型
# 1. ** C: ** 正则化参数,控制了决策边界的平衡,较小的值会使模型倾向于更大的边界,较大的值会使模型尽量正确分类每个样本。默认为1.0。
# 2. ** kernel: ** 核函数,用于将数据映射到高维空间。常见的核函数包括'linear'(线性核)、'poly'(多项式核)、'rbf'(高斯核)等。默认为'rbf'。
# 3. ** degree: ** 当使用多项式核函数时,表示多项式的次数。默认为3。
# 4. ** gamma: ** 核函数系数,控制了数据点的影响范围。对于'rbf'和'poly'核函数,较小的gamma值将导致决策边界平滑,较大的值将导致决策边界适应训练数据。
# 默认为'scale',即1 / (n_features * X.var())。
# 5. ** coef0: ** 核函数的独立项,在'poly'和'sigmoid'核函数中使用。默认为0.0。
# 6. ** shrinking: ** 是否使用收缩启发式算法来加速训练。默认为True。
# 7. ** probability: ** 是否启用概率估计。默认为False。
# 8. ** tol: ** 停止优化的容忍度。默认为1e - 3。
# 9. ** class_weight: ** 类别权重,用于处理不平衡数据集。
# 10. ** verbose: ** 控制模型的详细程度。默认为False。
model = SVC(C=1.0, kernel='linear', gamma='scale')
# 在训练集上训练模型
model.fit(X_train, y_train)
# 在测试集上进行预测
y_pred = model.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
return confusion_matrix(y_test, y_pred), y_test.values, y_pred, accuracy
if __name__ == "__main__":
# 使用函数进行分类任务
data_path = "iris.xlsx"
confusion_mat, true_labels, predicted_labels, accuracy = svm_classification(data_path)
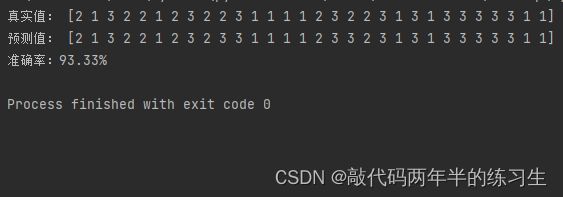
print("真实值:", true_labels)
print("预测值:", predicted_labels)
print("准确率:{:.2%}".format(accuracy))
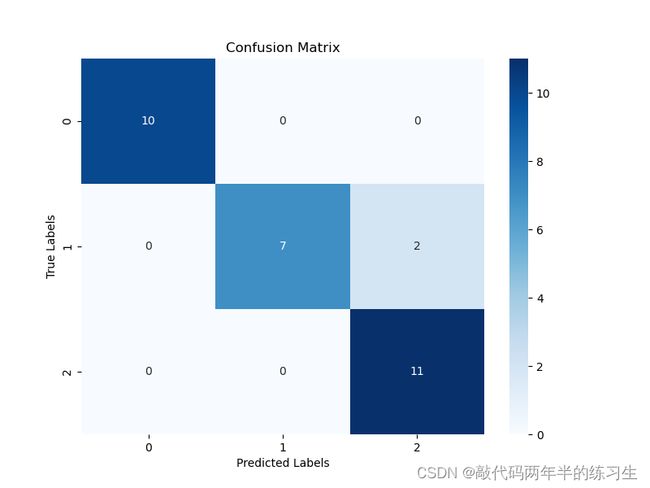
# 绘制混淆矩阵
plt.figure(figsize=(8, 6))
sns.heatmap(confusion_mat, annot=True, fmt="d", cmap="Blues")
plt.title("Confusion Matrix")
plt.xlabel("Predicted Labels")
plt.ylabel("True Labels")
plt.show()
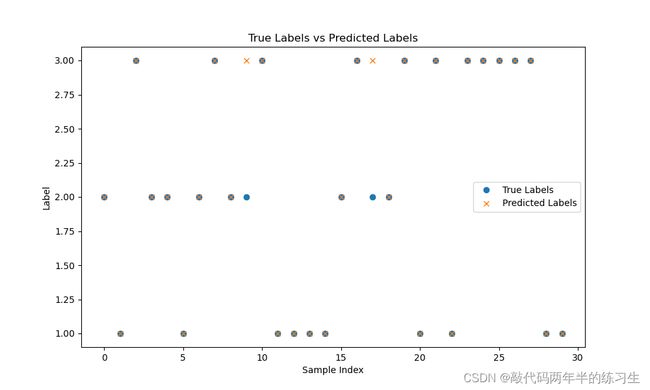
# 用圆圈表示真实值,用叉叉表示预测值
# 绘制真实值与预测值的对比结果
plt.figure(figsize=(10, 6))
plt.plot(true_labels, 'o', label="True Labels")
plt.plot(predicted_labels, 'x', label="Predicted Labels")
plt.title("True Labels vs Predicted Labels")
plt.xlabel("Sample Index")
plt.ylabel("Label")
plt.legend()
plt.show()