＜ 数据结构 ＞ 堆的应用 --- 堆排序和Topk问题

目录

1、堆排序

      法一：自己写堆进行排序

              时间复杂度分析

      法二：直接对数组建堆

              ①、向上调整建堆

              ②、向下调整建堆

              向上建堆和向下建堆熟优？

              升序能否建小堆？

              排序（建大堆）

2、TopK问题

        何为Topk？

        实现过程

---

1、堆排序

• 假如我们有一串乱序数组，如下：

 现在想要对它进行排序，按照我们之前学过的知识，想要单纯的实现排序其实并不难，可以直接暴力排序，也可以冒泡排序，甚至使用库函数qsort进行排序……

但是，既然近期学习了堆，那么堆的一个重要应用就是进行堆排序，这里先简要提下：堆排序即快排的一种。在后面的学习中，我将为大家继续展开其它更多样的快排。今儿个就向各位浅谈下快排之一：堆排序

法一：自己写堆进行排序

• 思路：

在上篇博文中，我们模拟实现了堆，实现后即可对一串乱序数组进行堆排序。假设我们排升序，且堆为小根堆。实现过程非常简单。

1. 首先，把数组的每个元素（HeapPush）插入到堆中。
2. 其次，我们深知小根堆的堆顶是最小的数字，依次遍历堆顶（HeapTop）的元素，将堆顶元素赋值到数组里，从下标0开始，赋值后删除（HeapPop）堆顶元素，++数组下标。此时堆就会重新调整，最终堆顶依旧是最小的，再重复上述赋值堆顶到数组的操作，直到堆为空（HeapEmpty）

• 代码如下：

//堆排序 --- 升序
void HeapSort(int* a, int size)
{
//创建堆结构并初始化
	HP hp; 
	HeapInit(&hp);
//将数组元素插入堆中
	for (int i = 0; i < size; i++)
	{
		HeapPush(&hp, a[i]);
	}
	size_t j = 0;
//依次遍历，取堆顶赋值数组，++下标，pop堆顶，依次循环，直至堆为空
	while (!HeapEmpty(&hp))
	{
		a[j] = HeapTop(&hp);
		j++;
		HeapPop(&hp);
	}
//记得销毁动态开辟空间
	HeapDestroy(&hp);
}
int main()
{
	int a[] = { 4,2,7,8,5,1,0,6 };
	HeapSort(a, sizeof(a) / sizeof(int)); //实现堆排序
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", a[i]); //打印
	}
	printf("\n");
	return 0;
}

• 效果如下：

时间复杂度分析

• 段一：

	for (int i = 0; i < size; i++)
	{
		HeapPush(&hp, a[i]);
	}

此段代码的时间复杂度为O(N*logN)，因为HeapPush函数的内部执行过程就是把数组的每个元素插入堆中，有N次。接着，每插入一个数据都要重新向上调整（AdjustUp）高度次以确保为堆，每个都要调整高度次，高度为logN，综上此段为O(N*logN)

• 段二：

	while (!HeapEmpty(&hp))
	{
		a[j] = HeapTop(&hp);
		j++;
		HeapPop(&hp);
	}

此段的时间复杂度同样为O(N*logN)，原理跟上一段类似，不过多赘述。

• 分析：

综上，时间复杂度为O(N*logN)，确实比我们先前的冒泡排序O(N^2)要快不少。但是，这个方法排序是及其不好的，因为难道说为了实现堆排序还要自己手写一个完整的堆吗？这么复杂的实现堆的过程还不如不用堆排序了，这种伤敌一千，自损八百的感脚实在是难受。更何况此法的空间复杂度也是很大的，达到了惊人的O(N)。原因是实现堆的过程是动态开辟的，所以空间复杂度自然是O(N)。可不可以换一更优的方法，但同样是利用堆的思想实现快排呢？

现在我们要求如下：

1. 依旧是堆的思想
2. 时间复杂度O(N*logN)
3. 空间复杂度O(1)

前面我们已经知晓，数组即为完全二叉树，为什么还要实现一个堆呢？直接把数组看作堆难道不香嘛？由此我们引出：直接对数组建堆。详解见下文：

法二：直接对数组建堆

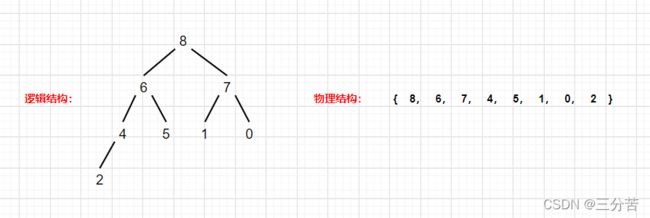
再来看下这串乱序数组：

既然上文说到可以直接把它看作二叉树，那不妨把逻辑结构画出来看看：

 

接下来，我们就要进行建堆了，有两种方法：

1. 使用向上建堆，插入数据的思想建堆
2. 使用向下调整建堆

①、向上调整建堆

• 思想：

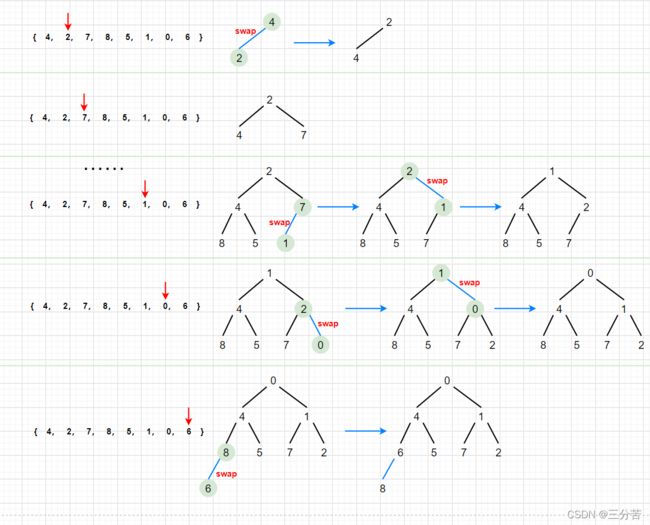
首先，我们把第一个数字看成堆，也就是4，当第二个数字插入进去的时候，进行向上调整算法，使其确保为小堆，向上调整的算法在上篇博文已详细讲解过，不过多赘述。具体插入数据过程就是遍历数组，确保数组里每一个数进行向上调整算法

• 画图演示：

•  代码如下：

//交换
void Swap(int* pa, int* pb)
{
	int tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}
//向上调整算法
void AdjustUp(int* a, size_t child)
{
	size_t parent = (child - 1) / 2;
	while (child > 0)
	{
		//if (a[child] > a[parent]) //大根堆
		if (a[child] < a[parent]) //小根堆
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
//升序
void HeapSort(int* a, int n)
{
	//建堆
	int i = 0;
	for (i = 1; i < n; i++) //应该从i=1时遍历，因为第一个数据在堆里不需要调整，后续再插入时调整
	{
		AdjustUp(a, i);
	}
}
int main()
{
	int a[] = { 4,2,7,8,5,1,0,6 };
	HeapSort(a, sizeof(a) / sizeof(int));
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", a[i]);
	}
	return 0;
}

•  效果如下：

 符合小堆的性质

②、向下调整建堆

• 问题：能直接进行向下建堆吗？

答案：不能

解析：首先回顾下使用向下调整的前提是什么？必须得确保根结点的左右子树均为小堆才可，而这里，数组为乱序的，无法直接使用。

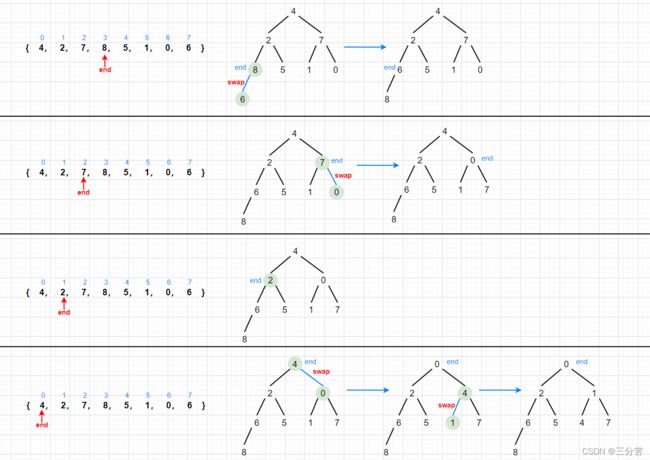
• 解决办法：从倒数第一个非叶结点开始向下调整，从下往上调

分析：从该解决方案中，我们首先要找到这个倒数第一个非叶结点的数在哪？其实最后一个结点的父亲即为倒数第一个非叶结点。当我们找到这个非叶结点时，把它和它的孩子看成一个整体，进行向下调整。调整后，再将次父节点向前挪动，再次向下调整，依次循环下去。

• 再回顾下父亲和孩子间的关系：

1. leftchild = parent*2 + 1
2. rightchild = parent*2 + 2
3. parent = (child - 1) / 2

• 画图解析过程：

•  代码如下：

//升序
void HeapSort(int* a, int n)
{
	//建堆
	//1、向上调整
	int i = 0;
	for (i = 1; i < n; i++) //应该从i=1时遍历，因为第一个数据在堆里不需要调整，后续再插入时调整
	{
		AdjustUp(a, i);
	}
	//2、向下调整
	for (int i = (n - 1 - 1)/2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
}

• 效果如下：

 符合小堆的性质

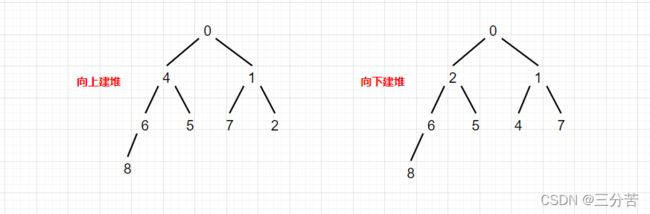
向上建堆和向下建堆熟优？

• 首先，我们画张图看下向上和向下建堆后的样子。

从上图中，我们可以看出，使用不同的方式建堆最后的样子是不同的，那哪种方式好呢？

• 接下来，我将通过时间复杂度的方式为大家解惑：以一颗满二叉树为例：

•  向上建堆：

时间复杂度计算的是其调整的次数，根据上文的知识我们已经知晓其是从数组的第二个元素开始的，也就是可以理解为第二层的第一个节点。计算的思想非常简单：计算每层有多少个节点乘以该层的高度次，然后累计相加即可。如下：

通过计算得知：向上建堆的时间复杂度为O(N*logN)

• 向下建堆：

向下调整我们前面已经知道它是从倒数第1个非叶节点开始调整的，每层的调整次数为，该层的节点个数*该层高度减1，一直从第1层开始调直至倒数第2层，并将其依次累加，此计算过程和向上调整差不多，都是等比*等差的求和，过程如下：

 通过计算得知：向下建堆的时间复杂度为O(N)

• 对比：

通过上述计算，我们得到如下：

1. 向上建堆：O(N*logN)
2. 向下建堆：O(N)

由此可见，使用向下建堆的方式更优，其时间复杂度较小。当然，使用向上建堆也是可以的，只不过向下建堆更好一点。

升序能否建小堆？

• 答案：不能

解析：

从上文我们已经知道建堆用向下建堆是比较优的，为O(N)，并且建好堆后第一个位置的数字即为最小的，此时第一个数字已经确定了并且是最小的，但如若使用小堆的话，也就是需要从第二个数字开始往后看成一个堆，此时关系就全乱了，不再符合小堆的性质，此时也就意味着我们需要从第二个数字往后重新向下建堆，以确保此时的堆顶也就是数组第二个元素为次小的，并以此类推重新建堆确保第三个次小的，依次循环下去……如果这样做，还不如直接遍历选数！搞这么复杂。

• 解决方案：升序建大堆

排序（建大堆）

•  先看下建好大堆的样子：

• 思路：

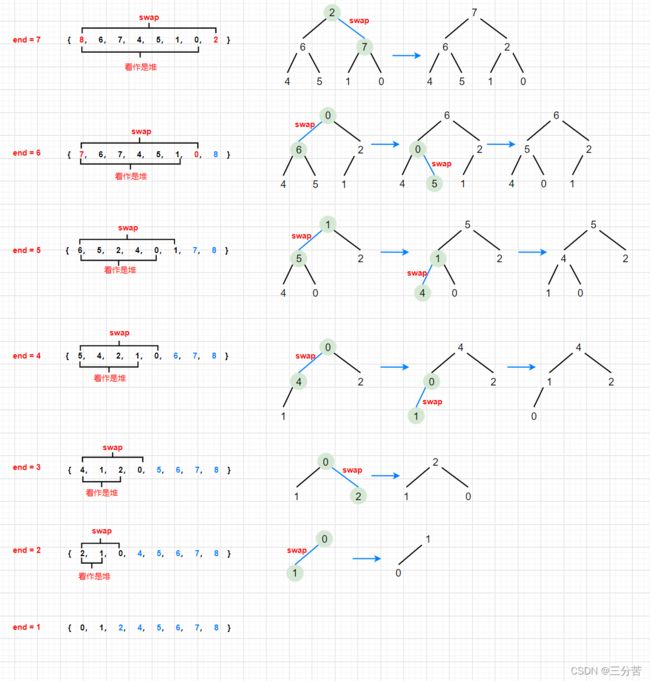
首先，得明确我们建堆后，此时堆顶就是最大的数据，现在我们把第一个数字和最后一个数字交换，把最后一个数字不看做堆里的，只需要数组个数N--即可。此时的左子树和右子树依旧是大堆，再进行向下调整即可。

• 画图解析过程：

• 代码如下：

//交换
void Swap(int* pa, int* pb)
{
	int tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}
//向下调整算法
void AdjustDown(int* a, size_t size, size_t root)
{
	int parent = (int)root;
	int child = 2 * parent + 1;
	while (child < size)
	{
		//1、确保child的下标对应的值最大，即取左右孩子较大那个
		if (child + 1 < size && a[child + 1] > a[child]) //得确保右孩子存在
		{
			child++; //此时右孩子大
		}
		//2、如果孩子大于父亲则交换，并继续往下调整
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}
//升序
void HeapSort(int* a, int n)
{
	//向下调整建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	//大堆升序
	size_t end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}
int main()
{
	int a[] = { 4,2,7,8,5,1,0,6 };
	HeapSort(a, sizeof(a) / sizeof(int));
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", a[i]);
	}
	return 0;
}

•  效果如下：

2、TopK问题

何为Topk？

• TOP-K问题：N个数里面找出最大/最小的前k个。一般情况下数据量都比较大。

比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

对于Top-K问题，我们能想到的方法有很多，如下：

1. 排序 -- 时间复杂度：O(N*logN)。 空间复杂度：O(1) -- 要求进一步优化。
2. 建立N个数的大堆，Pop K次，就可以找出最大的前K个 -- 时间复杂度：O(N+logN*k)。空间复杂度：O(1)

• 问题：

有可能N非常大，以至于远大于K。比如100亿个数里面找出最大的前10个。此时上面的方法就不能用了，因为此时会导致内存不够。就好比我现在想知道100亿个整数需要多少空间？

• 1G = 1024MB
• 1024MB = 1024*1024KB
• 1024*1024KB = 1024*1024*1024Byte ≈ 10亿字节
• 一个整数4个字节，100亿个整数400亿个字节，≈40G

40个G内存根本放不下，说明100亿个整数是放在磁盘中的，也就是文件中。由此得知上述方法不得行，得寻找一个更优解。

• 解决方案：

用前K个数建立一个K个数的小堆，然后剩下的N-K个依次遍历，如果比堆顶的数据大，就替换它进堆（向下调整），最后堆里面的K个数就是最大的K个。

• 复杂度：

1. 时间复杂度：O(K + logK * (N-K))
2. 空间复杂度：O(K)

实现过程

以从1w个数里找出最大的前10个数为例：

//向下调整算法
void AdjustDown(int* a, size_t size, size_t root)
{
	int parent = (int)root;
	int child = 2 * parent + 1;
	while (child < size)
	{
		//1、确保child的下标对应的值最小，即取左右孩子较小那个
		if (child + 1 < size && a[child + 1] < a[child]) //得确保右孩子存在
		{
			child++; //此时右孩子大
		}
		//2、如果孩子小于父亲则交换，并继续往下调整
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}
void PrintTopK(int* a, int n, int k)
{
	// 1. 建堆--用a中前k个元素建堆
	int* kminHeap = (int*)malloc(sizeof(int) * k);
	assert(kminHeap);
	for (int i = 0; i < k; i++)
	{
		kminHeap[i] = a[i];
	}
	//建小堆
	for (int j = (k - 1 - 1) / 2; j >= 0; j--)
	{
		//从倒数第一个非叶节点开始
		AdjustDown(a, k, j);
	}
	// 2. 将剩余n-k个元素依次与堆顶元素交换，不满则则替换
	for (int i = k; i < n; i++)
	{
		if (a[i] > kminHeap[0])
		{
			kminHeap[0] = a[i]; //如果比堆顶大，就替换
			AdjustDown(kminHeap, k, 0); //向下调整确保为堆
		}
	}
	for (int j = 0; j < k; j++)
	{
		printf("%d ", kminHeap[j]);
	}
	printf("\n");
	free(kminHeap);
}
void TestTopk()
{
	int n = 10000;
	int* a = (int*)malloc(sizeof(int) * n);
	srand(time(0));
	for (size_t i = 0; i < n; ++i)
	{
		a[i] = rand() % 1000000; //产生一个随机数，数值均小于100万
	}
	a[5] = 1000000 + 1;
	a[1231] = 1000000 + 2;
	a[531] = 1000000 + 3;
	a[5121] = 1000000 + 4;
	a[115] = 1000000 + 5;
	a[2335] = 1000000 + 6;
	a[9999] = 1000000 + 7;
	a[76] = 1000000 + 8;
	a[423] = 1000000 + 9;
	a[3144] = 1000000 + 10;
	PrintTopK(a, n, 10);
}

int main()
{
	TestTopk();
	return 0;
}

• 效果如下：