【数学建模+数据处理类】2021数学建模国赛B题 乙醇偶合制备C4烯烃
文章目录
- 问题一
- 问题二
- 问题三
- 问题四
- 灵敏度分析
问题一
对附件1中每种催化剂组合，分别研究乙醇转化率、C4烯烃的选择性与温度的关系，并对附件2中350度时给定的催化剂组合在一次实验不同时间的测试结果进行分析。
step1：对实验数据进行探索性分析
- 数据的预处理（A11的缺失）
- 可视化、数据关系展示
包括画出各个因变量（不同催化剂作用下乙醇转化率、C4烯烃选择性、收率）与温度的散点图等，例如对于A5
step2：对不同催化剂作用下乙醇转化率、C4烯烃的选择性与温度进行相关分析，说明其显著性
| 变量 | 描述含义 |
|---|---|
| Y1 | 乙醇转化率 |
| Y2 | C4烯烃选择性 |
| X1 | Co负载量 |
| X2 | Co/Sio2和HA P的装料比 |
| X3 | 乙醇浓度 |
| X4 | 温度 |
由于因变量的数值都是百分数为单位所以为其做相应的Logit变换：
y = l o g [ y % / ( 1 − y % ) ] y=log[y\%/(1-y\%)] y=log[y%/(1−y%)]
x4=[250.00 275.00 300.00 325.00 350.00 ];
y1=[-0.760619463 -0.848123231 -0.580435779 -0.402686952 -0.234653057];
corrcoef(x4,y1)
求得x4与y1（变换后）的相关系数为0.939，得到结论两者相关系显著。
各个因变量与温度间的关联分析，非线性影响、显著性检验等。
灰色关联度结果，例如：
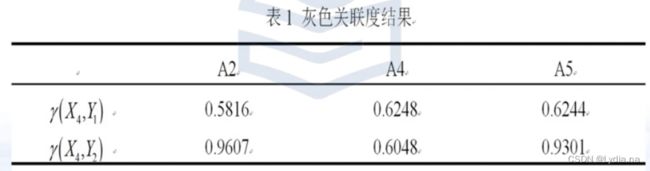
step3：尝试多种拟合模型，选择较优的拟合函数，并得到乙醇转化率、C4烯烃的选择性与温度的函数关系
观察并确定所要拟合的模型曲线形式，优化计算出模型拟合值。如：线性、二次、指数、logit变换线性，参数估计等。
经比较计算logit变换一次或二次模型是较好的选择，参数少而显著，平均 R 2 R^2 R2较高。
根据以上研究可以认为，乙醇转化率C4烯烃选择性与温度具有二次相关，且为正相关。
step4：对给定催化剂在温度350摄氏度的情况下进行稳定性分析。即随着时间变化，乙醇转化率、C4烯烃选择性、收率变化规律的稳定性分析。
可用方差分析、logit变换或均值模型残差的方差是否减少。结果趋于稳定。
如果用某类函数（比如参数超过3个多项式等）直接拟合得到的关系，且没有进行误差分析，则是不好的做法。
问题二
探讨不同催化剂组合及温度对乙醇转化率以及C4烯烃选择性大小的影响。
step1：不同乙醇浓度、Co的负载量、装料比和温度对乙醇转化率、C4烯烃选择性的大小影响程度。
百分数（转化率、选择性）数据直接用线性模型难以描述，通常进行logit等变换，再建立回归模型来进行比较（方差分析），确定重要因素。
step2:全因素方差分析（方差分析表，F-检验，显著水平0.05）
表明：温度>乙醇浓度
这两个因素同时对Y1和Y2产生显著影响。
step3：对自变量进行主成分回归分析
各反应物、催化剂、反应条件之间可能存在着共线性关系，方差扩大因子数过大，故将存在共线性关系的自变量进行主成分回归分析，得出聚合后自变量因子进行多元线性回归。
step4：进行多元逐步回归分析
由于直接利用上述指标探究对乙醇转化率和C4烯烃选择性进行分析会造成信息重叠，形成偏差，所以采用多元线性回归进行分析。
step5：求解回归系数及分析
step6：误差分析
得知温度变量在解释两个乙醇转化率、C4烯烃回归方程中起到了极为重要的作用。
问题三
如何选择催化剂组合与温度，使得在相同实验条件下C4烯烃收率尽可能
高。若使温度低于350度，又如何选择催化剂组合与温度，使得C4烯烃收率尽可能高。
step1：建立烯烃收率的基础模型
目标函数确定： m a x = y 1 ∗ y 2 max=y_1*y_2 max=y1∗y2，其中y1为乙醇转化率，y2为C4烯烃选择性
约束条件确定： ∑ i = 1 5 y i = 100 \sum_{i=1}^{5}y_{i}=100 i=1∑5yi=100该式为所有生成物选择性之和等于百分之百
X l i ≤ x i ≤ X l r i = 1 , 2 , . . . , 5 Xl_i\le x_i\le Xl_ri=1,2,...,5 Xli≤xi≤Xlri=1,2,...,5该式为所有自变量满足已有实验设计的取值范围。根据问题二中对附件一进行的数据拆分，分析得到每一种自变量的实际取之范围。
step2：基于多元线性回归的模型优化
由于对于建立的烯烃收率的基础模型和题目给出的条件及数据，无法获得准确的约束条件对基础数学模型进行求解，经过测试无法直接利用上述的最优化模型进行求解。因此提出基于多元线性回归的C4烯烃最大收率模型。由于乙醇转化率和C3烯烃选择性两者的函数表达式来自于通过物种因变量的多元回归拟合，因此可以将y1,y2拆分得到多个自变量对C4烯烃收率进行多元回归分析，将拟合成的多元回归模型作为新一轮的目标函数，从而对原有模型进行有效改进。
step3：基于方差分析的C4烯烃收率模型优化
对于C4烯烃收率来说，受到了乙醇转化率与C4烯烃转化率的系数的直接限制，因此引入方差分析，来看两个变量之间是否含有相互作用关系，从而来对C4烯烃的单目标模型进行优化。
问题四
如果允许再增加5次实验，应如何设计，并给出详细理由。
该问题使用了均匀试验设计方法
相较于正交设计，均匀试验设计适用于水平多，因素少的数据，并且均匀试验设计由于只考虑试验点在试验范围内的均匀散布，减少了进行试验次数，且更加合适在较少的试验中获得更多信息。
灵敏度分析
由问题二克制，温度等自变量对因变量的变化有强烈影响，因此通过对C4烯烃收率的回归方程中的温度系数进行灵敏度分析，使其值经过上下百分之5的数据波动。