8.14 刷题【7道】
二叉树
1. 树中两个结点的最低公共祖先
原题链接
![]()
方法一:公共路径
分别找出根节点到两个节点的路径,则最后一个公共节点就是最低公共祖先了。
时间复杂度分析:需要在树中查找节点,复杂度为O(n)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int findPath(TreeNode*root, TreeNode* p, vector<TreeNode*>&path){
if(!root)
return 0;
if(root->val==p->val){
path.push_back(root);
return 1;
}
int l = findPath(root->left,p,path);
int r = findPath(root->right,p,path);
if(l==1||r==1)
path.push_back(root);
return l==1||r==1;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
vector<TreeNode*>path1,path2;
findPath(root,p,path1);
findPath(root,q,path2);
if(path1.empty()||path2.empty())
return NULL;
TreeNode* res =NULL;
for(int i = 0;i<path1.size();i++){
if(i>=path1.size()||i>=path2.size())
break;
if(path1[path1.size()-1-i]==path2[path2.size()-1-i])
res = path1[path1.size()-1-i];
else
break;
}
return res;
}
};
方法二:递归
考虑在左子树和右子树中查找这两个节点,如果两个节点分别位于左子树和右子树,则最低公共祖先为自己(root),若左子树中两个节点都找不到,说明最低公共祖先一定在右子树中,反之亦然。考虑到二叉树的递归特性,因此可以通过递归来求得。
时间复杂度分析:需要遍历树,复杂度为 O(n)
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(!root)
return NULL;
if(root==p||root==q)
return root;
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if(left&&right)
return root;
if(left==NULL)
return right;
else
return left;
}
};
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean flag = false;
public TreeNode ans = null;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
dfs(root,p,q);
return ans;
}
public TreeNode dfs(TreeNode root,TreeNode p,TreeNode q){
if(root == null){
return null;
}
TreeNode l = dfs(root.left,p,q);
TreeNode r = dfs(root.right,p,q);
if(l != null && r != null){
ans = root;
return ans;
} else if((l != null || r != null) && (root.val == p.val || root.val == q.val)){
ans = root;
return ans;
} else if(root.val == p.val && root.val == q.val) {
ans = root;
return ans;
} else if(root.val == p.val || root.val == q.val) {
return root;
} else if((l != null || r != null)){
return root;
}
return null;
}
}
2. 重建二叉树
原题链接
![]()
根据前序遍历和中序遍历 得到树
过程如下:
- 首先根据前序遍历找到 根节点
- 找到中序遍历中,该根节点的位置
- 中序中 位于 根节点左边的就是 左子树,右边的就是右子树
- 由于我们需要在中序遍历中找到根节点的位置,那么每次都需要遍历中序遍历,不如直接用unordered_map存储数值和位置
- 便于写代码,我们可以每次把mp[根节点] 的位置 用变量表示出来
![]()
本题的代码不需要死记硬背
就需要明白
由前序确定根节点
由中序确定左右子树的个数
由左右子树的个数确定下一个根节点的位置
根据这三点去写代码即可
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
unordered_map<int,int> pos;
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n = preorder.size();
for (int i = 0; i < n; i ++ )
pos[inorder[i]] = i;
return dfs(preorder, inorder, 0, n - 1, 0, n - 1);
}
TreeNode* dfs(vector<int>&pre, vector<int>&in, int pl, int pr, int il, int ir)
{
if (pl > pr) return NULL;
int k = pos[pre[pl]] - il;
TreeNode* root = new TreeNode(pre[pl]);
root->left = dfs(pre, in, pl + 1, pl + k, il, il + k - 1);
root->right = dfs(pre, in, pl + k + 1, pr, il + k + 1, ir);
return root;
}
};
补充题:树的遍历
![]()
![]()
![]()
![]()
#include 3. 二叉树的下一个节点
原题链接
中序遍历:左根右
![]()
本题要分析节点的特点
- 如果节点有右子树,那么右子树的最左边的节点就是该节点后序
- 如果没有右子树,会有三种可能,在代码中有体现
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode father;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
/**
* 模拟
* 时间复杂度:O(height),height 为二叉树的高度
* 空间复杂度:O(1)
*/
public TreeNode inorderSuccessor(TreeNode p) {
TreeNode node = p;
// Case 1. 如果该节点有右子树,那么下一个节点就是其右子树中最左边的节点
if (node.right != null) {
node = node.right;
while (node.left != null) {
node = node.left;
}
return node;
}
if(node.father != null && node.father.left == node)
return node.father;
if(node.father != null && node.father == null)
return null;
while(node.father!=null && node.father.right == node)
{
node = node.father;
}
return node.father;
}
}
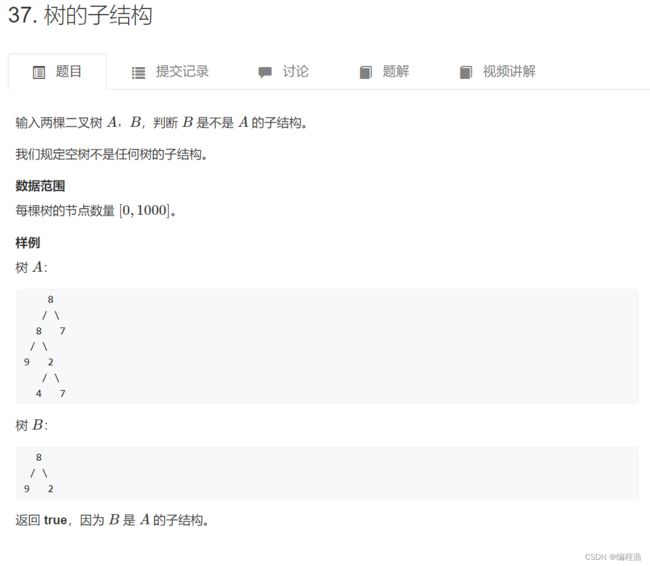
4. 树的子结构( 递归中调用递归 )
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool hasSubtree(TreeNode* pRoot1, TreeNode* pRoot2) {
if (!pRoot1 || !pRoot2) return false;
if (isSame(pRoot1, pRoot2)) return true;
return hasSubtree(pRoot1->left, pRoot2) || hasSubtree(pRoot1->right, pRoot2);
}
bool isSame(TreeNode* pRoot1, TreeNode* pRoot2) {
if (!pRoot2) return true;
if (!pRoot1 || pRoot1->val != pRoot2->val) return false;
return isSame(pRoot1->left, pRoot2->left) && isSame(pRoot1->right, pRoot2->right);
}
};
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean hasSubtree(TreeNode pRoot1, TreeNode pRoot2) {
// 类比字符串匹配
if (pRoot1 == null || pRoot2 == null) return false;
if (isPart(pRoot1, pRoot2)) return true;
// 如果以 pRoot1 开始的子树不能包含 pRoot2 的话,就从 pRoot1.left 和 pRoot1.right 开始
return hasSubtree(pRoot1.left, pRoot2) || hasSubtree(pRoot1.right, pRoot2);
}
// 以 pRoot1 节点为根的情况下,pRoot1 和 pRoot2 同时对应遍历,如果遍历到的值都相同,且 pRoot2 先遍历到 null 或者同时遍历到 null,说明 pRoot2 是 pRoot1 的子结构
public boolean isPart(TreeNode pRoot1, TreeNode pRoot2) {
if (pRoot2 == null) return true;
if (pRoot1 == null || pRoot1.val != pRoot2.val) return false;
// 同时遍历左右子树
return isPart(pRoot1.left, pRoot2.left) && isPart(pRoot1.right, pRoot2.right);
}
}
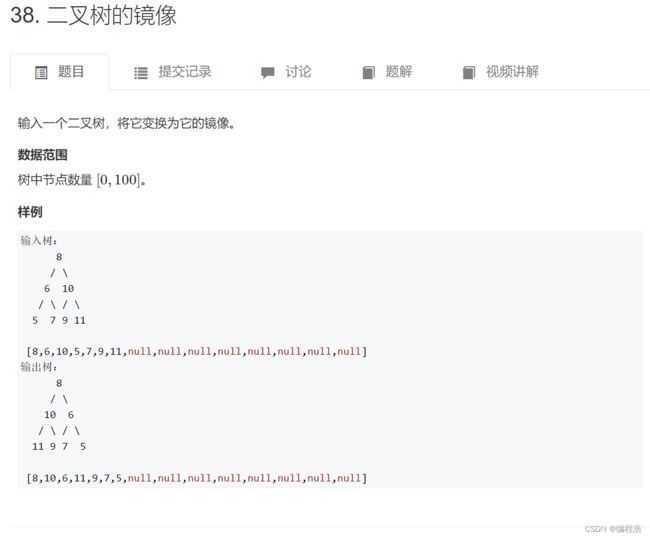
5. 二叉树的镜像(两个指针互换可用 swap)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
void mirror(TreeNode* root) {
if (!root) return;
swap(root->left, root->right);
mirror(root->left);
mirror(root->right);
}
};
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public void mirror(TreeNode root) {
dfs(root);
}
public void dfs(TreeNode root){
if(root == null){
return;
}
TreeNode temp = root.right;
root.right = root.left;
root.left = temp;
dfs(root.left);
dfs(root.right);
}
}
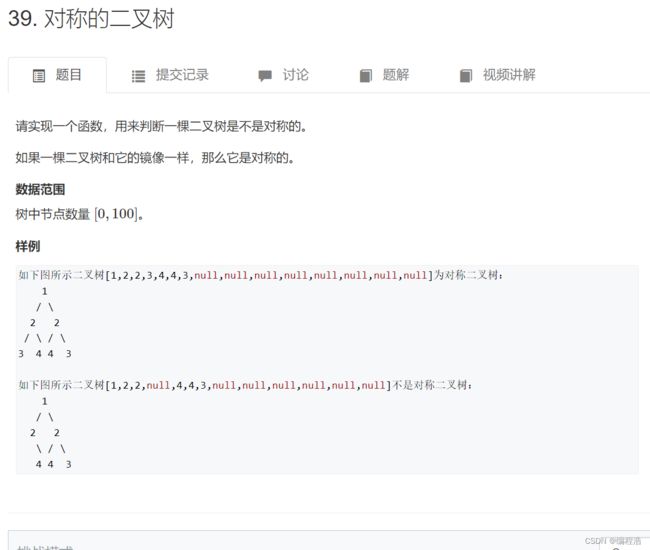
6. 对称的二叉树
错解:通过根节点比较子节点
没写完,太复杂
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(root == NULL)
return true;
return dfs(root->left,root->right);
}
bool dfs(TreeNode* r1,TreeNode* r2)
{
if(r1==NULL && r2==NULL)
return true;
if(r1!=NULL&&r2==NULL || r1==NULL&&r2!=NULL)
return false;
if(r1->left->val != r2->right->val || r1->right->val != r2->left->val)
return false;
return dfs(r1->left,r2->right) && dfs(r1->right,r2->left);
}
};
正解:比较当前节点的值即可
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(root == NULL)
return true;
return dfs(root->left,root->right);
}
bool dfs(TreeNode* r1,TreeNode* r2)
{
if(r1==NULL && r2==NULL)
return true;
if(r1!=NULL&&r2==NULL || r1==NULL&&r2!=NULL)
return false;
if(r1->val != r2->val)
return false;
return dfs(r1->left,r2->right) && dfs(r1->right,r2->left);
}
};
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root == null){
return true;
}
return dfs(root.left,root.right);
}
public boolean dfs(TreeNode l,TreeNode r){
if((l == null && r != null) || (l != null && r == null)){
return false;
}
if(l == null && r == null){
return true;
}
if(l.val != r.val){
return false;
}
return dfs(l.left,r.right) && dfs(l.right,r.left);
}
}
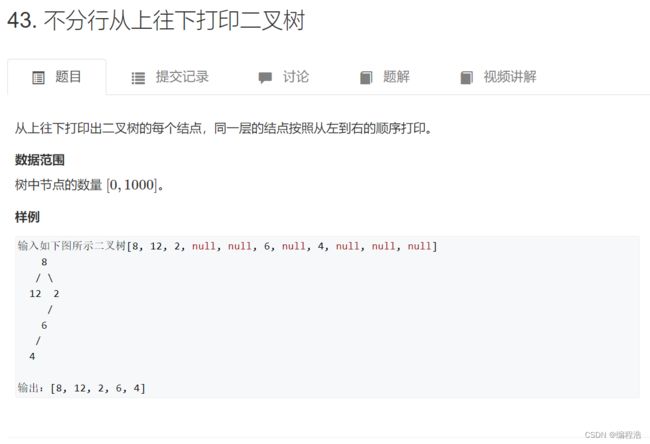
7. 不分行从上往下打印二叉树( 层序遍历二叉树bfs )
原题链接
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> printFromTopToBottom(TreeNode* root) {
vector<int> ans;
if(root==NULL)
return ans;
queue<TreeNode*> q;
q.push(root);
while(q.size())
{
auto t = q.front();
q.pop();
ans.push_back(t->val);
if(t->left != NULL)
q.push(t->left);
if(t->right != NULL)
q.push(t->right);
}
return ans;
}
};