多种求组合数算法
目录
- 求组合数Ⅰ(递推)
-
- 核心理论
- 理论推导
- 典型例题
-
- 代码实现
- 求组合数Ⅱ(预处理)
-
- 核心理论
- 典型例题
-
- 代码实现
- 求组合数Ⅲ(Lucas定理)
-
- 核心理论
- Lucas定理的证明
-
- 1.证明Lucas定理的第一形式
- 2.证明Lucas定理的第二形式
- 典型例题
-
- 代码实现
- 求组合数Ⅳ(高精度乘法及质因子优化)
-
- 核心理论
- 典型例题
-
- 代码实现
- 求组合数Ⅴ(卡特兰数)
-
- 卡特兰数的概念
- 卡特兰数的应用场景
- 满足条件的01序列
-
- 利用卡特兰数求解
- 代码实现
求组合数Ⅰ(递推)
适合场景: 1 ≤ b ≤ a ≤ 2000 1\leq b \leq a \leq2000 1≤b≤a≤2000,取模情况下。
核心理论
C a b = C a − 1 b + C a − 1 b − 1 \large C_a^b=C_{a-1}^b+C_{a-1}^{b-1} Cab=Ca−1b+Ca−1b−1
通过递推的方式来求解。
理论推导
先把 a a a 个元素分成两个部分:
- 第 a a a 个元素
- 剩下的 a − 1 a-1 a−1 个元素
在选择 b b b 个元素时,有两种情况:
- 选取第 a a a 个元素
- 不选取第 a a a 个元素
如果选取第 a a a 个元素,那么我们需要从剩下的 a − 1 a-1 a−1 个元素中选择 b − 1 b-1 b−1 个元素。由组合数定义,这种情况的个数为 C a − 1 b − 1 C_{a-1}^{b-1} Ca−1b−1。
如果不选取第 a a a 个元素,那么我们需要从剩下的 a − 1 a-1 a−1 个元素中选择 b b b个元素。这种情况的个数为 C a − 1 b C_{a-1}^b Ca−1b。
于是总的组合个数就等于上面两种情况之和:
C a b = C a − 1 b − 1 + C a − 1 b C_a^b = C_{a-1}^{b-1} + C_{a-1}^b Cab=Ca−1b−1+Ca−1b
典型例题
题目描述:
给定 n n n 组询问,每组询问给定两个整数 a , b a,b a,b,请你输出 C a b ( m o d 1 0 9 + 7 ) C_a^b \pmod {10^9+ 7} Cab(mod109+7)的值。
输入格式:
第一行包含整数 n n n。
接下来 n n n 行,每行包含一组 a a a 和 b b b。
输出格式:
共 n n n 行,每行输出一个询问的解。
数据范围:
1 ≤ n ≤ 10000 1 \leq n \leq 10000 1≤n≤10000
1 ≤ b ≤ a ≤ 2000 1 \leq b \leq a \leq 2000 1≤b≤a≤2000
输入样例:
3
3 1
5 3
2 2
输出样例:
3
10
1
代码实现
#define _CRT_SECURE_NO_WARNINGS
#include求组合数Ⅱ(预处理)
核心理论
适合场景: 1 ≤ b ≤ a ≤ 1 0 5 1 \leq b \leq a \leq 10^5 1≤b≤a≤105,取模情况下。
C a b = a ! ( a − b ) ! ∗ b ! \large C_a^b=\frac{a!}{(a-b)! * b!} Cab=(a−b)!∗b!a!
由于数据较大且可取模,因此通过求乘法逆元的方法来将 a ! ( a − b ) ! ∗ b ! \frac{a!}{(a-b)! * b!} (a−b)!∗b!a! 转换为 a ! ∗ b ! ∗ ( a − b ) ! − 1 a! * b! * {(a-b)!}^{-1} a!∗b!∗(a−b)!−1 的形式。
因此采用两个数组来递推:
f a c t [ i ] = i ! % m o d fact[i] = i!\ \% \ mod fact[i]=i! % mod
i n f a c t [ i ] = ( i ! ) − 1 % m o d infact[i] = (i!)^{-1}\ \% \ mod infact[i]=(i!)−1 % mod
C a b = a ! ( a − b ) ! ∗ b ! = ( f a c t [ a ] ∗ i n f a c t [ a − b ] ∗ i n f a c t [ b ] ) \large C_a^b=\frac{a!}{(a-b)! * b!} = (fact[a] * infact[a-b] * infact[b] )\ % \ mod Cab=(a−b)!∗b!a!=(fact[a]∗infact[a−b]∗infact[b])
典型例题
题目描述:
给定 n n n 组询问,每组询问给定两个整数 a , b a,b a,b,请你输出 C a b ( m o d 1 0 9 + 7 ) C_a^b \pmod {10^9+7} Cab(mod109+7)的值。
输入格式:
第一行包含整数 n n n。
接下来 n n n 行,每行包含一组 a a a 和 b b b。
输出格式:
共 n n n 行,每行输出一个询问的解。
数据范围:
1 ≤ n ≤ 10000 1 \leq n \leq 10000 1≤n≤10000
1 ≤ b ≤ a ≤ 1 0 5 1 \leq b \leq a \leq 10^5 1≤b≤a≤105
输入样例:
3
3 1
5 3
2 2
输出样例:
3
10
1
代码实现
#define _CRT_SECURE_NO_WARNINGS
#include求组合数Ⅲ(Lucas定理)
适合场景: 1 ≤ b ≤ a ≤ 1 0 18 1 \leq b \leq a \leq 10^{18} 1≤b≤a≤1018,取模且模数为在 1 ≤ p ≤ 1 0 5 1\leq p \leq 10^5 1≤p≤105 较小范围内的质数。
核心理论
Lucas(卢卡斯)定理:
1.Lucas定理的第一形式
C a b ≡ ∏ i = 0 k C b i a i ( m o d p ) \LARGE \begin{align*} C_a^b \equiv \prod_{i=0}^kC_{b_i}^{a_i}\pmod p \end{align*} Cab≡i=0∏kCbiai(modp)
其中:
- a = ∑ i = 0 k a i p i a=\sum_{i=0}^ka_ip^i a=∑i=0kaipi 和 b = ∑ i = 0 k b i p i b=\sum_{i=0}^kb_ip^i b=∑i=0kbipi 是 a a a 和 b b b 在素数 p p p 的 p p p 进制展开。
2.Lucas定理的第二形式
C a b ≡ C a % p b % p ∗ C a ÷ p b ÷ p ( m o d p ) \LARGE C_a^b \equiv C_{a\%p}^{b\%p} * C_{a \div p}^{b \div p} \pmod p Cab≡Ca%pb%p∗Ca÷pb÷p(modp)
Lucas定理的证明
1.证明Lucas定理的第一形式
2.证明Lucas定理的第二形式
典型例题
题目描述:
给定 n n n 组询问,每组询问给定三个整数 a , b , p a,b,p a,b,p,其中 p p p 是质数,请你输出 C a b ( m o d p ) C_a^b \pmod p Cab(modp) 的值。
输入格式:
第一行包含整数 n n n。
接下来 n n n 行,每行包含一组 a , b , p a,b,p a,b,p。
输出格式:
共 n n n 行,每行输出一个询问的解。
数据范围:
1 ≤ n ≤ 20 1 \leq n \leq 20 1≤n≤20
1 ≤ b ≤ a ≤ 1 0 18 1 \leq b \leq a \leq 10^{18} 1≤b≤a≤1018
1 ≤ p ≤ 1 0 5 1 \leq p \leq 10^5 1≤p≤105
输入样例:
3
5 3 7
3 1 5
6 4 13
输出样例:
3
3
2
代码实现
#define _CRT_SECURE_NO_WARNINGS
#include求组合数Ⅳ(高精度乘法及质因子优化)
适合场景: 1 ≤ b ≤ a ≤ 5000 1 \leq b \leq a \leq 5000 1≤b≤a≤5000,且不取模的情况下。
核心理论
C a b = a ! ( a − b ) ! ∗ b ! \large C_a^b=\frac{a!}{(a-b)! * b!} Cab=(a−b)!∗b!a!
由于不能取模,直接求阶乘会导致数据溢出。因此采用高精度乘法进行计算,但直接采用高精度乘法效率过低,因此采用分解质因子,将每个阶乘中的质因子出现个数计算出来,再利用高精度乘法来计算从而达到效率目的。
分解质因子:
C a b = p 1 α 1 × p 2 α 2 × p 3 α 3 . . . × p k α k \large C_a^b=p_1^{\alpha_1} \times p_2^{\alpha_2} \times p_3^{\alpha_3} ... \times p_k^{\alpha_k} Cab=p1α1×p2α2×p3α3...×pkαk
计算阶乘中某质因子出现的个数:
c n t a ! = ⌊ a p ⌋ + ⌊ a p 2 ⌋ + ⌊ a p 3 ⌋ + . . . + ⌊ a p k ⌋ \large cnt_{a!}=\lfloor \frac{a}{p} \rfloor + \lfloor \frac{a}{p^2} \rfloor + \lfloor \frac{a}{p^3} \rfloor + ...+ \lfloor \frac{a}{p^k} \rfloor cnta!=⌊pa⌋+⌊p2a⌋+⌊p3a⌋+...+⌊pka⌋
c n t b ! = ⌊ b p ⌋ + ⌊ b p 2 ⌋ + ⌊ b p 3 ⌋ + . . . + ⌊ b p k ⌋ \large cnt_{b!}=\lfloor \frac{b}{p} \rfloor + \lfloor \frac{b}{p^2} \rfloor + \lfloor \frac{b}{p^3} \rfloor + ...+ \lfloor \frac{b}{p^k} \rfloor cntb!=⌊pb⌋+⌊p2b⌋+⌊p3b⌋+...+⌊pkb⌋
c n t ( a − b ) ! = ⌊ a − b p ⌋ + ⌊ a − b p 2 ⌋ + ⌊ a − b p 3 ⌋ + . . . + ⌊ a − b p k ⌋ \large cnt_{(a-b)!}=\lfloor \frac{a-b}{p} \rfloor + \lfloor \frac{a-b}{p^2} \rfloor + \lfloor \frac{a-b}{p^3} \rfloor + ...+ \lfloor \frac{a-b}{p^k} \rfloor cnt(a−b)!=⌊pa−b⌋+⌊p2a−b⌋+⌊p3a−b⌋+...+⌊pka−b⌋
最后再利用高精度乘法对这些质因子进行乘法。
典型例题
题目描述:
输入 a , b a,b a,b,求 C a b C_a^b Cab 的值。
注意结果可能很大,需要使用高精度计算。
输入格式:
共一行,包含两个整数 a a a 和 b b b。
输出格式:
共一行,输出 C a b C_a^b Cab 的值。
数据范围:
1 ≤ b ≤ a ≤ 5000 1 \leq b \leq a \leq 5000 1≤b≤a≤5000
输入样例:
5 3
输出样例:
10
代码实现
#include 求组合数Ⅴ(卡特兰数)
卡特兰数的概念
卡特兰数( C a t a l a n n u m b e r Catalan number Catalannumber)是 组合数学 中一个常出现在各种 计数问题 中的 数列。
前几个卡特兰数依次为: 1 , 1 , 2 , 5 , 14 , 42 , 132 , 429 , 1430 , 4862 , . . . 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862,... 1,1,2,5,14,42,132,429,1430,4862,...
对于任意的自然数 n n n,第 n n n 个卡特兰数按下列公式定义:
C 2 n n − C 2 n n − 1 = C 2 n n n + 1 \large C_{2n}^n - C_{2n}^{n-1}= \frac{C_{2n}^n}{n+1} C2nn−C2nn−1=n+1C2nn
卡特兰数的应用场景
3.二叉树
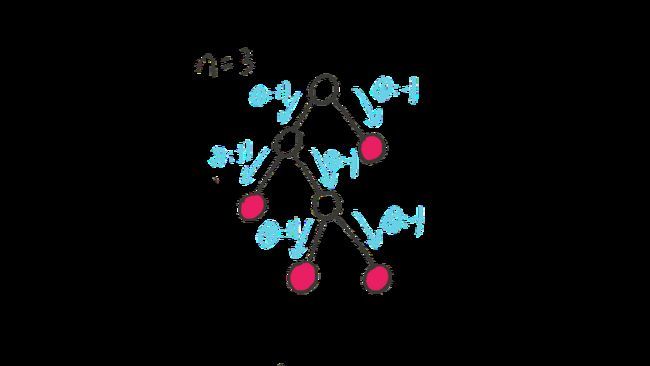
4.电影购票
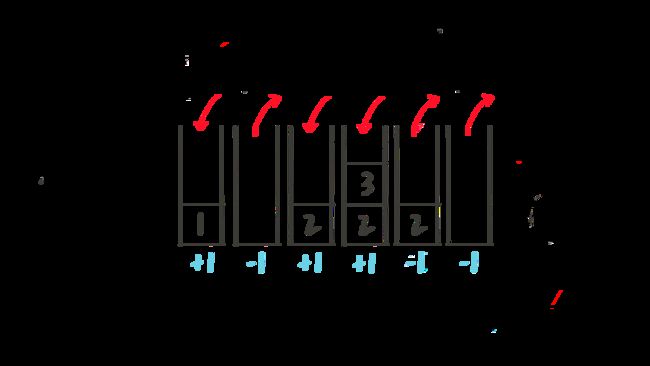
电影票一张 50 coin,且售票厅没有 coin。m 个人各自持有 50 coin,n 个人各自持有 100 coin。
则有多少种排队方式,可以让每个人都买到电影票。
满足条件的01序列
题目描述:
给定 n n n 个 0 0 0 和 n n n 个 1 1 1,它们将按照某种顺序排成长度为 2 n 2n 2n 的序列,求它们能排列成的所有序列中,能够满足任意前缀序列中 0 0 0 的个数都不少于 1 1 1 的个数的序列有多少个。
输出的答案对 1 0 9 + 7 10^9+7 109+7 取模。
输入格式:
共一行,包含整数 n n n。
输出格式:
共一行,包含一个整数,表示答案。
数据范围:
1 ≤ n ≤ 1 0 5 1≤n≤10^5 1≤n≤105
输入样例:
3
输出样例:
5
利用卡特兰数求解
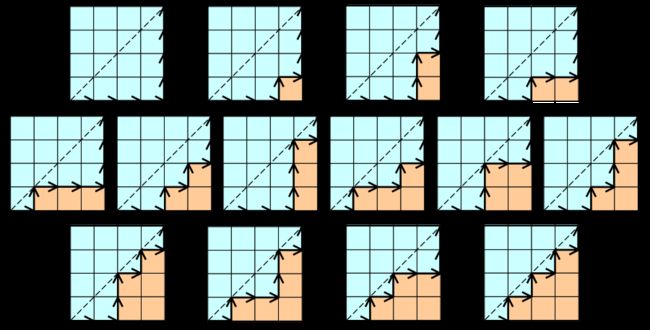
将 1 1 1 和 0 0 0 分别抽象为走网格图的竖走与横走,这样就把01序列的排列组合问题抽象为了路径排列组合问题。
因为要满足任意前缀序列中 0 0 0 的个数都不少于 1 1 1 的个数,所以 y ≤ x y \leq x y≤x,因为 x x x 与 y y y 都为正整数可进一步放缩为 y < x + 1 y < x + 1 y<x+1,所以可以抽象为在y-x坐标系上不过 y = x + 1 y = x + 1 y=x+1 直线且上从 ( 0 , 0 ) (0,0) (0,0) 到 ( 3 , 3 ) (3,3) (3,3) 的路径排列组合问题。
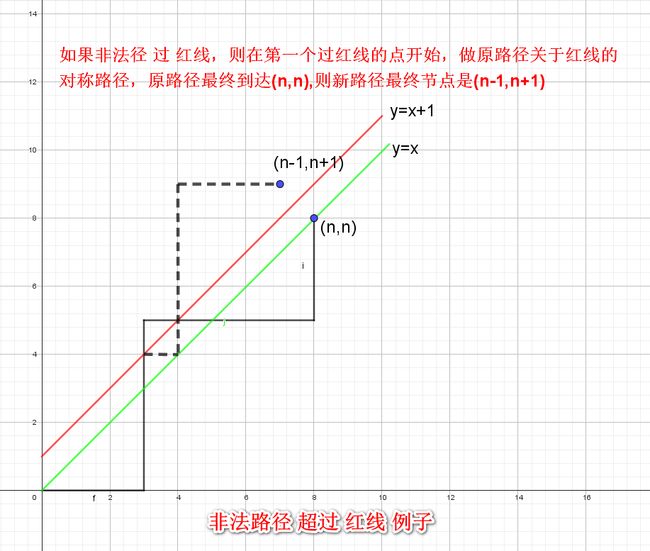
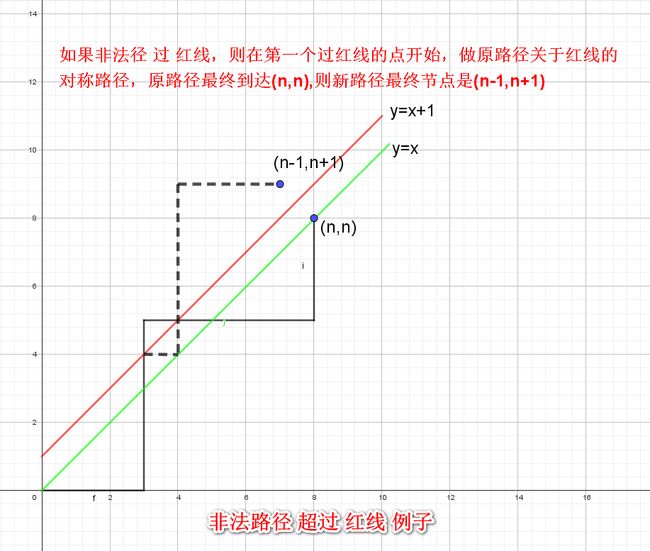
但是由于 C 6 3 C_6^3 C63 表示的是所有从 ( 0 , 0 ) (0,0) (0,0) 到 ( 3 , 3 ) (3,3) (3,3) 的路径排列组合,包括了过 y = x + 1 y = x + 1 y=x+1 直线的路径情况,因此要去除过 y = x + 1 y = x + 1 y=x+1 直线抵达终点的情况。
通过对终点 ( 3 , 3 ) (3,3) (3,3) 作出关于 y = x + 1 y = x + 1 y=x+1 直线的对称点 ( 2 , 4 ) (2,4) (2,4),所有从起点出发到达 ( 2 , 4 ) (2,4) (2,4) 的情况可看作为过 y = x + 1 y = x + 1 y=x+1 直线到终点的情况,即为 C 6 2 C_6^2 C62。因此最终结果为 C 6 3 − C 6 2 C_6^3 - C_6^2 C63−C62,根据卡特兰数可以推出结果为 C 6 3 3 + 1 \frac{C_{6}^3}{3+1} 3+1C63。
代码实现
#include