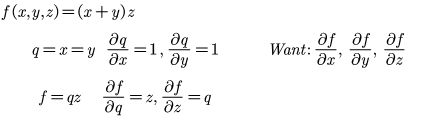普通神经网络与BP神经网络
神经网络的由来
数据的特征→决定模型的上限
模型的使用就是逼近这个上限
最典型的例子，泰坦尼克号生存数据挖掘，里面的数据已经分好类，足够干净，几乎没怎么用算法就把内在规律给挖掘了出来
数据分析中
对数据预处理，特征提取是最核心的步骤
而深度学习解决的是如何提取特征的问题
假设我们拿到一组数据
观察数据分布然后进行判断
可以进行线性切分的数据集(联想逻辑回归)
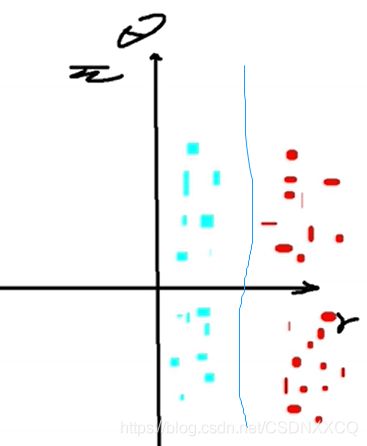
那么面对不能进行线性切分的数据分类问题(比如多分类问题还有按照圆形分布的二分类模型)，我们要怎么做呢，于是有了神经网络
神经网络缺点→无法应用到移动端，普通计算机运行太慢
神经网络基础
本质：是多个线性模型(Linear algorithm)的组合
比如，逻辑回归模型是进行二分类，相当于对数据切一刀，那么当遇到多分类或者环状分布的数据要怎么处理呢——多切几刀就行了
一， 线性函数/得分函数
在计算机视觉方面，对图片的处理就是将其转换为一个有0与1构成的矩阵，那么矩阵的形状(几乘几)就能推出像素点的大小，如假设一张猫的图片(10,10,3)大小为10* 10*3=300
假设一个对猫的识别模型公式为y=kx+b
同时我们知道，如果要对猫进行识别，那么它眼睛，鼻子在整个猫的特征中的占比/权重是不同的，那么此时我们要引入一个概念，权重参数k(一般称之为W这里为方便理解写为K)那么我们假设眼睛占比为k1，鼻子为k2，同时为了更加让计算机识别地贴近里面的眼睛，鼻子部分，我们要对该参数进行微调，眼睛为b1，鼻子为b2
那么对应的，眼睛:y=k1x+b1，鼻子:y=k2x+b2(假定只有鼻子和眼睛两个判断标准/特征)
对应的得分越高越认为它是，比如猫眼睛的得分判定为60分，对某一图片识别后，眼睛部分得分80，那么该神经网络就会认为他是猫的眼睛
计算原理：
得分(函数)=像素点值*k+b
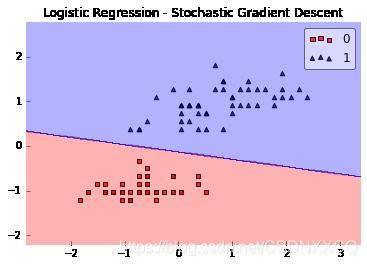
权重的更新：SGD随机梯度下降法
详见 https://blog.csdn.net/CSDNXXCQ/article/details/113527276
公式：
w = w + learning_rate * (actual_data - predict_data )
二， 损失函数
顾名思义，计算损失
目的：防止权重参数k小于0造成的得分为负
做法：改变参数k使得k能更好地正确分类
公式：
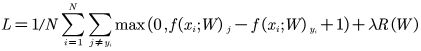
对公式的解读
Max（0，其他类别得分-正确类别得分+1），后面的加一是为了拉开不同得分之间的距离
为什么最外层是max（）：损失小于0就是没有损失
然后为了防止过拟合（比如能认出A猫的眼睛无法认出B猫的眼睛），要故意在一定程度上让预测不准(防止局部最优解问题)
特意加上正则化惩罚项λR(W),并除以N
三．Softmax分类器
目的：将上面得分函数的得分转换为概率值
公式：
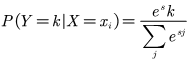→用e是为了拉开不同类型特征的距离，除以那个是为了达到归一化的目的：
计算损失值：
为什么是log：概率值→0到1之间→越接近1数值的绝对值越小
前面的负号是为了让损失函数值为正(log函数在0~1之间为负)
至此，前向传播部分结束
反向传播问题
在数据拟合的情况下，还要拟合的函数线进行微调
比如，使得算法从绿色到红色
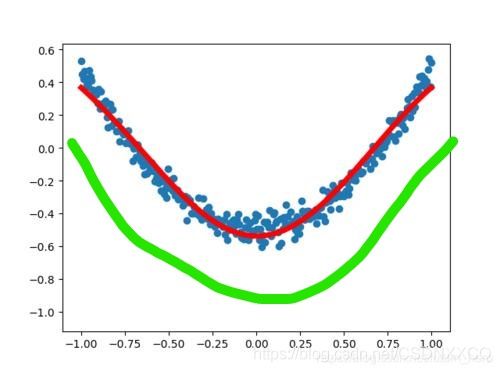
SSR(回归平方和，Regression sum of squares)与bias的引入
为了计算到底要微调到什么地步，我们要计算它与理想的拟合函数的差距，我们引入SSR，故我们要把上面的点一个个与目前的函数对应相减，得到bias(偏置值)，即bias = actual_data - preidct_data
然后对SSR求导，以期找到变化率最低的那个点，注意SSR的公式，这是个复合函数，故此时我们要使用复合函数求导，于是我们引出一个概念，链式法则
链式法则
原理:将公式的最外层一层层往里剥开，使用偏微分方程求偏导→获取变化率
是链式法则的应用
链式法则是微积分中的求导法则，用于复合函数求导。复合函数的导数将为构成复合这有限个函数在相应点的导数的乘积，称链式法则
链式法则公式：
在反向传播中的示例：
[(X*K1)K2]K3 = F(X)→[(X*K1)K2]=F(X)
公式：
在求导的过程中，复合函数的X是要不断迭代的，于是我们要引入随机梯度下降
关于随机梯度下降
参考:
https://blog.csdn.net/CSDNXXCQ/article/details/113527276
然后反复循环以上步骤，达到训练次数为止
门单元
加法门单元→平均分配
MAX门单元→选最大的
乘法门单元→互换的感觉
一般结构
圆圈即为神经元
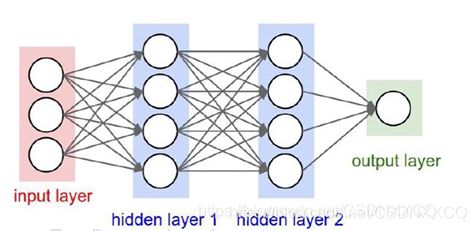
全连接层→权重参数矩阵(如输入层到隐藏层1，权重参数矩阵大小为3*4，每个神经元都为参数k1/k2之类)
图片上的英文 输入层→隐藏层1→隐藏层2→输出层，注意这里的箭头代表全连接
w即为权重参数
权重参数的更新：w0' = w0 + ndx0
其中，n为学习率，d为方向，数据在x轴上方时d为1，在下方则d为-1
通过不断的更新w使得分类趋于正确，靠近数据分类的边界
问题来了这种类似于y=kx+b的分类方法如果遇到类似于这样的数据分布(类似于圆形的分布)：
就要对坐标轴进行预处理了
使用极坐标系(polar coordinate system)
极坐标系是指在平面内由极点、极轴和极径组成的坐标系。在平面上取定一点O，称为极点。从O出发引一条射线Ox，称为极轴。再取定一个单位长度，通常规定角度取逆时针方向为正。这样，平面上任一点P的位置就可以用线段OP的长度ρ以及从Ox到OP的角度θ来确定，有序数对（ρ，θ）就称为P点的极坐标，记为P（ρ，θ）；ρ称为P点的极径，θ称为P点的极角。
坐标转化：
（1）极坐标系坐标转换为平面直角坐标系（笛卡尔坐标系）下坐标：极坐标系中的两个坐标 ρ和 θ可以由下面的公式转换为直角坐标系下的坐标值
x=ρcosθ
y=ρsinθ
（2）平面直角坐标系坐标转换为极坐标系下坐标：由上述二公式，可得到从直角坐标系中x和 y两坐标如何计算出极坐标下的坐标：
在 x= 0的情况下：若 y为正数 θ= 90° (π/2 radians)；若 y为负，则 θ= 270° (3π/2 radians).
经过极坐标处理的结果大概就是这样：
于是就达到了分类的目的
普通神经网络公式：
堆叠了一层的神经网络：
防止过拟合的手段(对抗局部最优解问题)：
手段1
正则化：即上面提到的惩罚项/惩罚系数λ(该数值越大越防止过拟合)
手段2
激活函数：
作用：进行非线性变换以期达到过拟合的目的
w→weight(权重)
bias→偏置值
a c t i v a t i o n = b i a s + ∑ i = 1 n w i ∗ x i activation = bias + \sum_{i=1}^n w_{i}*x_{i} activation=bias+i=1∑nwi∗xi
Sigmoid(逻辑回归公式):
prediction =1 if activation ≥ 0，else 0 激活即1未激活则0
但是注意，该种方法有缺陷：
他是在0~1之间的那么当结果过大的时候无法计算该数值的偏度（即梯度消失）→因为不会超过1，如果数值大于1就无法计算其偏度（变化率）
所以我们一般用relu
Relu：
要么是其本身，要么是0
手段3
Drop-out
原理：停用一部分，防止过拟合
如：第一次训练只停用神经元A，第二次训练只停用神经元B