布隆过滤器

布隆过滤器

什么是布隆过滤器

布隆过滤器 (Bloom Filter)是由 Burton Howard Bloom 于 1970 年提出，我们可以把它看作由二进制向量（或者说位数组）和一系列随机映射函数（哈希函数）两部分组成的数据结构。相比于我们平时常用的的 List、Map、Set 等数据结构，它占用空间更少并且效率更高，但是缺点是其返回的结果是概率性的，而不是非常准确的。理论情况下添加到集合中的元素越多，误报的可能性就越大。而且，存放在布隆过滤器的数据不容易删除。

Bloom Filter 会使用一个较大的 bit 数组来保存所有的数据，数组中的每个元素都只占用 1 bit ，并且每个元素只能是 0 或者 1（代表 false 或者 true），这也是 Bloom Filter 节省内存的核心所在。这样来算的话，申请一个 100w 个元素的位数组只占用 1000000Bit / 8 = 125000 Byte = 125000/1024 kb ≈ 122kb 的空间。

总结：一个名叫 Bloom 的人提出了一种来检索元素是否在给定大集合中的数据结构，这种数据结构是高效且性能很好的，但缺点是具有一定的错误识别率和删除难度。并且，理论情况下，添加到集合中的元素越多，误报的可能性就越大。

当布隆过滤器说某个值存在时，这个值可能不存在；当它说不存在时，那就肯定不存在。打个比方，当它说不认识你时，肯定就不认识；当它说见过你时，可能根本就没见过面，不过因为你的脸跟它认识的人中某脸比较相似 (某些熟脸的系数组合)，所以误判以前见过你。 套在上面的使用场景中，布隆过滤器能准确过滤掉那些已经看过的内容，那些没有看过的新内容，它也会过滤掉极小一部分 (误判)，但是绝大多数新内容它都能准确识别。这样就可以完全保证推荐给用户的内容都是无重复的。

它实际上是一个很长的二进制向量和一系列随机映射函数，二进制大家应该都清楚，存储的数据不是0就是1，默认是0。

布隆过滤器使用场景

• 网页爬虫中对URL的去重，避免爬取相同的URL地址
• 垃圾邮件过滤，从数十亿个垃圾邮件列表中判断邮箱是否是垃圾邮箱
• 秒杀系统，查看用户是否重复购买
• 数据库防止穿库。减少不存在的行或列的磁盘查找。避免代价高昂的磁盘查找会大大提高数据库查询操作的性能。
• 业务场景中判断用户是否阅读过某视频或文章，比如抖音或头条，当然会导致一定的误判，但不会让用户看到重复的内容。
• 缓存宕机、缓存击穿场景，一般判断用户是否在缓存中，如果在则直接返回结果，不在则查询db，如果来一波冷数据，会导致缓存大量击穿，造成雪崩效应，这时候可以用布隆过滤器当缓存的索引，只有在布隆过滤器中，才去查询缓存，如果没查询到，则穿透到db。如果不在布隆器中，则直接返回。
• WEB拦截器，如果相同请求则拦截，防止重复被攻击。用户第一次请求，将请求参数放入布隆过滤器中，当第二次请求时，先判断请求参数是否被布隆过滤器命中。可以提高缓存命中率。

布隆过滤器的原理

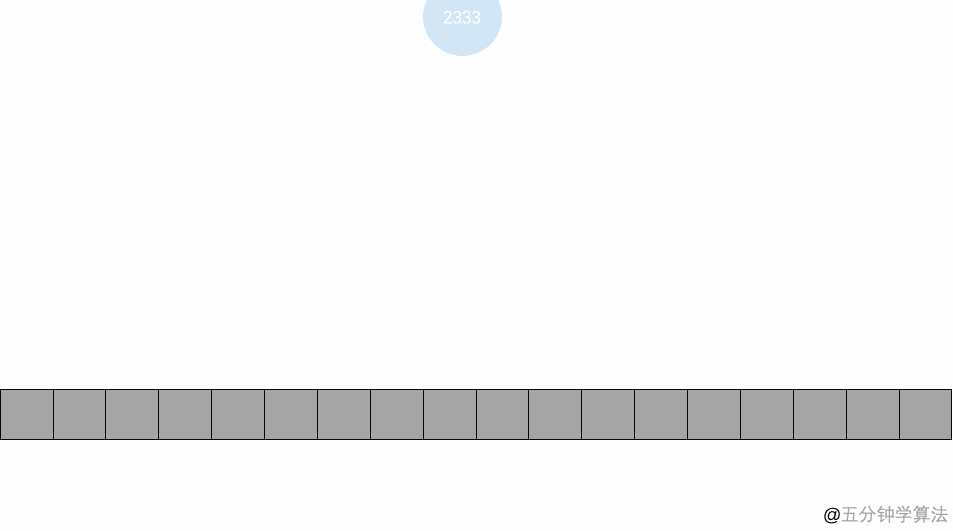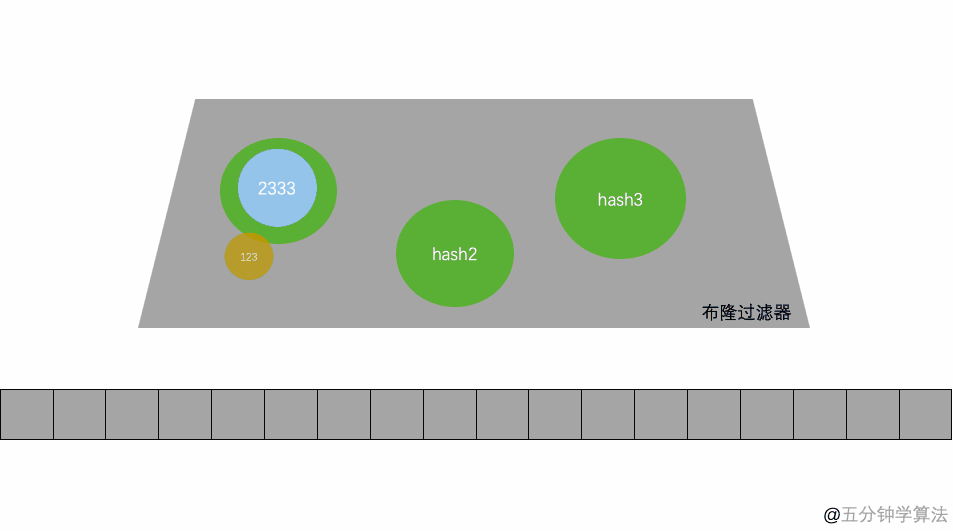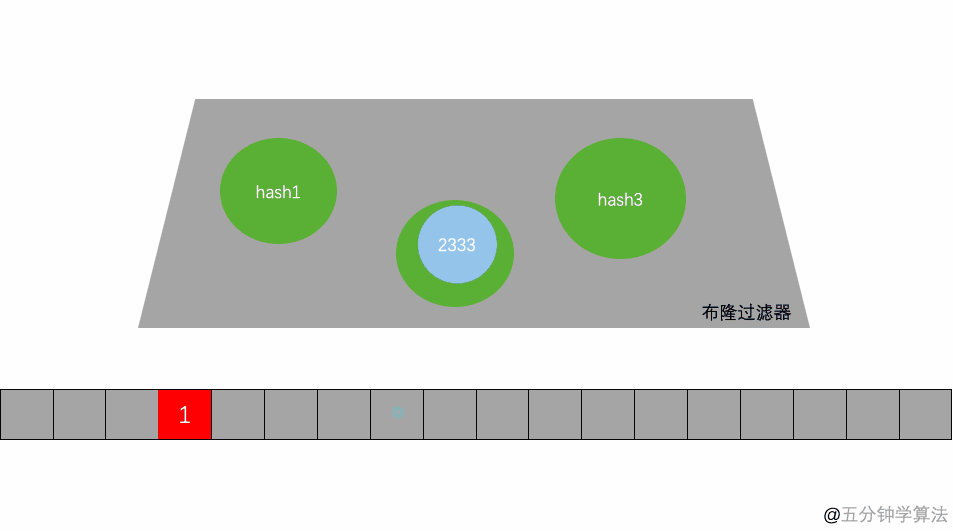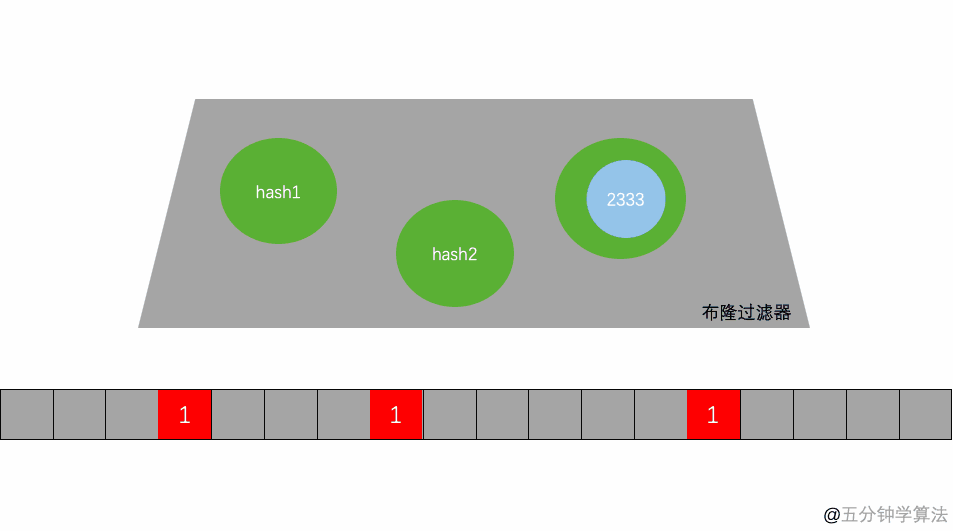
其本质就是一个只包含 0 和 1 的数组。具体操作当一个元素被加入到集合里面后，该元素通过 K 个 Hash 函数运算得到 K 个 hash 后的值，然后将 K 个值映射到这个位数组对应的位置，把对应位置的值设置为 1。查询是否存在时，我们就看对应的映射点位置如果全是 1，他就很可能存在（跟 hash 函数的个数和 hash 函数的设计有关），如果有一个位置是 0，那这个元素就一定不存在。

• 首先需要初始化一个二进制的数组，长度设为 L，同时初始值全为 0 。
• 当写入一个 A1=1000 的数据时，需要进行 H 次 hash 函数的运算 （这里为 2 次）；与 HashMap 有点类似，通过算出的 HashCode 与 L 取模后定位到 0、2 处，将该处的值设为 1。
  A2=2000 也是同理计算后将 4、7 位置设为 1。
• 当有一个 B1=1000 需要判断是否存在时，也是做两次 Hash 运算，定位到 0、2 处，此时他们的值都为 1 ，所以认为 B1=1000 存在于集合中。
• 当有一个 B2=3000 时，也是同理。第一次 Hash 定位到 index=4 时，数组中的值为 1，所以再进行第二次 Hash 运算，结果定位到 index=5 的值为 0，所以认为 B2=3000 不存在于集合中。
  整个的写入、查询的流程就是这样，汇总起来就是：

对写入的数据做 H 次 hash 运算定位到数组中的位置，同时将数据改为 1 。当有数据查询时也是同样的方式定位到数组中。一旦其中的有一位为 0 则认为数据肯定不存在于集合，否则数据可能存在于集合中。

布隆过滤器的特点

• 只要返回数据不存在，则肯定不存在。

• 返回数据存在，但只能是大概率存在。

• 同时不能清除其中的数据。

• 在有限的数组长度中存放大量的数据，即便是再完美的 Hash 算法也会有冲突，所以有可能两个完全不同的 A、B 两个数据最后定位到的位置是一模一样的。

• 删除数据也是同理，当我把 B 的数据删除时，其实也相当于是把 A 的数据删掉了，这样也会造成后续的误报。

• 基于以上的 Hash 冲突的前提，所以 Bloom Filter 有一定的误报率，这个误报率和 Hash 算法的次数 H，以及数组长度 L 都是有关的。

用于判断一个元素是否在一个集合中，0代表不存在某个数据，1代表存在某个数据。
布隆过滤器上面说了，就是一个二进制数据的集合。当一个数据加入这个集合时，经历如下洗礼

通过K个哈希函数计算该数据，返回K个计算出的hash值

这些K个hash值映射到对应的K个二进制的数组下标

将K个下标对应的二进制数据改成1。

例如，第一个哈希函数返回x，第二个第三个哈希函数返回y与z，那么：X、Y、Z对应的二进制改成1。

如图所示：

布隆过滤器的优缺点
优点

• 由于存储的是二进制数据，所以占用的空间很小

• 它的插入和查询速度是非常快的，时间复杂度是O（K），可以联想一下HashMap的过程

• 保密性很好，因为本身不存储任何原始数据，只有二进制数据

缺点

• 这就要回到我们上面所说的那些缺点了。

• 添加数据是通过计算数据的hash值，那么很有可能存在这种情况：两个不同的数据计算得到相同的hash值。
  

例如图中的“你好”和“hello”，假如最终算出hash值相同，那么他们会将同一个下标的二进制数据改为1。

这个时候，你就不知道下标为2的二进制，到底是代表“你好”还是“hello”。

由此得出如下缺点：

一、存在误判
假如上面的图没有存"hello"，只存了"你好"，那么用"hello"来查询的时候，会判断"hello"存在集合中。

因为“你好”和“hello”的hash值是相同的，通过相同的hash值，找到的二进制数据也是一样的，都是1。

二、删除困难

还是用上面的举例，因为“你好”和“hello”的hash值相同，对应的数组下标也是一样的。

这时候想去删除“你好”，将下标为2里的二进制数据，由1改成了0。

那么我们是不是连“hello”都一起删了呀。（0代表有这个数据，1代表没有这个数据）

代码实现

依赖

<dependency>
    <groupId>com.google.guavagroupId>
     <artifactId>guavaartifactId>
     <version>19.0version>
 dependency>

代码实现

import com.google.common.hash.BloomFilter;
import com.google.common.hash.Funnels;

public class BloomFilterDemo {
    /**
     * 预计要插入多少数据
     */
    private static int size = 1000000;

    /**
     * 期望的误判率
     */
    private static double fpp = 0.01;

    /**
     * 布隆过滤器
     */
    private static BloomFilter<Integer> bloomFilter = BloomFilter.create(Funnels.integerFunnel(), size, fpp);


    public static void main(String[] args) {
        // 插入10万样本数据
        for (int i = 0; i < size; i++) {
            bloomFilter.put(i);
        }

        // 用另外十万测试数据，测试误判率
        int count = 0;
        for (int i = size; i < size + 100000; i++) {
            if (bloomFilter.mightContain(i)) {
                count++;
                System.out.println(i + "误判了");
            }
        }
        System.out.println("总共的误判数:" + count);
    }
}

参考资料：
https://blog.csdn.net/AmazDreamer/article/details/131318054
https://my.oschina.net/jiagoushi/blog/8596752
IT老哥