聚类方法简单总结
聚类概述
聚类(cluster)与分类(class)问题不同,聚类属于无监督学习模型,而分类属于有监督学习模型。聚类使用某种算法将样本分为N个群落,群落内部相似度较高,群落之间相似度较低。通常采用‘距离’来度量样本间的相似度,距离越小,相似度越高;距离越大,相似度越低。
相似度度量方式
- 欧氏距离
∣ x 1 − x 2 ∣ = ( x 1 − x 2 ) 2 |x_1 - x_2| = \sqrt{(x_1 - x_2)^2} ∣x1−x2∣=(x1−x2)2 - 曼哈顿距离
二维平面两点 a ( x 1 , y 1 ) 与 b ( x 2 , y 2 ) a(x_1, y_1)与b(x_2, y_2) a(x1,y1)与b(x2,y2)两点间的曼哈顿距离为:
d ( a , b ) = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ d(a, b) = |x_1 - x_2| + |y_1 - y_2| d(a,b)=∣x1−x2∣+∣y1−y2∣
将其扩展到N维空间, a ( x 1 , x 2 , . . . , x n ) a(x_1, x_2,... , x_n) a(x1,x2,...,xn)与 b ( y 1 , y 2 , . . . , y n ) b(y_1, y_2,... , y_n) b(y1,y2,...,yn)之间的曼哈顿距离为:
d ( a , b ) = ∣ x 1 − y 1 ∣ + ∣ x 2 − y 2 ∣ + . . . + ∣ x n − y n ∣ = ∑ i = 1 n ∣ x i − y i ∣ d(a,b) = |x_1-y_1| + |x_2-y_2| + ... + |x_n-y_n| = \sum_{i=1}^{n}|x_i - y_i| d(a,b)=∣x1−y1∣+∣x2−y2∣+...+∣xn−yn∣=i=1∑n∣xi−yi∣

上图中,绿色线条表示为欧氏距离,红色表示曼哈顿距离,黄色和蓝色线条表示的为曼哈顿距离的等价长度。 - 闵可夫斯基距离
闵可夫斯基距离(Minkowski distance) 又称闵氏距离:
D ( x , y ) = ( ∑ i = 1 n ∣ x i − y i ∣ p ) 1 p D(x,y) = (\sum_{i=1}^{n}|x_i - y_i|^p)^\frac{1}{p} D(x,y)=(i=1∑n∣xi−yi∣p)p1- p=1时,D为曼哈顿距离
- p=2时,D为欧式距离
- p → ∞ \rightarrow \infty →∞时,D为切比雪夫距离。
因此,曼哈顿距离、欧氏距离都是闵可夫斯基距离的特殊形式。
- 距离性质
如果dist(x,y)度量标准为一个距离,则满足: - 非负性:dist(x,y) >= 0;
- 同一性:dist(x,y) = 0时,x=y;
- 对称性:dist(x,y) = dist(y,x);
- 直递性:dist(x,y) <= dist(x,z) + dist(z,y)
聚类算法划分
- 原型聚类
原型聚类亦称“基于原型的聚类”(prototype-based clustering),此类算法假设聚类问题可以通过一组原型表示。一般,算法先对原型进行初始化,然后对原型进行迭代更新求解。采用不同的原型表示,将有不同的求解方式,对应不同的算法。最著名的算法就包括:K-Means。 - 密度聚类
密度聚类亦称“基于密度的聚类”(density-based clustering),此类算法假定聚类结构能够通过样本分布的紧密程度确定。一般,密度聚类算法从样本密度的角度考虑样本之间的连接性,并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。比较著名的密度聚类算法有DBSCAN。 - 层次聚类
层次聚类(hierarchical clustering)试图在不同层次对数据集进行划分,从而形成树形的聚类结果。数据集的划分可以采用“自底向上”或者“自顶向下”的策略。常用的层次聚类算法包括凝聚层次算法等。
常用聚类算法
1)k均值聚类(K-Means clustering)算法是一种常用的、基于原型的聚类算法。执行步骤为:
- 根据事先确定的聚类数,随机选择若干样本作为聚类中心,计算每个样本与每个聚类中心的欧式距离,离哪个聚类中心最近,就算哪个聚类中心的聚类簇,所有点有归属之后则一次聚类完成;
- 然后再计算每个聚类的集合中心,如果几何中心与前一次的聚类中心不重合,就再次以新的几何中心作为新的聚类中心,重新划分聚类。
- 重复以上过程,直至完成聚类后,各个聚类簇的中心与其所依据的聚类中心重合或者小于设定的阈值,表明聚类任务完成。

注意:
1)聚类数目(K)必须事先确定;
2)最终的聚类结果会因初始中心的选择不同而异,并且模型容易受到噪声点的干扰
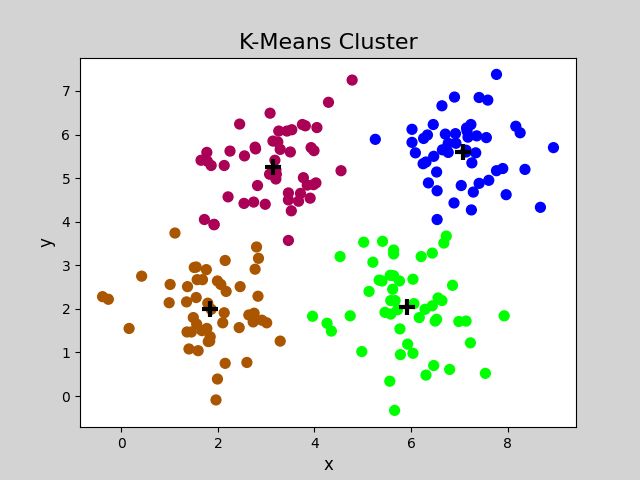
K-Means简单演示
import numpy as np
import sklearn.cluster as sc
import sklearn.metrics as sm
import matplotlib.pyplot as plt
x = []
with open("D:/python/data/multiple3.txt", 'r') as f:
for line in f.readlines():
data = [float(substr) for substr in line.split(',')]
x.append(data)
x = np.array(x)
print(x.shape)
# k均值聚类器
model = sc.KMeans(n_clusters=4) # n_clusters为事先预定的聚类簇数量
# 训练
model.fit(x)
cluster_labels_ = model.labels_ # 每一个点的聚类结果
cluster_centers_ = model.cluster_centers_ # 获得聚类几何中心
print('cluster_labels_: ', cluster_labels_)
print('cluster_centers_: ', cluster_centers_)
silhouette_score = sm.silhouette_score(x, cluster_labels_,
sample_size=len(x),
metric='euclidean' # 欧式距离度量方式
)
print('silhouette_score: ', silhouette_score)
print('--------可视化--------')
plt.figure('K-Means Cluster', facecolor='lightgray')
plt.title('K-Means Cluster', fontsize=16)
plt.xlabel('x', fontsize=12)
plt.ylabel('y', fontsize=12)
plt.tick_params(labelsize=10)
plt.scatter(x[:,0], x[:,1], s=50, c=cluster_labels_, cmap='brg')
plt.scatter(cluster_centers_[:,0], cluster_centers_[:,1], marker='+',
c='black', s=120, linewidths=3)
plt.show()
"""
cluster_labels_: [2 2 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 1 1 3 0 2 1 3 0 2 1 3 0 2
1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1
3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 3 1 3 0 2 1 3 0 2 1 3 0 2 1 3
0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0
2 2 3 0 2 1 3 0 2 1 3 1 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2
1 3 0 2 1 3 0 2 1 3 0 2 1 3 0]
cluster_centers_: [[7.07326531 5.61061224]
[3.1428 5.2616 ]
[1.831 1.9998 ]
[5.91196078 2.04980392]]
silhouette_score: 0.5773232071896658
"""
特点
- 优点
- 原理简单,实现方便,收敛速度较快;
- 聚类效果较好,模型可解释性强
- 缺点
- 需要事先预定聚类簇数量;
- 初始中心选择对聚类效果有影响,可能得到局部最优解;
- 对噪声敏感
- 使用条件
- 事先可以知道聚类数量
- 数据分布具有明显的中心
2)噪声聚类DBSCAN(Density-Based Spatial Clustering of Applications with Noise)。执行步骤为:
- 随机选择一个样本作为圆心,以事先确定的半径画圆,凡是圈中的样本点都被划分到与圆心样本同一个聚类,然后再以这些被圈中的样本点为圆心,以事先确定的半径画圆,不断加入新的样本,扩大聚类的规模,直至不再有新的样本加入,即完成一个聚类;
- 重复以上的步骤直至所有的样本点划分完毕。

DBSCAN中,样本点分为三类: - 边界点:不能发展出新的样本点,但是属于一个聚类;
- 噪声点:无法划分到某类中的点;
- 核心点:除了边界点和噪声点都是核心点,其可以发展出新的样本点。
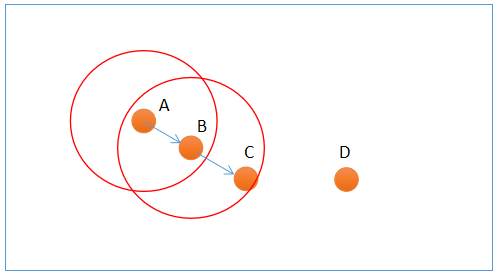
其中,样本点A、B属于可以发展出新的样本点的核心点,C是不可以发展出新的样本点的边界点;D由于无法划分到任何类别而被视为噪声点。
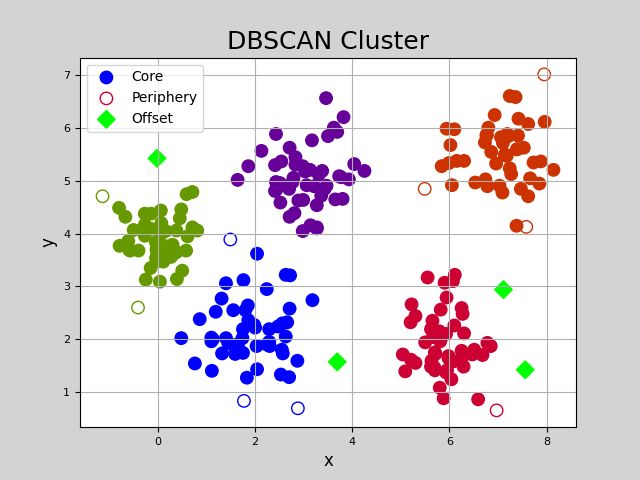
DBSCAN简单演示
import numpy as np
import sklearn.cluster as sc
import matplotlib.pyplot as plt
import sklearn.metrics as sm
x = []
with open('D:/python/data/perf.txt', 'r') as f:
for line in f.readlines():
data = [float(substr) for substr in line.split(',')]
x.append(data)
x = np.array(x)
print(x.shape)
# 模型超参数
radius = 0.8 # 邻域半径
min_samples = 5 # 聚类簇最少样本点数量
# 创建噪声密度聚类器
model = sc.DBSCAN(eps=radius, min_samples=min_samples)
# 训练模型
model.fit(x)
# 划分结果
cluster_labels_ = model.labels_
# 评价聚类模型
score = sm.silhouette_score(x, model.labels_,
sample_size=len(x),
metric='euclidean') # 轮廓系数
print('silhouette_score: ', score)
# silhouette_score: 0.6366395861050828
# 区分三类样本
# 核心样本
core_mask = np.zeros(len(x), dtype=bool)
core_mask[model.core_sample_indices_] = True
# 噪声样本
offset_mask = cluster_labels_==-1
# 边界样本
border_mask = ~(core_mask | offset_mask)
print('--------可视化--------')
plt.figure('DBSCAN Cluster', facecolor='lightgray')
plt.title('DBSCAN Cluster', fontsize=18)
plt.xlabel('x', fontsize=12)
plt.ylabel('y', fontsize=12)
plt.tick_params(labelsize=8)
plt.grid(':')
labels = set(cluster_labels_)
cs = plt.get_cmap('brg', len(labels))(range(len(labels)))
# 核心点
plt.scatter(x[core_mask][:, 0],
x[core_mask][:, 1],
c=cs[cluster_labels_[core_mask]],
s=80, label='Core')
# 边界点
plt.scatter(x[border_mask][:, 0],
x[border_mask][:, 1],
edgecolor=cs[cluster_labels_[border_mask]],
facecolor='none', s=80, label='Periphery')
# 噪声点
plt.scatter(x[offset_mask][:, 0],
x[offset_mask][:, 1],
marker='D', c=cs[cluster_labels_[offset_mask]],
s=80, label='Offset')
plt.legend()
plt.show().
特点
- 优点
- 不需要提前确定聚类簇数量;
- 能够有效处理噪声点(因为当一个聚类簇的样本点数量少于阈值时会被当作噪声点处理);
- 可以处理任何形状的空间聚类。
- 缺点
- 当数据量过大时,要求较大的内存支持I/O消耗很大;
- 当空间聚类的密度不均匀时、聚类间距差别很大时,聚类效果有偏差;
- 邻域半径和最少样本数量两个参数对聚类结果影响最大。
- 何时选择噪声密度
- 数据稠密、没有明显聚类中心;
- 噪声数据较多;
- 未知聚簇的数量
3)凝聚层次(Agglomerative)算法,执行步骤为:
首先将每个样本看作独立的聚类,如果聚类数大于预设的数值,则合并最近的样本作为一个新的聚类,如此反复迭代,不断扩大聚类规模的同时减少聚类的总数。直到聚类减少到预设数值为止。凝聚层次算法的核心是如何衡量不同的聚类簇之间的距离。
- 以距离将凝聚层次算法分为
- ward:默认选项,使用方差作为标准,假设簇A、簇B合并后使得所有簇的方差增加最小,则选择合并A、B;
- average:将两个簇中所有点之间平均距离最小的两个簇合并;
- complete:将两个簇中点的最大距离最小的两个簇合并
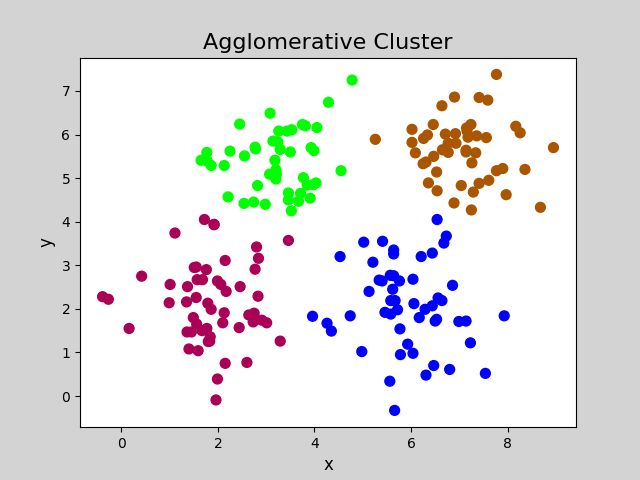
凝聚层次简单实现
import numpy as np
import sklearn.cluster as sc
import sklearn.metrics as sm
import matplotlib.pyplot as plt
x = []
with open("D:/python/data/multiple3.txt", 'r') as f:
for line in f.readlines():
data = [float(substr) for substr in line.split(',')]
x.append(data)
x = np.array(x)
print(x.shape)
# 凝聚层次聚类器
model = sc.AgglomerativeClustering(n_clusters=4) # n_clusters为事先预定的聚类簇数量
# 训练
model.fit(x)
# 获取预测结果
cluster_labels_ = model.labels_ # 每一个点的聚类结果
silhouette_score = sm.silhouette_score(x, cluster_labels_,
sample_size=len(x),
metric='euclidean' # 欧式距离度量方式
)
print('silhouette_score: ', silhouette_score)
# silhouette_score: 0.5736608796903743
print('--------可视化--------')
plt.figure('Agglomerative Cluster', facecolor='lightgray')
plt.title('Agglomerative Cluster', fontsize=16)
plt.xlabel('x', fontsize=12)
plt.ylabel('y', fontsize=12)
plt.tick_params(labelsize=10)
plt.scatter(x[:,0], x[:,1], s=50, c=cluster_labels_, cmap='brg')
plt.show()
特点
- 需要事先确定分类簇数量(K);
- 不依赖于中心点的划分,所以对于中心特征不明显的样本,划分效果更佳稳定;
聚类问题之评价指标
理想的聚类问题可以概括为:内密外疏,即同一聚类内部足够紧密,聚类之间足够疏远。学科中使用“轮廓系数”进行度量,见下图:

假设已经通过某算法,将样本点进行聚类,对于簇中每个样本,分别计算出轮廓系数。对于其中某个聚类簇而言:
a(i) = average(i向量到所有它属于的簇中其他点的距离)
b(i) = min(i向量到其他簇内所有点的平均距离)
则i向量的轮廓系数为:
S ( i ) = b ( i ) − a ( i ) m a x ( a ( i ) , b ( i ) ) S(i) = \frac{b(i) - a(i)}{max(a(i), b(i))} S(i)=max(a(i),b(i))b(i)−a(i)
由公式可知:
- b(i) >> a(i)时,S(i) → 1 \rightarrow 1 →1,聚类效果最好;
- b(i) << a(i)时,S(i) → − 1 \rightarrow -1 →−1,聚类效果最差;
- b(i) == a(i)时,S(i) = 0,分类出现重叠。
sklearn中提供的轮廓系数API:
score = sm.silhouette_score(x, # 样本
clustering_labels_, # 标签
sample_size=len(x), # 样本数量
metric="euclidean") # 欧式距离度量
OK,简单总结就是如此。真的希望可以结识更多志同道合的朋友,一起加油,未来真的是如此精彩。。。