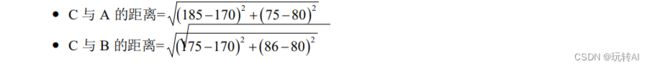opencv 进阶04-搞懂什么是 K邻近算法
机器学习算法是从数据中产生模型,也就是进行学习的算法(下文也简称为算法)。我们把经验提供给算法,它就能够根据经验数据产生模型。在面对新的情况时,模型就会为我们提供判断(预测)结果。例如,我们根据“个子高、腿长、体重轻”判断一个孩子是个运动员的好苗子。把这些数据量化后交给计算机,它就会据此产生模型,在面对新情况时(判断另一个孩子能不能成为运动员),模型就会给出相应的判断。
数据特征
比如,要对一组孩子进行测试,首先就要获取这组孩子的基本数据。这组数据包含 身高、腿长、体重等数据,这些反映对象(也可以是事件)在某个方面的表现或者性质的事项,被称为属性或特征。而具体的值,如反映身高的“188 cm”就是特征值或属性值。这组数据的集合“(身高=188 cm,腿长=56 cm,体重=46 kg),……,(身高=189 cm,腿长=55 cm,体重=48 kg)”,称为数据集,其中每个孩子的数据称为一个样本。
从数据中学得模型的过程称为学习(learning)或者训练(training)。在训练过程中所使用的数据称为训练数据,其中的每个样本称为训练样本,训练样本所组成的集合称为训练集。
当然,如果希望获取一个模型,除了有数据,还需要给样本贴上对应的标签(label)。例如,“((个子高、腿长、体重轻),好苗子)”。这里的“好苗子”就是标签,通常我们将拥有了标签的样本称为“样例”。
学得模型后,为了测试模型的效果,还要对其进行测试,被测试的样本称为测试样本。输入测试样本时,并不提供测试样本的标签(目标类别),而是由模型决定样本的标签(属于哪个类别)。比较测试样本预测的标签与实际样本标签之间的差别,就可以计算出模型的精确度。
大多数的机器学习算法都来源于日常生活实践。K 近邻算法是最简单的机器学习算法之一,主要用于将对象划分到已知类中,在生活中被广泛使用。例如,教练要选拔一批长跑运动员,如何选拔呢?他使用的可能就是 K 近邻算法,会选择个子高、腿长、体重轻,膝、踝关节围度
小,跟腱明显,足弓较大者作为候选人。他会觉得这样的孩子有运动员的潜质,或者说这些孩子的特征和运动员的特征很接近。
K 近邻算法的基本思想
K 近邻算法的本质是将指定对象根据已知特征值分类。例如,看到一对父子,一般情况下,通过判断他们的年龄,能够马上分辨出哪位是父亲,哪位是儿子。这是通过年龄属性的特征值来划分的。
上述例子是最简单的根据单个特征维度做的分类,在实际场景中,情况可能更复杂,有多个特征维度。例如,为一段运动视频分类,判断这段视频是乒乓球比赛还是足球比赛。
为了确定分类,需要定义特征。这里定义两个特征,一个是运动员“挥手”的动作,另一个是运动员“踢脚”的动作。当然,我们不能一看到“挥手”动作就将视频归类为“乒乓球比赛”,因为我们知道某些足球运动员习惯在运动场上通过挥手来跟队友进行交流。同样,我们也不能一看到“踢脚”动作就将视频归类为“足球比赛”,因为有些乒乓球运动员会通过“踢脚”动作来表达自己的感情。
我们分别统计在某段特定时间内,视频中“挥手”和“踢脚”动作的次数,发现如下规律:
- 在乒乓球比赛的视频中,“挥手”的次数远多于“踢脚”的次数。
- 在足球比赛的视频中,“踢脚”的次数远多于“挥手”的次数。
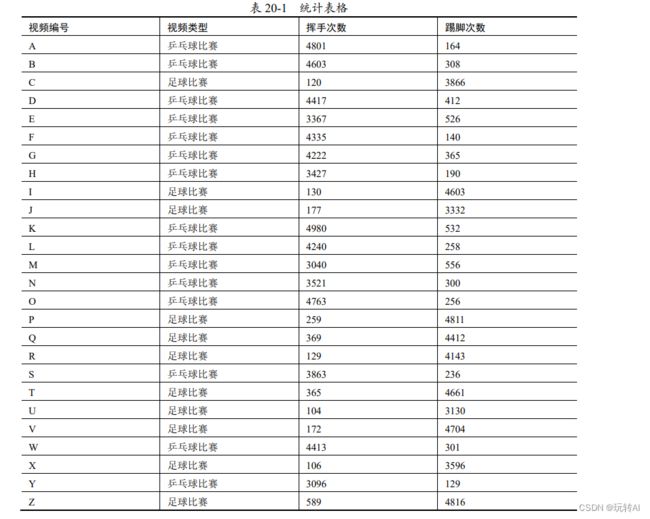
根据对一组视频的分析,得到如表 20-1 所示的数据。
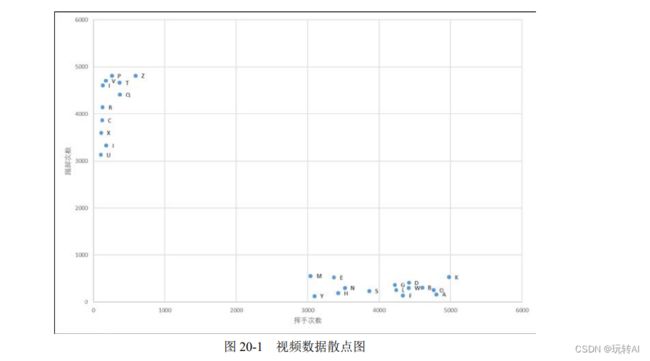
为了方便观察,将上述数据绘制为散点图,如图 20-1 所示。
从图 20-1 中可以看到,数据点呈现聚集特征:
- 乒乓球比赛视频中的数据点聚集在 x 轴坐标为[3000, 5000],y 轴坐标为[1,500]的区域。
- 足球比赛视频中的数据点聚集在 y 轴坐标为[3000, 5000],x 轴坐标为[1,500]的区域。
此时,有一个视频 Test,经过统计得知其中出现 2000 次“挥手”动作,100 次“踢脚”动作。如果在图 20-1 中标注其位置,可以发现视频 Test 的位置最近的邻居是乒乓球比赛视频,因此可判断该视频是乒乓球比赛视频。
上面的例子是一个比较极端的例子,非黑即白,而实际的分类数据中往往参数非常多,判断起来也不会如此简单。因此,为了提高算法的可靠性,在实施时会取
k 个近邻点,这 k 个点中属于哪一类的较多,然后将当前待识别点划分为哪一类。为了方便判断,k
值通常取奇数,这和为了能得到明确的投票结果通常将董事会成员安排为奇数的道理是一样的。
例如,已知某知名双胞胎艺人 A 和 B 长得很像,如果要判断一张图像 T 上的人物到底是艺人 A 还是艺人 B,则采用 K 近邻算法实现的具体步骤如下:
(1)收集艺人 A 和艺人 B 的照片各 100 张。
(2)确定几个用来识别人物的重要特征,并使用这些特征来标注艺人 A 和 B 的照片。
例如,根据某 4 个特征,每张照片可以表示为[156, 34, 890, 457]这样的形式(即一个样本点)。按照上述方式,获得艺人 A 的
100 张照片的数据集 FA,艺人 B 的 100 张照片的数据集 FB。此时数据集 FA、FB
中的元素都是上述特征值的形式,每个集合中各有 100 个这样的特征值。简而言之,就是使用数值来表示照片,得到艺人 A
的数值特征集(数据集)FA、艺人 B 的数值特征集 FB。
(3)计算待识别图像 T 的特征,并使用特征值表示图像 T。例如,图像 T 的特征值 TF 可
能为[257, 896, 236, 639]。
(4)计算图像 T 的特征值 TF 与 FA、FB 中各特征值之间的距离。
(5)找出产生其中 k 个最短距离的样本点(找出离 T 最近的 k 个邻居),统计 k 个样本点中属于 FA 和 FB 的样本点个数,属于哪个数据集的样本点多,就将 T 确定为哪个艺人的图像。
例如,找到 11 个最近的点,在这 11 个点中,属于 FA 的样本点有 7 个,属于 FB 的样本点有 4个,那么就确定这张图像 T 上的艺人为 A;反之,如果这 11 个点中,有 6 个样本点属于 FB,有 5 个样本点属于 FA,那么就确定这张图像 T 上的艺人为 B。
以上所述就是 K 近邻算法的基本思想。
计算思想
计算机的“感觉”是通过逻辑计算和数值计算来实现的。所以,在大多数的情况下,我们要对计算机要处理的对象进行数值化处理,将其量化为具体的值,以便后续处理。
K 近邻算法在获取各个样本的特征值之后,计算待识别样本的特征值与各个已知分类的样本特征值之间的距离,然后找出 k 个最邻近的样本,根据 k 个最邻近样本中占比最高的样本所属的分类,来确定待识别样本的分类。
01.归一化
对于简单的情况,直接计算与特征值的距离(差距)即可。
例如,在某影视剧中,已经通过技术手段获知犯罪嫌疑人的身高为 186 cm,受害人身高为 172 cm。而面对警察,甲、乙二人都宣称自己是受害人。
此时,我们可以通过测量二人身高判定谁是真正的受害人:
- 甲身高为 185 cm,与嫌疑人身高的距离=186-185=1cm,与受害人身高的距离=185-172=7cm。甲的身高与嫌疑人更接近,因此确认甲为嫌疑人。
- 乙身高为 173 cm,与嫌疑人身高的距离=186-173=13cm,与受害人身高的距离=173-172=1cm。乙的身高与受害人更接近,因此确认乙为受害人。
上面的例子是非常简单的特例。而在实际场景中,可能需要通过更多参数进行判断。
例如,在一部国外影视剧中,警察通过技术手段获知嫌疑人的身高为 180 cm,缺一根手指;受害人身高为 173cm,十指健全。此时,前来投案的甲、乙二人都宣称自己是受害人。
当有多个参数时,一般将这些参数构成列表(数组)进行综合判断。本例以(身高,手指数量)作为特征。
因此,嫌疑人的特征值为(180, 9),受害人的特征值为(173, 10)。
此时,可以对二人进行以下判断:
- 甲身高为 175 cm,缺一根手指,甲的特征值为(175, 9)。
- 甲与嫌疑人特征值的距离 = (180-175) + (9-9) = 5
- 甲与受害人特征值的距离 = (175-173) + (10-9) = 3
此时,甲的特征值与受害人更接近,断定甲为受害人
- 乙身高为 178 cm,十指健全,乙的特征值为(178, 10)。
- 乙与嫌疑人特征值的距离 = (180-178) + (10-9) = 3
- 乙与受害人特征值的距离 = (178-173) + (10-10) = 5
此时,乙与嫌疑人的特征值更接近,断定乙为嫌疑人。
当然,我们知道上述结果是错误的。因为身高、手指数量有着不同的量纲(权值),所以在计算与特征值的距离时要充分考虑不同参数之间的权值。通常情况下,由于各个参数的量纲不一致等原因,需要对参数进行处理,让所有参数具有相等的权值。
一般情况下,对参数进行归一化处理即可。做归一化时,通常使用特征值除以所有特征值中的最大值(或者最大值与最小值的差)。
例如,上例中用身高除以最高身高 180(cm),每个人手指数量 除以 最多手指数10(10 根手指),得到新的特征值,计算方式为:
归一化特征 =(每人身高/最高身高 180,手指数量/做多手指数10)
因此,经过归一化以后:
- 嫌疑人的特征值为(180/180, 9/10) = (1, 0.9)
- 受害人的特征值为(173/180, 10/10) = (0.96, 1)
此时,可以根据归一化以后的特征值,对二人进行判断:
- 甲的特征值为(175/180, 9/10)=(0.97, 0.9)
- 甲与嫌疑人特征值的距离= (1-0.97) + (0.9-0.9) = 0.03
- 甲与受害人特征值的距离= (0.97-0.96) + (1-0.9) = 0.11
此时,甲与犯罪嫌疑人的特征值更接近,断定甲为犯罪嫌疑人。
-
乙的特征值为(178/180, 10/10)=(0.99, 1)
-
乙与嫌疑人的特征值距离= (1-0.99) + (1-0.9) = 0.11
-
乙与受害人的特征值距离= (0.99-0.96) + (1-1) = 0.03
此时,乙与受害人的特征值更接近,断定乙为受害人。
02.距离计算
在前面的讨论中,我们多次计算了距离。使用的方式是先将特征值中对应的元素相减,然后再求和。
例如,有(身高,体重)形式的特征值 A(185, 75)和 B(175, 86),下面判断 C(170, 80)与特征值 A 和特征值 B 的距离:
- C 与 A 的距离= (185-170) + (75-80) = 15+(-5) =10
- C 与 B 的距离= (175-170) + (86-80) = 5+6 = 11
通过计算,C 与 A 的距离更近,所以将 C 划归为 A 所属的分类。
当然,我们知道上述判断是错误的,因为在计算 C 与 A 的距离时存在负数,它抵消了一部分正数。所以,为了避免这种正负相抵的情况,我们通常会计算绝对值的和:
- C 与 A 的距离= |185-170|+|75-80| = 15+5 = 20
- C 与 B 的距离= |175-170|+|86-80| = 5+6 = 11
取绝对值后再求和,计算出 C 与 B 的距离更近,将 C 归为 B 所属的分类。这种用绝对值之和表示的距离,称为
曼哈顿距离。
像这样计算距离已经基本满足要求了,但是还有更好的方法。例如,可以引入计算平方和的方式。此时的计算方法是:
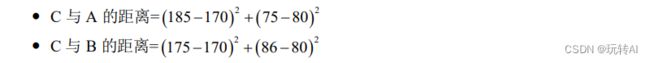
更普遍的形式是计算平方和的平方根,这种距离就是被广泛使用的欧氏距离,它的计算方法是:
看完后尝试用自己的理解白话一下K邻近算法,评论区见!!!