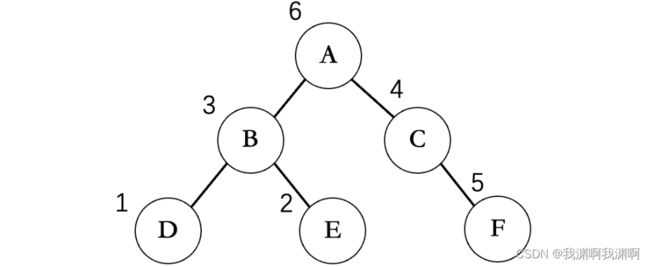
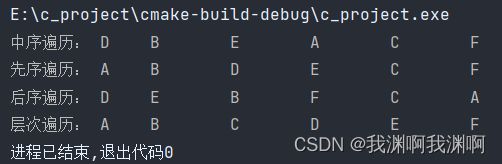
数据结构-树

1. 二叉树遍历

#include 
#include "stdio.h"
#include "stdlib.h"

typedef struct TNode *Position;
typedef Position BinTree; // 二叉树类型
typedef char ElementType;


// 树结点定义
struct TNode {
    ElementType Data; // 结点数据
    BinTree Left; // 指向左子树
    BinTree Right; // 指向右子树
};

// 中序遍历 左->中->右
void InorderTraversal(BinTree BT) {
    if (BT) {
        InorderTraversal(BT->Left);
        printf("%c\t", BT->Data);
        InorderTraversal(BT->Right);
    }
}

// 先序遍历 中->左->右
void PreorderTraversal(BinTree BT) {
    if (BT) {
        printf("%c\t", BT->Data);
        PreorderTraversal(BT->Left);
        PreorderTraversal(BT->Right);
    }
}

// 后序遍历 左->右->中
void PostorderTraversal(BinTree BT) {
    if (BT) {
        PostorderTraversal(BT->Left);
        PostorderTraversal(BT->Right);
        printf("%c\t", BT->Data);
    }
}

// 定义队列中结点
struct QueueNode {
    BinTree Data;
    struct QueueNode * Next;
};
typedef struct QueueNode * QNode;
// 定义队列
struct Queue{
    QNode Front, Rear; // 队列头尾指针
};
typedef struct Queue *LinkedQueue;

bool IsEmpty(LinkedQueue Q){
    return (Q->Front == Q->Rear);
}

bool CreatQueue(LinkedQueue Q){
    QNode node = malloc(sizeof(struct QueueNode));
    if(node == NULL) return 0;

    Q->Front = Q->Rear = node;
    return true;
}

bool AddQueue(LinkedQueue Q,BinTree X){
    QNode newNode = malloc(sizeof (struct QueueNode));
    newNode->Data = X;
    Q->Rear->Next = newNode;
    Q->Rear = newNode;
    return true;
}

BinTree DeleteQueue(LinkedQueue Q){

    BinTree e = Q->Front->Next->Data;
    QNode node = Q->Front->Next;
    if(Q->Front==Q->Rear) Q->Front=Q->Rear=NULL;
    Q->Front->Next = Q->Front->Next->Next;
    if(Q->Rear == node) Q->Rear = Q->Front;
    free(node);
    return e;
}


// 层次遍历 从上到下，从左到右
void LevelorderTraversal(BinTree BT) {
    LinkedQueue queue;   //先搞一个队列
    queue = malloc(sizeof (struct Queue));
    BinTree node;

    if(!BT) return;

    CreatQueue(queue);
    AddQueue(queue,BT);

//    printf("run");
    while (IsEmpty(queue)==0) {   //不断重复，直到队列空为止
        node = DeleteQueue(queue);   //出队一个元素，打印值

        printf("%c\t", node->Data);
        if(node->Left)    //如果存在左右孩子的话
            AddQueue(queue, node->Left);
        if(node->Right)
            AddQueue(queue, node->Right);
    }

}

int main() {
    BinTree A = malloc(sizeof(struct TNode));
    A->Data = 'A';
    BinTree B = malloc(sizeof(struct TNode));
    B->Data = 'B';
    BinTree C = malloc(sizeof(struct TNode));
    C->Data = 'C';
    BinTree D = malloc(sizeof(struct TNode));
    D->Data = 'D';
    BinTree E = malloc(sizeof(struct TNode));
    E->Data = 'E';
    BinTree F = malloc(sizeof(struct TNode));
    F->Data = 'F';

    A->Left = B;
    A->Right = C;
    B->Left = D;
    B->Right = E;
    C->Right = F;

    C->Left = NULL;
    D->Left = NULL;
    D->Right = NULL;
    E->Left = NULL;
    E->Right = NULL;
    F->Left = NULL;
    F->Right = NULL;

    printf("中序遍历： ");
    InorderTraversal(A);
    printf("\n");

    printf("先序遍历： ");
    PreorderTraversal(A);
    printf("\n");

    printf("后序遍历： ");
    PostorderTraversal(A);
    printf("\n");

    printf("层次遍历： ");
    LevelorderTraversal(A);
}

2. 输出二叉树的所有叶子结点

// 输出叶结点
// 在先序遍历的基础上加上判断语句
void PreorderPrintLeaves(BinTree BT){
    if(BT){
        // 没有左子树和右子树的结点——叶子节点
        if(BT->Left==NULL&&BT->Right==NULL){
            printf("%c\t",BT->Data);
        }
        PreorderPrintLeaves(BT->Left);
        PreorderPrintLeaves(BT->Right);
    }
}

3.输出树的高度

树的高度 = 左右子树中最高的再加一
左子树的高度 = 左右子树中最高的加一
右子树的高度 = 左右子树中最高的加一

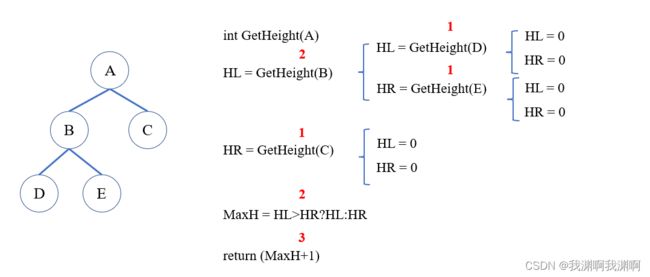
// 输出树的高度
int GetHeight(BinTree BT){
    int HL , HR , MaxH=0;
    if(BT){
        HL = GetHeight(BT->Left);  // 左子树高度
        HR = GetHeight(BT->Right);  // 右子树高度
        MaxH = HL>HR?HL:HR;
        return (MaxH+1);
    } else{
        return 0; // 树为空
    }
}

4.二叉搜索树

二叉搜索树满足以下性质

1. 非空左子树所有键值小于根节点键值
2. 非空右子树所有键值大于根节点键值
3. 左右子树都是二叉搜索树

4.1搜索

// 二叉搜索树查找（递归）
Position Find1(BinTree BST, ElementType X){
    if(BST == NULL) return 0;

    if(X>BST->Data)
        return Find1(BST->Right,X);
    else if(X<BST->Data)
        return Find1(BST->Left,X);
    else if(X==BST->Data)
        return BST; // 查找成功，返回当前结点的地址
}
// 二叉搜索树查找（循环）
Position Find2(BinTree BST, ElementType X){
    while(BST){
        if(X>BST->Data)
            BST = BST->Right;
        else if (X<BST->Data)
            BST = BST->Left;
        else if (X == BST->Data)
            break;
    }
    return BST;
}

4.2插入

// 二叉搜索树的插入
BinTree Insert(BinTree BST, ElementType X){
    if(!BST){
        BST = (BinTree) malloc(sizeof (struct TNode));
        BST->Data = X;
        BST->Right = NULL;
        BST->Left = NULL;
    } else{
        if(X>BST->Data) BST->Right = Insert(BST->Right,X);
        else if(X<BST->Data) BST->Left = Insert(BST->Left,X);
    }
    return BST;

4.3 查找最大最小值

最大值：最右分支的端结点上
最小值：最左分支的端结点上

// 二叉搜索树查找最小值
Position FindMin(BinTree BST){
    if(BST){
        while(BST->Left)
            BST = BST->Left;
        return BST;
    }
}

// 二叉搜索树查找最大值
Position FindMax(BinTree BST){
    if(BST){
        while(BST->Right)
            BST = BST->Right;
        return BST;
    }
}

4.4删除

考虑三种情况

1. 删除叶节点：直接删
2. 删除的结点只有一个孩子节点：删除时需要改变父结点指针
3. 删除的结点有左右两棵子树：取其右子树的最小元素填充或者取其左子树的最大元素填充

BinTree Delete(BinTree BST, ElementType X){
    Position tmp;
    if(BST == NULL) printf("未找到删除元素");
    else{
        if(X<BST->Data)
            BST->Left = Delete(BST->Left,X); // 左子树递归删除
        else if(X>BST->Data)
            BST->Right = Delete(BST->Right,X); // 右子树递归删除
        else{ // 需要删除的结点
            if(BST->Left&&BST->Right){ // 删除的结点有左右子树
                tmp = FindMin(BST->Right);
                BST->Data = tmp->Data;
                BST->Right = Delete(BST->Right,BST->Data); // 从右子树删除最小元素
            } else{ // 被删除的结点有一个或无子结点
                tmp = BST;
                if(!BST->Left)
                    BST = BST->Right;
                else
                    BST = BST->Right;
                free(tmp);
            }
        }
        return BST;
    }
}