python快速两两元素求相似矩阵
目录
- 1. 计算相似度矩阵
- 2. 基于sklearn
1. 计算相似度矩阵
计算相似度矩阵的方法有很多种,发现了sklearn中直接有通过计算余弦相似度得到相似度矩阵的方法
1 sklearn.metrics.pairwise.cosine_similarity # 余弦相似度
2 sklearn.metrics.pairwise.pairwise_distances #余弦距离
>>> from sklearn.metrics.pairwise import cosine_similarity
>>> from sklearn.metrics.pairwise import pairwise_distances
>>> a=[[1,3],[2,2]]
>>> cosine_similarity(a)
array([[ 1. , 0.89442719],
[ 0.89442719, 1. ]])
>>> pairwise_distances(a,metric="cosine")
array([[ 0. , 0.10557281],
[ 0.10557281, 0. ]])
pairwise_distances方法是 cosine_similarity减1后取绝对值得到的。
2. 基于sklearn
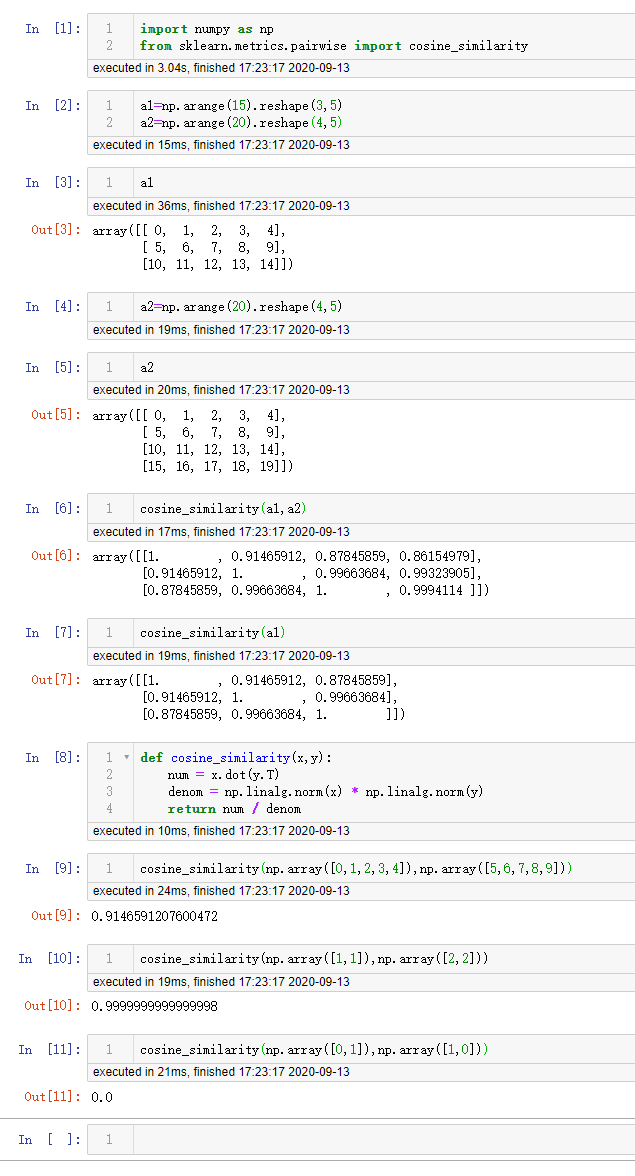
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
a1=np.arange(15).reshape(3, 5)
a2=np.arange(20).reshape(4, 5)
print(cosine_similarity(a1, a2)) # 第一行的值是a1中的第一个行向量与a2中所有的行向量之间的余弦相似度
print(cosine_similarity(a1)) # a1中的行向量之间的两两余弦相似度
a1 和 a2 介绍,a1 包含 3 个元素,a2 包含 4 个元素,
a1
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
a2
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
cosine_similarity(a1) # 3 × 3
Out[3]:
array([[1. , 0.91465912, 0.87845859],
[0.91465912, 1. , 0.99663684],
[0.87845859, 0.99663684, 1. ]])
cosine_similarity(a1, a2) # 3 × 4
Out[2]:
array([[1. , 0.91465912, 0.87845859, 0.86154979],
[0.91465912, 1. , 0.99663684, 0.99323905],
[0.87845859, 0.99663684, 1. , 0.9994114 ]])
cosine_similarity(a1) 将是 a1 的 3 个元素相互计算余弦相似度,而 cosine_similarity(a1,a2) 则是 a1 的 3 个元素和 a2 的 4 个元素相互进行余弦相似度计算。
[1] 在 numpy 中,对数组或矩阵中的每个元素,进行函数计算 2019.12;
[2] python计算相似矩阵 2018.6;
[3] python向量之间相似性的计算方法(持续更新中)2019.1;
[4] Python 使用sklearn计算余弦相似度 2020.9;