【刷题之路Ⅱ】百度面试题——迷宫问题

一、题目描述

原题连接： 迷宫问题
题目描述：
定义一个二维数组 N*M ，如 5 × 5 数组下所示：
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};

它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的路线。入口点为[0,0],既第一格是可以走的路。

数据范围：
2≤n,m≤10 ， 输入的内容只包含 0≤val≤1

输入描述:

输入两个整数，分别表示二维数组的行数，列数。再输入相应的数组，其中的1表示墙壁，0表示可以走的路。数据保证有唯一解,不考虑有多解的情况，即迷宫只有一条通道。

输出描述:
左上角到右下角的最短路径，格式如样例所示。

示例1

输入
5 5
0 1 0 0 0
0 1 1 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出
(0,0)
(1,0)
(2,0)
(2,1)
(2,2)
(2,3)
(2,4)
(3,4)
(4,4)

示例2

输入
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 1
0 1 1 1 0
0 0 0 0 0
输出
(0,0)
(1,0)
(2,0)
(3,0)
(4,0)
(4,1)
(4,2)
(4,3)
(4,4)

说明
注意：不能斜着走！！

二、解题

1、方法1——暴力递归

解决这道题我采用的是比较暴力的方法，就是将所有的路都走一遍，因为题目只要求求出一条通路，所以只需要直到一条通路就可以结束了。

1.1、思路分析

那我们要怎样设计递归算法呢？
因为题目是要求我们将路径的坐标依次打印出来，所以很容易想到的就是将走过的路径的坐标依次压入栈中，例如：

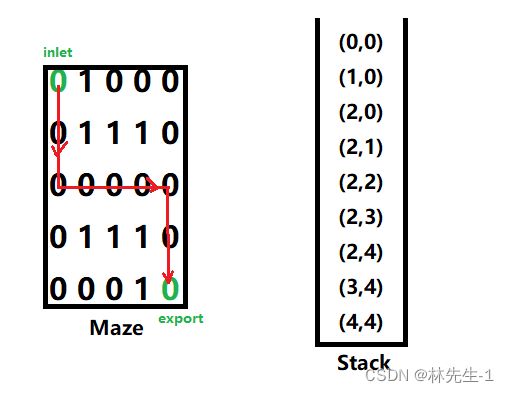
只不过最后找到通路后的打印要想将栈中的元素逆置过来再打印。

如果走到某个坐标发现走到了死胡同(上下左右四个方向都走不通)，那我们就将当前坐标弹出栈中，返回到上一个坐标继续判断有没有通路。
而为了避免“走回头路”而发生的死递归问题，我们需要将访问过的Maze的坐标的值改成2(其实改成任何数都可以，只要不要改成0就可以)：

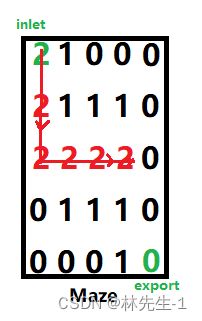
然后因为我们要压入栈中的是坐标，所以我们可以定义一个结构体pos，来保存Maze中每个元素对应的横坐标与纵坐标：

typedef struct position {
    int row;
    int col;
} pos;

然后我们就将栈的存储类型改成pos即可。

那我们主要的思路有了，那我们应该怎样设计算法呢？
其实我们主要要实现的只有一个函数——找通路的函数GetPath。
我们在GetPath函数里递归调用上下左右四个方向的找通路，如果当前被调用的坐标等于出口坐标就可以返回，而主要上下左右有任何一个方向的递归调用找到了通路就可以返回(同时最重要的是要先判断坐标的有效性)。

接下来还是看具体的代码实现吧：

1.2、先将栈实现一下

没办法，我用的是C语言，所以还是先要自己造轮子，这其实就只是个CV工程而已：

// 定义一个坐标结构体
typedef struct position {
    int row;
    int col;
} pos;
// 先要将栈实现一下
// 重定义数据类型
typedef pos DataType;

// 定义栈结构
typedef struct stack {
    DataType* data;
    int top;
    int capacity;
} Stack;

// 栈的初始化
void StackInit(Stack* ps);

// 压栈
void StackPush(Stack* ps, DataType x);
// 弹栈
void StackPop(Stack* ps);
// 返回栈顶数据
DataType StackTop(Stack* ps);
// 返回栈的数据个数
int StackSize(Stack* ps);
// 判断栈是否为空
bool StackEmpty(Stack* ps);
// 栈的销毁
void DestroyStack(Stack* ps);

// 栈的初始化
void StackInit(Stack* ps) {
    assert(ps);
    ps->data = NULL;
    ps->top = 0;
    ps->capacity = 0;
}

// 压栈
void StackPush(Stack* ps, DataType x) {
    assert(ps);
    // 检查是否需要增容
    if (ps->top == ps->capacity) {
        int newCapacity = ps->capacity == 0 ? 10 : ps->capacity * 2;
        DataType* temp = (DataType*)realloc(ps->data, newCapacity * sizeof(DataType));
        if (NULL == temp) {
            perror("ralloc fail!\n");
            exit(-1);
        }
        ps->data = temp;
        ps->capacity = newCapacity;
    }
    ps->data[ps->top] = x;
    ps->top++;
}

// 弹栈
void StackPop(Stack* ps) {
    assert(ps);
    assert(ps->top > 0);
    ps->top--;
}

// 返回栈顶数据
DataType StackTop(Stack* ps) {
    assert(ps);
    assert(!StackEmpty(ps));
    return ps->data[ps->top - 1];
}

// 返回栈的数据个数
int StackSize(Stack* ps) {
    assert(ps);
    assert(ps->top >= 0);
    return ps->top;
}

// 判断栈是否为空
bool StackEmpty(Stack* ps) {
    assert(ps);
    return ps->top == 0;
}

// 栈的销毁
void DestroyStack(Stack* ps) {
    assert(ps);
    free(ps->data);
    ps->data = NULL;
    ps->top = 0;
    ps->capacity = 0;
}

1.3、代码实现

因为我们要在多个函数之中使用同一个栈，而每次传参都传一个栈的话就有点太麻烦了。所以我们可以直接将栈定义成全局的。
注意 ：因为这里是io型的oj题，所以我们没必要在main函数中最开始就将栈初始化，如果是接口型的oj题，就一定要在main函数中先将栈初始化，不然最多只能过一个测试用例。

// 先定义一个全局栈
Stack pathStack;

main函数：

int main() {
    int Row = 0;
    int Col = 0;
    while (scanf("%d %d", &Row, &Col) != EOF) {
        int** path = (int**)malloc(Row * sizeof(int*));
        if (NULL == path) {
            perror("malloc fail!\n");
            exit(-1);
        }
        int i = 0;
        for (i = 0; i < Row; i++) {
            path[i] = (int*)malloc(Col * sizeof(int));
            if (NULL == path[i]) {
                perror("malloc fail!\n");
                exit(-1);
            }
        }
        int j = 0;
        for (i = 0; i < Row; i++) {
            for (j = 0; j < Col; j++) {
                scanf("%d", &path[i][j]);
            }
        }
        pos entry = { 0 , 0 }; // 入口
        if (GetPath(path, Row, Col, entry)) {
            printPath();
        }
        else {
            printf("没有找到通路\n");
        }
    }
    DestroyStack(&pathStack);
}

找通路函数GetPath：

bool GetPath(int** path, int row, int col, pos cur) {
    assert(path);
    StackPush(&pathStack, cur);
    if (cur.row == row - 1 && cur.col == col - 1) {
        return true;
    }
    path[cur.row][cur.col] = 2;

    // 判断当前坐标的上下左右四个方向是否能走

    pos next = { 0, 0 };

    next = cur;
    // 上
    next.row += 1;
    if (isPass(path, row, col, next)) {
        if (GetPath(path, row, col, next)) {
            return true;
        }
    }

    next = cur;
    // 下
    next.row -= 1;
    if (isPass(path, row, col, next)) {
        if (GetPath(path, row, col, next)) {
            return true;
        }
    }

    next = cur;
    // 左
    next.col -= 1;
    if (isPass(path, row, col, next)) {
        if (GetPath(path, row, col, next)) {
            return true;
        }
    }

    next = cur;
    // 右
    next.col += 1;
    if (isPass(path, row, col, next)) {
        if (GetPath(path, row, col, next)) {
            return true;
        }
    }

    StackPop(&pathStack);
    return false;
}

判断坐标是否能走：

bool isPass(int** path, int row, int col, pos cur) {
    assert(path);
    if ((cur.row >= 0 && cur.row < row)
        && (cur.col >= 0 && cur.col < col)
        && path[cur.row][cur.col] == 0) {
        return true;
    }
    return false;
}

打印通路：

void printPath() {
    Stack RPathStack;
    StackInit(&RPathStack);

    // 将PathStack栈中的数据全都压入RPathStack栈中
    while (!StackEmpty(&pathStack)) {
        StackPush(&RPathStack, StackTop(&pathStack));
        StackPop(&pathStack);
    }

    pos cur = { 0, 0 };
    // 再将RPathStack栈中的数据取出来打印
    while (!StackEmpty(&RPathStack)) {
        cur = StackTop(&RPathStack);
        StackPop(&RPathStack);
        printf("(%d,%d)\n", cur.row, cur.col);
    }
    DestroyStack(&RPathStack);
}```