Codeforces Round 863 (Div. 3)
A. Insert Digit
题意:给定一个数字字符串s和一个数字d,将d找一个位置插入,让这个字符串的数值达到最大。
思路:关键点在于找到字符插入的位置,字符插入后字符串会多一位,所以目的是尽可能让高位的字符串的数值大。也就是说,字符串插入的位置的左边的数都是高位,应该都比当前要插入的数大。所以问题也就演变成了查找第一个小于d的字符的位置,或者说是查找最后一个大于d的字符,让d插入到这个数后面。
这里区分一下查找第一个小于d的字符和查找最后一个大于的d字符:
如果查找第一个小于d的字符,那么还需要考虑s中所有字符都大于d的情况,那么找不到字符的情况下,插入d还需要另加判断条件。不如直接找d的前驱字符,一开始令下标index为0,然后遍历s,如果找到了大于d的字符,就让index = 这个字符的下标+1(因为d可能要往这个字符后面插入),一直到查找到第一个小于d的字符或者到了s的结尾终止遍历,此时index的位置就是要插入的位置。
先放第一次提交的代码
#include
using namespace std;
typedef vector vi;
typedef long long int ll;
typedef vector vb;
typedef vector vll;
typedef vector vvll;
typedef pair pii;
typedef vector vpii;
int main(){
int N;
cin >> N;
while (N--){
int n;
char d;
cin >> n >> d;
for (int i = 0; i < n; ++i){
char t;
cin >> t;
if (d >= 0 && t < d){
cout << d << t;
d = -1;
}
else cout << t;
}
if (d >= 0) cout << d;
cout << endl;
}
return 0;
}
第一次思考的时候就是想着找第一个小于d的字符,并且边输入边输出,有点繁琐,而且没有将cin和cout加到stdio里面,时间用的比较久,大概500ms。
修改后的代码:
#include
using namespace std;
typedef vector vi;
typedef long long int ll;
typedef vector vb;
typedef vector vll;
typedef vector vvll;
typedef pair pii;
typedef vector vpii;
int get_level(int x, int y, int n){
if (x > n / 2) x = n + 1 - x;
if (y > n / 2) y = n + 1 - y;
return min(x, y);
}
int main(){
int N;
cin >> N;
while (N--){
int n;
char d;
cin >> n >> d;
string s;
cin >> s;
int index = 0;
for (int i = 0; i < n; ++i){
if (s[i] < d) break;
index = i + 1;
}
s.insert(s.begin() + index, d);
cout << s << endl;
}
return 0;
}
简洁了很多,用时也由500ms降到了60ms。
总结:这道题目的关键在于找插入位置的方法。一开始看到将字符插入到串中让串最大是有点懵的,没有思考过这类的问题。后来看了测试数据发现插入的位置就是第一个小于他的数前面,但是当时做题还没有将思路转换为找到最后一个大于他的数。所以做题的时候分析是很重要的,不能一股脑的想一出来一出,凭着主观经验来解决。要把问题进行分解和判断,再根据问题的特性找出更优的解决方法。
B. Conveyor Belts
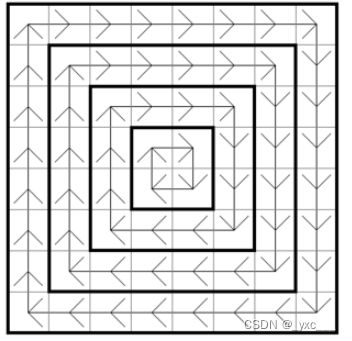
给定一个n阶的方阵,n是偶数。方阵是一个由方环组成的图形,其中每个环都代表了一个层级,比如中心是第一层,外面一层是第二层,再往外一层是第三层,以此类推。其中当人站在方环中时会按着顺时针的方向在该层中不断的自动移动,但是不会越出该层。
如果想要从当前层到达另一个层,需要消耗一个能量。
现在给出一组坐标x,y和x1,y1。判断从xy到x1y1最少需要消耗多少能量。
思路:根据起始坐标可以判断出当前所在层的层级,终止坐标也是。只要判断出两个层的层级,就可以知道从起始到终点需要消耗多少能量。因为人在同一层级内是会不断的流动而不会越出当前层级,所以只要到达了目标层级,就一定会随着时间流动到目标坐标。于是问题演变成了,根据坐标点推算起点和终点的层级。
不难发现:给定一组坐标xy,当前坐标所处的层级就是xy中较小值的坐标。假设最外层的层级为1,那么坐标(4,3)一定在第3层级,坐标(2,1)一定在第一层级,这种坐标只适用于坐标位于矩阵左上角的情况,比如(2,8)也是第一层级,但是2是坐标中的较小值,按照上面的推论,(2,8)应该在第二层级。所以我们需要将给出的坐标映射到矩阵的左上角,然后就可以判断坐标所属的层级。对于n为8的矩阵,分别给出x和y的映射方式(只有当x和y不在左上角时才可以计算,所以计算前要加一个判断条件):x = 0 + n + 1 - x, y = 0 + n + 1 - y;这样就可以将坐标对应到左上角,然后进行判断层级即可。这种计算方式是有简单的数学逻辑在里面,就是计算出当前格子到终点有多少个格子,然后将这个格子数关于中心对称对应到了从起点开始。
上代码:
#include
using namespace std;
typedef vector vi;
typedef long long int ll;
typedef vector vb;
typedef vector vll;
typedef vector vvll;
typedef pair pii;
typedef vector vpii;
int get_level(int x, int y, int n){
if (x > n / 2) x = n + 1 - x;
if (y > n / 2) y = n + 1 - y;
return min(x, y);
}
int main(){
int N;
cin >> N;
while (N--){
int n, x1, y1, x2, y2;
cin >> n >> x1 >> y1 >> x2 >> y2;
int start = get_level(x1, y1, n);
int endd = get_level(x2, y2, n);
cout << abs(endd - start) << endl;
}
return 0;
}
总结:英文不好,题目晦涩难读懂,读了好几遍才理解。
C. Restore the Array
题意:给定一个长度为n - 1的数组b,这个数组中每个元素由一个长度为n的数组a计算得出,其中
b[i] = max(a[i], a[i] + 1)。给出数组b,输出数组a。
思路:题目有一种构造的感觉,题解肯定不唯一,于是要找出构造的规则,来推出数组a。
从数组b的数据入手,对于每个b[i]来说,他由a[i]或者a[i + 1]构成,
对于下标从0开始的数组b,对于i∈[1, n - 2]
如果b[i] > b[i - 1],那么b[i]一定由a[i + 1]构造。(因为如果由a[i - 1]构造的话,那么b[i -1]必然跟a[i]相等)
否则,a[i] = b[i]
然后让a[0] = b[0], a[n - 1] = b [n -2]即可。
#include
using namespace std;
typedef vector vi;
typedef long long int ll;
typedef vector vb;
typedef vector vll;
typedef vector vvll;
int main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int N;
cin >> N;
while (N--){
int n;
cin >> n;
vi b(n - 1), a(n, 0);
for (int i = 0; i < n - 1; ++i) cin >> b[i];
a[0] = b[0];
for (int i = 1; i < n - 1; ++i){
if (b[i] > b[i - 1]){a[i + 1] = b[i];}
else{a[i] = b[i];}
}
for (int i = 0; i < n; ++i){
cout << a[i] << " \n"[i + 1 == n];
}
}
return 0;
}
总结:这个题目对于做题少的人来说很考验临场的逻辑推敲能力,在思考的时候用了很多错误的方式。
这个题的思考思路应该是这样:
已知的数据为b,应该由b推出a的每个元素,而b的每两个相邻元素可以确定一个a的元素,所以考虑两个相邻元素的关系,可以确定出a的数据。如果前面小于后面,那么这两个元素的贡献一定由不同的a给予,所以左边的a就一定不是后面的b值,那么右边的a就一定是后面b值。而对于小于或者等于的情况,就把小值放在左边的a上面。
这里还有一个疑问,就是对于b[i - 1] > b[i]而言,b[i - 1]一定由a[i - 1]确定,如果由a[i ]确定,那么b[i]一定等于b[i -1],矛盾。所以b[i]可以由a[i]或者a[i + 1]得到。这里选择a[i]作为b[i]的值,因为如果选择a[i + 1]作为b[i]的值,那么还要将a[i]设为一个更小的值,会多一些多余操作出来,而且如果选择了a[i + 1]作为b[i]的值,那么b[i + 1]一定要大于或者等于b[i],因为b[i + 1] 由a[i + 1] 和a[i + 2]贡献而成。所以考虑每个b[i]的时候,合理的构造方式是对后面的构造不产生影响的,不然会造成计算的混乱跟多余。
是个很经典的思考题...
D. Umka and a Long Flight
题意:给定一个数字n,第n和第n+1个fibonacci数分别代表举行的height和width。然后给出x和y,表示在举行的x行y列涂上颜色。
问,能否通过以下方式裁剪,让裁剪得到的矩形数量刚好是n + 1个:
1、 每个涂了颜色的小方块的边长都为1
2、最多有一对边长相等的正方形
3、每个正方形的边长必须是fibonacci数
思路:根据n可以得到矩形的height和width,然后根据涂了的颜色可以得到小方块的数量,然后....
#include
using namespace std;
typedef vector vi;
typedef long long int ll;
typedef vector vb;
typedef vector vll;
typedef vector vvll;
typedef pair pii;
typedef vector vpii;
int main(){
int N;
cin >> N;
while (N--){
int n, x, y;
cin >> n >> x >> y;
ll height = 1, width = 1;
map mapp;
if (n >= 2){
for(int i = 2; i <= n; ++i){
int t = height + width;
width = height;
height = t;
mapp[width] = mapp[height] = false;
}
}
int cnt = height + width - 1;
}
return 0;
}
总结:今天写文章发现上面求的Height,和width是第n和第n-1个Fibonacci数,之前看错题了,然后涂了颜色的小方块数量的话好像绝对是大于n+1个的,因为一行+一列再减去1一定是大于n+1的?然后等后续再思考吧
E. Living Sequence
题意:日本人觉得4这个数不吉利,于是把所有包含4的数字从数学中删除了。比如第4个数是5,第12个数是15。给出一个数字k,问这个数再日本人的数字里是几?
思路:删除了包含了4的数字后所有的数字都进行了向前平移,如果能够知道当前的第k位数字是后面哪个数往前平移得到的,就可以O(1)的计算出这个数。但是应该先预处理一下每个数字区间的数字往前移动的位数?不太确定