便利蜂2022.3.17笔试

题目一

1、题目描述

2、算法分析

2.1、解法1：直接暴力

总的空间是Y，现在有N个物品，每个物品的占用空间为P，数量为NUM。现在想要满足在不超过Y的条件下，能够放进去最多的物品数量是多少？

我们可以容易想到，要想在总空间一定的条件下，尽可能的放进去更多的物品，那么我们应该优先选择占用空间小的物品，当这些物品选完了，然后总空间还有剩余，我们才进一步考虑占用空间大的其他物品。

import java.io.*;
import java.util.*;
class Test{

    public static void main(String[] args)
    {
        Scanner sc = new Scanner(System.in);
        int y =sc.nextInt();//总的空间资源
        int n =sc.nextInt();//商品种类数目
        int [] value = new int[n];
        int [] nums = new int[n];
        //定义一个nx2的矩阵来存储b组物品的空间资源大小和数量
        int[][] arr = new int[n][2];
        for(int i=0;i(o1[0]-o2[0]));
        //表示最多可以放的商品个数
        int ans =0;

        int curW = 0;
        for(int i=0; i= y){
                break;
            }else{
                int tmp = (y-curW)/arr[i][0]; //求的当前剩余空间资源 可以放多少个当前物品
                if(tmp < arr[i][1]){ //如果剩余空间 计算得到可以放当前物品的个数tmp 小于该物品的数量上限，则把tmp个物品都放进
                    ans += tmp;
                    curW += tmp*arr[i][0];
                }else{ //如果计算的tmp 大于等于 该物品的数量上限，说明没有这么多个tmp商品，最多最能放进arr[i][1]个物品
                    ans += arr[i][1];
                    curW += arr[i][0] * arr[i][1];
                }
            }


        }

        System.out.println(ans);
    }
}

2.2、解法2：多重背包===》转为为01背包

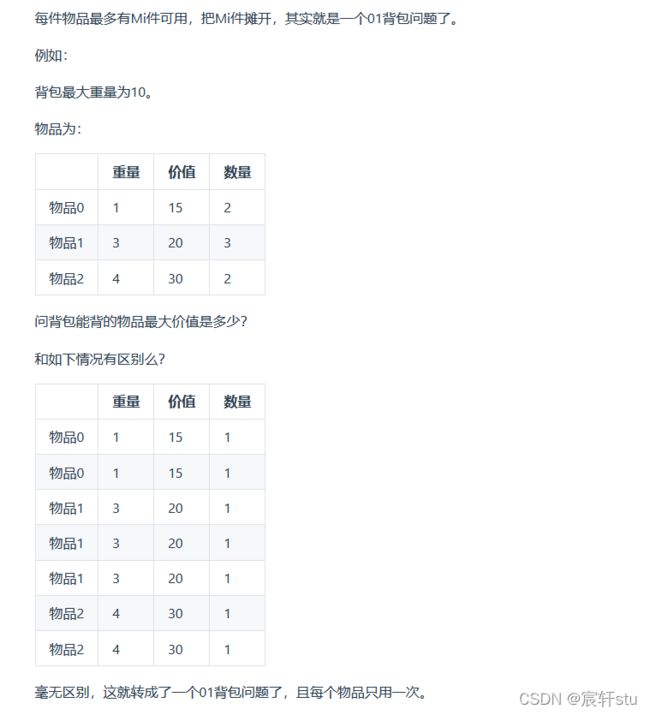
我们知道01背包问题，物品的数量视为1，拿了就没了。本题的每一个物品却有数量限制，每件物品的数量为Num,那么我们把num件物品摊开，就可以构成01背包问题。

举例说明：

 所以，本题我们可以根据每件物品的数量，把其对应占用的空间资源展平，构成每件物品数量为1，空间资源为P，总的空间资源为Y的01背包问题，求装满Y的条件下，使用到的物品数量最多。

import java.io.*;
import java.util.*;
class Test{
    
    public static void main(String[] args)
    {
        Scanner sc = new Scanner(System.in);
        int y =sc.nextInt();//总空间
        int n =sc.nextInt();//物品种类数
        List value = new ArrayList<>();//每件物品占用的空间资源
        List nums = new ArrayList<>();//每件物品对应的数量
        for(int i=0;i1){
                        //物品数量大于1，展开
                        //相当于当前物品有num个，我们就在value增加num-1个value(i)进去，
                        //此时每个value(i)数量都为1，变成01背包
                        value.add(value.get(i));
                        nums.set(i,nums.get(i)-1);
                    } 
            }

        }
        
        // dp[j]表示当前总空间资源为j，能够放进去的最多物品数量
        int[] dp = new int[y+1];//总的空间资源大小
        for(int i=0;i=value.get(i);j--){//总空间，压缩dp，这里要倒序，防止物品多次加入
                dp[j]=Math.max(dp[j],dp[j-value.get(i)]+1);//可以选择放 或者不放
            }
        }
        
       System.out.println(dp[y]);

       
    }
    
}

=================================================================

题目二

1、题目描述

GG   没时间做了！！！直接到第三题

===================================================================

题目3

1、题目描述

2、算法分析

2.1、解法1 ：回溯+筛选

其实拿到这样的题，就是一个求组合的问题，只不过这里最后要的结果是这些组合里面最小的那个。涉及到组合、子集、排列、分割等问题，我们自然而然想到了回溯算法。

解题流程：

第一步：本题我先采用回溯算法，从数组arr中，选出某几个数值组合的数值之和>=Y的这些子集，存到总的可能结果集中；

第二步：从满足条件的结果集中，挑选出子集元素之和最小的即可（因为结果集中的每一个子集都满足元素之和大于等于优惠劵需求Y，这里要求我们尽可能少的消费拿到优惠劵，跳出子集元素之和最小的，也就是我们的最小消费了）

import java.io.*;
import java.util.*;
class Test{

    public static void main(String[] args)
    {
        Scanner sc = new Scanner(System.in);
        int n =sc.nextInt();
        int y =sc.nextInt();
        int [] value = new int[n];
        for(int i=0;i> result = new ArrayList<>();
        LinkedList path = new LinkedList<>();
        
        backtrack(result,path,value,y,0,0);
        int ans = Integer.MAX_VALUE;
        List list = new ArrayList<>();
        for(int i=0;itmp ? tmp:ans;
            
        }
       
       System.out.println(ans);

       
    }
    
    private static void backtrack(List> result, LinkedList path,int[] arr ,int y,int startIdx,int sum){
        if(sum>=y){
            result.add(new ArrayList<>(path));
            return;
        }
        
        for(int i=startIdx;i

2.2、解法2 ：回溯+筛选（在解法1基础优化）

上面的解法中，我们可以发现，我们先回溯算法保存了一个满足最低消费要求的所有结果子集，然后又从这一堆结果集中选出 元素之和最小的那个子集，这个最小元素之和就是 我们要满足约束条件可以得到的最低花费。

其实，进一步思考，我们可以发现，我们绕了一个圈，额外花费了很多空间来保存满足条件的结果集 ，绕绕转转 最后还是回到了找到满足条件子集中元素之和最小的，返回这个最小元素之和的值。

那么我们为什么还要去花费空间保存满足条件的所有结果集，，我们要的只是满足条件的所有可能中的最小花费，所以我们可以在回溯的过程中就直接保存满足条件的每个子集的元素之和，最后选择最小的那个就是答案！！！！

import java.io.*;
import java.util.*;
class Test{
    
    public static void main(String[] args)
    {
        Scanner sc = new Scanner(System.in);
        int n =sc.nextInt();
        int y =sc.nextInt();
        int [] value = new int[n];
        for(int i=0;i list = new ArrayList<>();//存放所有满足条件的子集sum，，最后获取最小的sum就是我们的最少花费
       LinkedList path = new LinkedList<>();//临时维护的满足条件的子集
       int sum =0;//临时维护的子集元素之和
        
        //回溯算法
        backtrack(list,path,value,y,0,0);
        //list排序
        Collections.sort(list, new Comparator() {
            @Override
            public int compare(Integer o1, Integer o2) {
            	return o1 > o2 ? 1:-1;
            }
        });

        
       System.out.println(list.get(0));

       
    }
    

    
    public static void backtrack( List list,LinkedList path,int[] arr ,int y,int startIdx,int sum){
        if(sum>=y){ //如果当前子集path元素之和大于等于y，满足消费门槛了，该子集保存到结果集中作为候选
            list.add(sum);
            return;
        }
        
        //递归 回溯
        for(int i=startIdx;i

解法2 优化三：

        其实上面的代码还可以继续优化，我们要的只是满足约束条件的所有组合子集中，子集元素之和最小值，所以我们其实没有必要新建一个list来存储所有满足约束的子集的元素之和，然后再从这个元素和中选出最小的一个。（这里就又又绕圈的感觉了！！）

        为什么要存所有满足约束 的组合子集的元素和，然后再去挑最小的，这么傻了吗？？所以我们可以直接用一个全局变量来维护 当前满足条件的所有组合子集中 元素和最小值，，回溯结束，那我们子集最小值也维护结束，直接输出这个全局变量就是结果！！！！！！