用python写一个连通图的最短路径以及费用问题

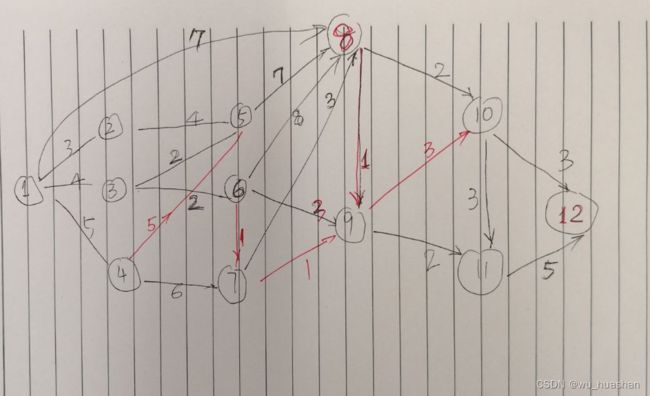
假设有12个城市，相互联通的情况如图所示。假设只能从小号城市到大号城市单向。按照手工绘图情况，初始化pay矩阵用来记录任意两个城市之间的最短路径或者费用。

pay = []  # 保存两个站点之间的路费
path = []  # 保存两个站点之间的行走路径（确保最少费用）
MAX = 500000  # 假设两个站点不通，则设置路费为50万元表示无穷大。
STATIONS = 12  # 设置12个站点，可以自己扩充

#初始化任意两个站点之间的距离或者路费
#设置一个0号站点，到任意站点0~12的距离或者费用为MAX
pay.append([MAX, MAX, MAX, MAX, MAX, MAX, MAX, MAX, MAX, MAX, MAX, MAX, MAX])

#设置一个1号站点，到任意站点0~12的距离或者费用为MAX
pay.append([MAX, 0, 3, 4, 5, MAX, MAX, MAX, 7, MAX, MAX, MAX, MAX])

# 2号站点，到任意站点0~12的距离或者费用
pay.append([MAX, MAX, 0, MAX, MAX, 4, MAX, MAX, MAX, MAX, MAX, MAX, MAX])

# 3号站点，到任意站点0~12的距离或者费用
pay.append([MAX, MAX, MAX, 0, MAX, 2, 2, MAX, MAX, MAX,    MAX, MAX, MAX])

# 4号站点，到任意站点0~12的距离或者费用
pay.append([MAX, MAX, MAX, MAX, 0,  MAX, 5, 6, MAX, MAX, MAX, MAX, MAX])

#5
pay.append([MAX, MAX, MAX, MAX,  MAX,  0, MAX,  MAX, 7, MAX, MAX, MAX, MAX])

#6
pay.append([MAX, MAX, MAX, MAX,  MAX,  MAX, 0,  1, 8, 3, MAX, MAX, MAX])

#7
pay.append([MAX, MAX, MAX, MAX,  MAX,  MAX,  MAX,  0, 3, 1, MAX, MAX, MAX])

#8
pay.append([MAX, MAX, MAX, MAX,  MAX,  MAX,  MAX, MAX, 0, 1, 2, MAX, MAX])

#9
pay.append([MAX, MAX, MAX, MAX,  MAX,  MAX,  MAX, MAX, MAX, 0, 3, 2, MAX])

#10
pay.append([MAX, MAX, MAX, MAX,  MAX,  MAX,  MAX, MAX, MAX, MAX, 0, 3, 3])

# 11号站点，到任意站点0~12的距离或者费用
pay.append([MAX, MAX, MAX, MAX,  MAX,  MAX,  MAX, MAX, MAX, MAX, MAX, 0, 5])

#路费设置完毕

#初始化两个站点之间的路径对应的站点集合，例如站点3--7 ，则path[3][7]=[3,7]
for x in range(STATIONS+1):
    temp = []
    for y in range(STATIONS+1):
        temp.append([x, y])
    path.append(temp)

#分析每个站点到终点站的最少费用所经过的站点集合
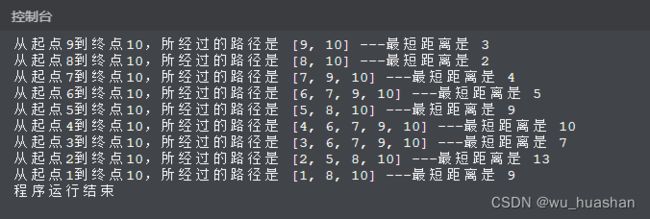
over=12   #分别修改over=11 10  则表示终点是11号或者10号
last = over-1
while last > 0:
    minpay = pay[last][over]
    for nextnumber in range(last+1, over):
        if pay[nextnumber][over]+pay[last][nextnumber] < minpay:
            minpay = pay[nextnumber][over]+pay[last][nextnumber]
            pay[last][over] = minpay
            #print(last,nextnumber,STATIONS)
            path[last][over] = [last]+path[nextnumber][over]
    last = last-1
k = over-1
while k > 0:
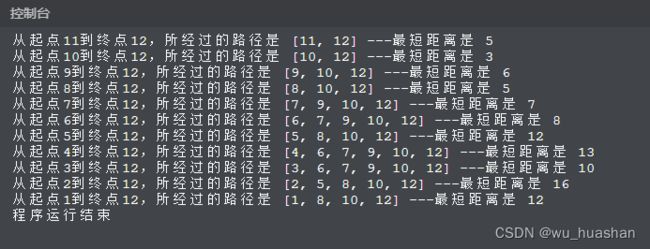
    print('从起点%d到终点%d，所经过的路径是' %(k,over), path[k][over], '---最短距离是',pay[k][over])
 
    k = k-1