匈牙利算法相关介绍
重要说明：本文从网上资料整理而来，仅记录博主学习相关知识点的过程，侵删。
一、参考资料
匈牙利算法匹配问题?
Exactly how the Hungarian Algorithm works
多目标跟踪数据关联之匈牙利算法
五分钟小知识：什么是匈牙利算法
论文：The Hungarian Method for the Assignment Problem
二、相关介绍
1. 二分图
1.1 二分图的概念
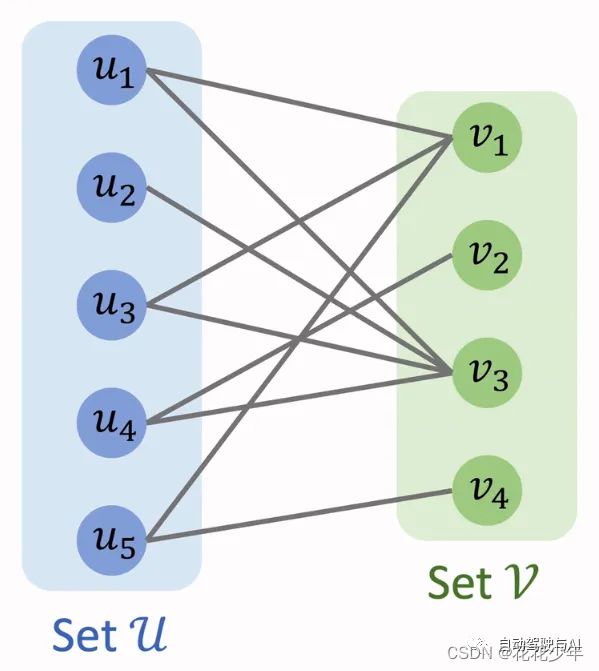
二分图（Bipartite Graph）又称作二部图，是图论中的一种特殊模型。二分图的顶点集可以被划分为两个互不相交的独立子集 U 和 V ：
G = ( U , V , E ) G=(U,V,E) G=(U,V,E)
二分图边集合 E 中的每一条边分别连接了顶点子集 U 和 V 中的一个顶点，但 U 和 V 内部的顶点互不相连。一个典型的二分图如下所示：
简单来说，如果图中所有顶点可以被分为两个集合，图中所有的边的头和尾不属于同一个顶点集合，而是跨越两个集合，则这个图是一个二分图。
1.2 无向图生成二分图
无向图如下所示：
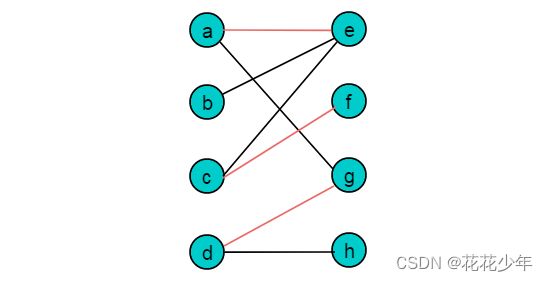
将顶点a，b，c，d作为集合A，将e，f，g，h作为集合B，转换为二分图：
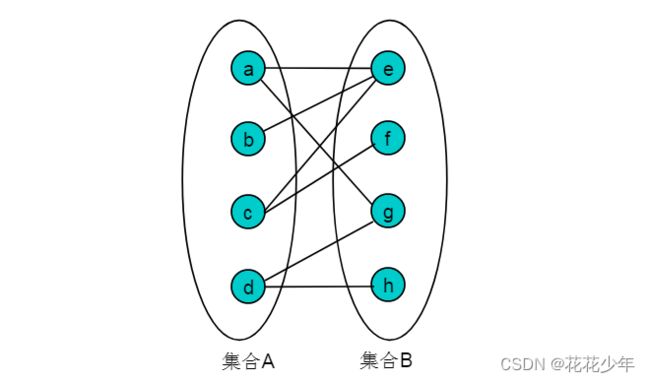
可以看出，图中顶点可以划分为A，B两个集合，而任意一条边的头和尾又分别隶属于集合A和集合B，因此，此图为二分图。
1.3 判定二分图
判定一个图是否是二分图等价于判定该图是否是二色图，即图中所有顶点是否能被染色成两类颜色（需要保证相连顶点不能同色），可以通过广度优先搜索（Breadth First Search，BFS）实现。
C++代码示例，使用邻接表来存储图，时间复杂度为O(V+E)。
#include
#include
#include
#include
/**
* @brief 用于判断输入的图是否是二分图
*
* @param V 图的顶点数量
* @param adj 图的邻接表表示
* @return bool 图是否是二分图：true - 是，false - 不是
*/
bool IsBipartite(int V, std::vector adj[])
{
// 存储所有顶点颜色的 vector 容器，初值 -1 表示未染色，0 表示红色，1 表示蓝色
std::vector col(V, -1);
// 用于 BFS 过程的 FIFO 队列，元素类型是顶点索引及其颜色组成的二元组
std::queue> q;
// 遍历所有顶点
for (int i = 0; i < V; i++)
{
// 顶点 i 尚未染色
if (col[i] == -1)
{
// 将顶点 i 染成红色 0，并将其压入 BFS FIFO 队列
col[i] = 0;
q.push({ i, 0 });
// 处理 BFS FIFO 队列中的各顶点
while (!q.empty())
{
auto p = q.front();
q.pop();
// 当前顶点
int v = p.first;
// 当前顶点的颜色
int c = p.second;
// 遍历当前顶点的所有相连顶点
for (int j : adj[v])
{
// 若相连顶点 j 与当前顶点颜色相同，则输入的图不是二分图
if (col[j] == c) return false;
// 若相连顶点 j 尚未染色
if (col[j] == -1)
{
// 将相连顶点 j 染成与当前顶点颜色相反的颜色，并将其压入 BFS
// FIFO 队列
col[j] = 1 - c;
q.push({ j, col[j] });
}
}
}
}
}
return true;
}
int main()
{
int V, E;
V = 4 , E = 8;
// 使用邻接表存储图
std::vector adj[V];
adj[0] = {1, 3};
adj[1] = {0, 2};
adj[2] = {1, 3};
adj[3] = {0, 2};
IsBipartite(V, adj) ? std::cout << "输入的图是二分图" << std::endl
: std::cout << "输入的图不是二分图" << std::endl;
return 0;
}
2. 二分图匹配
2.1 匹配
在图论中，一个匹配（matching）是指一个边的集合，其中任意两条边都没有公共顶点。
如下图所示，寻找该二分图的一个匹配。
下图中，红色的边为一个匹配。
2.2 匹配点与匹配边
给定图 G = ( V , E ) G=(V,E) G=(V,E)，它的一个匹配（Matching） M \text{M} M 表示包含于边集合 E \text{E} E 的一个子集，即M 由 E \text{E} E 中的若干条边组成：
M ⊆ E M\subseteq E M⊆E
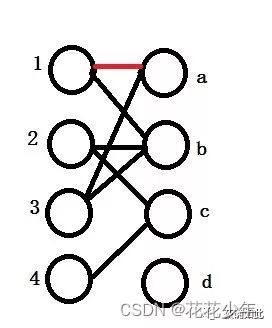
匹配中的任意两条边之间没有公共顶点。下图中的两条红色边构成了它的一个匹配：
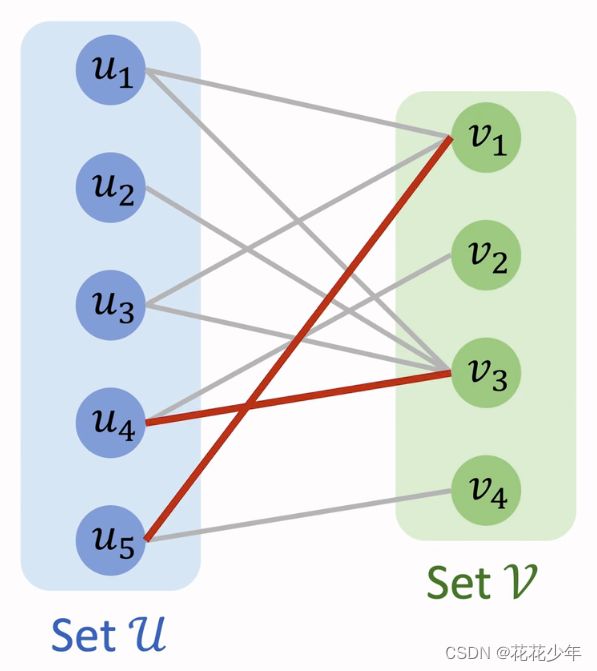
匹配 M \text{M} M 中的边被称为匹配边，上图中的两条红色边都是匹配边；边集合 E \text{E} E 中不属于匹配 M \text{M} M 的边被称为未匹配边，上图中的灰色边都是未匹配边。
匹配边的端点被称为匹配点，上图中顶点 u 4 、 u 5 、 v 1 、 v 3 u_4\text{、}u_5\text{、}v_1\text{、}v_3 u4、u5、v1、v3 都是匹配点；顶点集合 U \text U U 和 V \text V V 中不是匹配边端点的其它顶点被称为未匹配点，上图中顶点 u 1 , u 2 , u 3 , v 2 , v 4 u_1,u_2,u_3,v_2,v_4 u1,u2,u3,v2,v4 都是未匹配点。
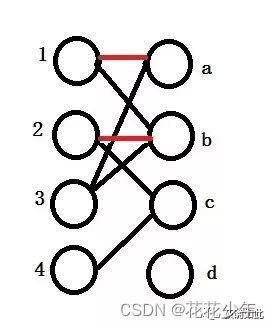
2.3 最大匹配
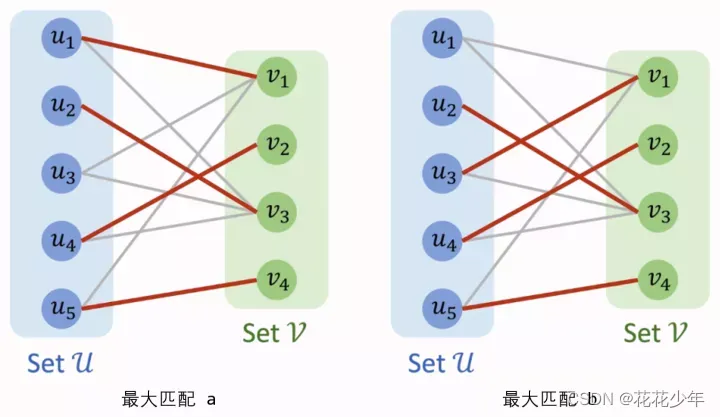
一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配（Maximum-Cardinality Matching）。最大匹配不唯一，如下图所示，下图的两个匹配都是最大匹配，最大匹配的边数为 4。
2.4 完美匹配
如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突），但并非每个图都存在完美匹配。
2.5 最大权匹配与最小权匹配
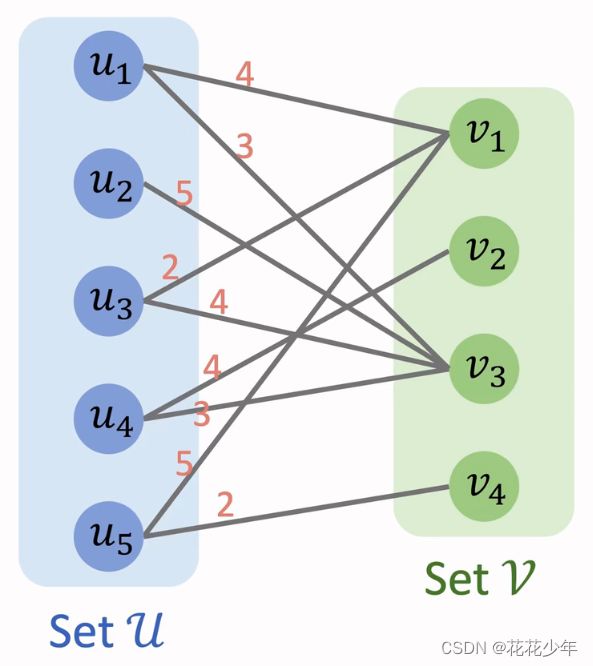
最大权匹配（Maximum-Weight Matching）表示的是有权图的所有匹配中边的权重之和最大的那些匹配，最小权匹配（Minimum-Weight Matching）表示的是有权图的所有匹配中边的权重之和最小的那些匹配。
对二分图所有的边赋上权重，将其转成有权二分图，如下图所示：
对于上面的有权二分图，我们将任意边上的权重记作 w \text{w} w，任意匹配记作 M \text{M} M，匹配 M \text{M} M 包含的所有匹配边的权重和记作函数 f ( M ) f(M) f(M)，则有权二分图的最大权匹配（Maximum-Weight Bipartite Matching）问题和有权二分图的最小权匹配（Minimum-Weight Bipartite Matching）问题可以用如下数学语言进行描述：
{ f ( M ) = ∑ ( u , v ) ∈ M w u , v max / min f ( M ) \left\{\begin{array}{l}f(M)=\sum_{(u,v)\in M}w_{u,v}\\\max/\min f(M)\end{array}\right. {f(M)=∑(u,v)∈Mwu,vmax/minf(M)
多目标跟踪数据关联问题可以转化为有权二分图最小权匹配问题，跟踪过程中的图像帧可以分别看作是有权二分图中的顶点集合 U \text U U 和 V \text V V，边的权重可以看作是前后帧目标之间的距离，通过某种方式计算得到的匹配距离（例如欧式距离），这个匹配距离称之为代价（Cost），所有的匹配距离构成了代价矩阵（Cost Matrix）。我们需要做的是，找到图像帧的匹配关系，使得总的匹配距离最小，代价最低。
3. 交替路径
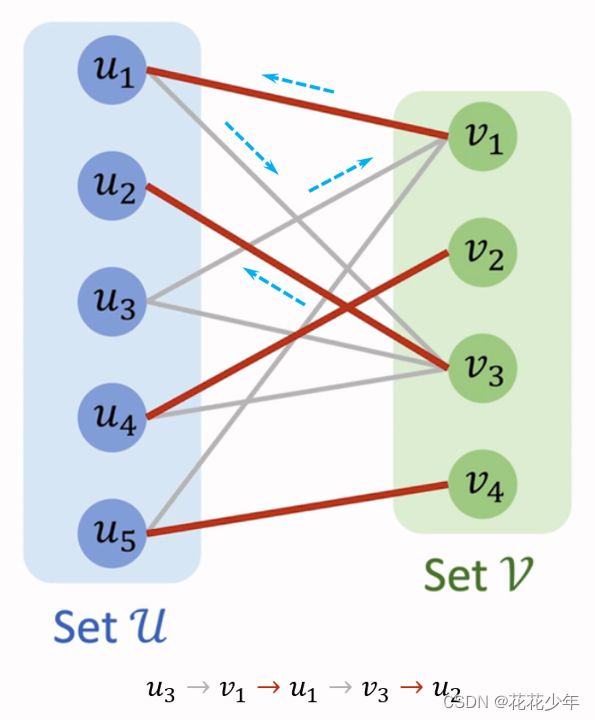
给定图 G = ( V , E ) G=(V,E) G=(V,E) 和它的一个匹配 M \text M M，交替路（Alternating Path）描述的是图中的这样一条路径：从图中的某个未匹配点出发，交替经过未匹配边和匹配边形成的路径。下面的二分图中，路径 u 3 → v 1 → u 1 → v 3 → u 2 u_3\to v_1\to u_1\to v_3\to u_2 u3→v1→u1→v3→u2 就是一条交替路：
4. 增广路径
4.1 增广路径的概念
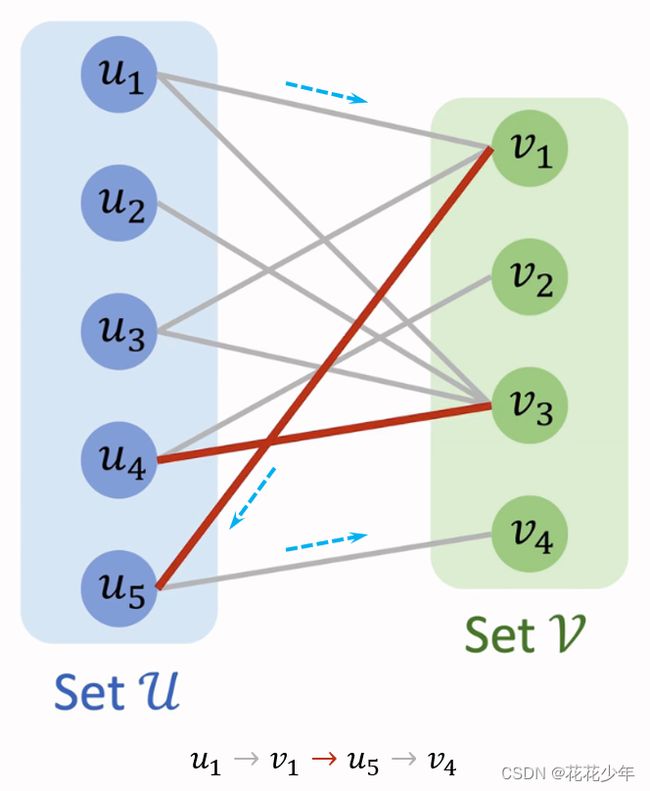
从图中的某个未匹配点起始，交替经过未匹配边和匹配边，并终止于不同于起始点的另一个未匹配点，则这条路径称为增广路径（Augmenting Path），增广路径是一条特殊的交替路。下面的二分图中，路径 u 1 → v 1 → u 5 → v 4 u_1\to v_1\to u_5\to v_4 u1→v1→u5→v4 就是一条增广路径。
4.2 增广路的性质
给定图 G = ( V , E ) G=(V,E) G=(V,E) 和它的一个匹配 M \text M M 以及增广路 P \text P P，并将 P \text P P 上所有的边记作集合 E P \text E_P EP，则有如下三个非常重要的性质：
-
Berge 定理：对于给定的图 G \text G G 和它的一个匹配 M \text M M， M \text M M 是 G \text G G 的最大匹配的充要条件是 G \text G G 中不存在匹配 M \text M M 的增广路；
-
E P \text E_P EP 中边的数量一定为奇数，且增广路 P \text P P 的第奇数条边不属于匹配 M \text M M，第偶数条边属于匹配 M \text M M，这意味着， E P \text E_P EP 中的未匹配边数量一定比匹配边数量多 1；
-
通过性质 1 不难发现，通过将 E P \text E_P EP 中的未匹配边取反变成匹配边，匹配边取反变成未匹配边，就可以多出 1 条匹配边，取反得到的新匹配边和 M \text M M 中不属于 E P \text E_P EP 的剩余边可以构成一个更大的匹配 M ′ M^{\prime} M′。在集合论中， M ′ M^{\prime} M′ 被称作 M \text M M 和 E P \text E_P EP 的对称差（Symmetric Difference），记作 M ⊖ E P M\ominus E_{P} M⊖EP：
M ⊖ E P = ( M ∪ E P ) − ( M ∩ E P ) M\ominus E_P=(M\cup E_P)-(M\cap E_P) M⊖EP=(M∪EP)−(M∩EP)
结合性质 1 和性质 3 我们不难发现，对于一个给定的二分图 G = ( U , V , E ) G=(U,V,E) G=(U,V,E) 和初始为空的匹配 M \text M M，我们只要反复搜索增广路就能逐渐扩展匹配的大小，最终当我们找不到增广路时就得到了一个最大匹配，下图中的示例很直观地展示了这个过程：
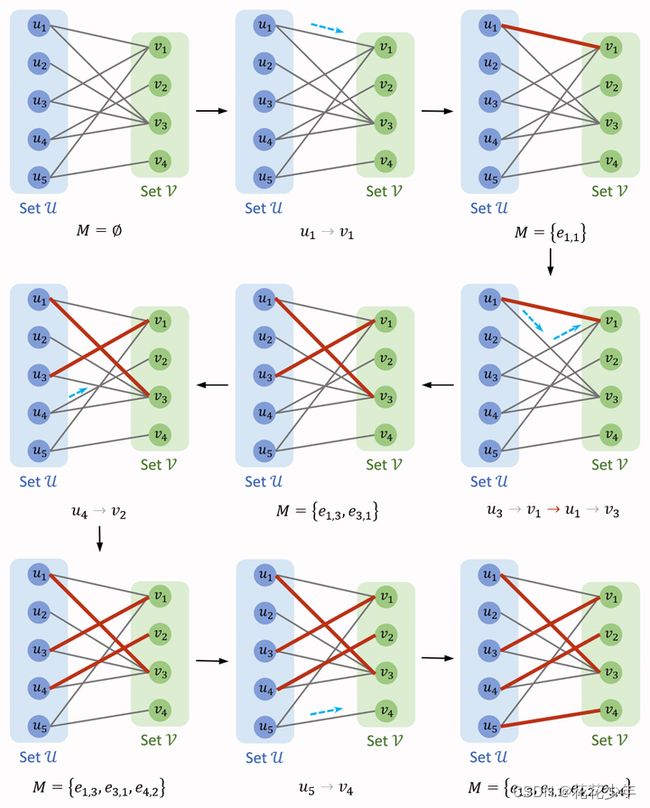
最后得到的 M = { e 1 , 3 , e 3 , 1 , e 4 , 2 , e 5 , 4 } M=\{e_{1,3},e_{3,1},e_{4,2},e_{5,4}\} M={e1,3,e3,1,e4,2,e5,4} 就是输入二分图 G \text G G 的一个最大匹配。
三、匈牙利算法
匈牙利算法（Hungarian algorithm），是由匈牙利数学家Edmonds于1965年提出，因而得名。匈牙利算法是全局最近邻（Global Nearest Neighbor，GNN）数据关联思想的一种具体实现，其最早用于求解经济学领域中的任务分配问题，后来发展成为图论领域中求解有权二分图最小权匹配问题的一般性算法。
匈牙利算法本质是图算法，该算法的核心就是寻找增广路径，它是一种利用增广路径求二分图最大匹配的算法，是一种能够在多项式时间内解决分配问题的组合优化算法。
1. 问题引入
在目标跟踪中，不同时刻物体的位置等信息发生变化，但我们需要让它保持同一个ID。
以目标跟踪小车为例，假设Frame1视频帧中出现一辆车，采用目标检测方法，可以一直把该黄车标成ID=1。
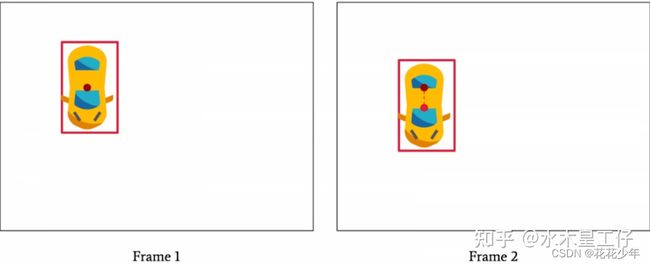
如果Frame2视频帧中出现了另外一台车，采用目标检测器只有分类出“车”的能力，无法知道黄车的ID是否等于1。
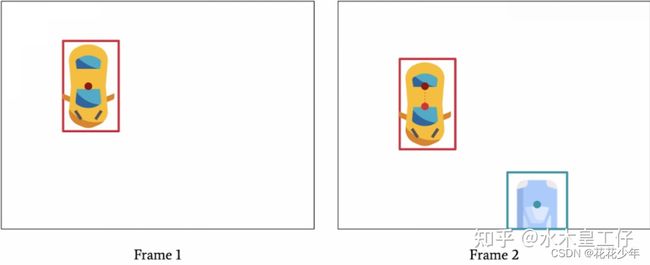
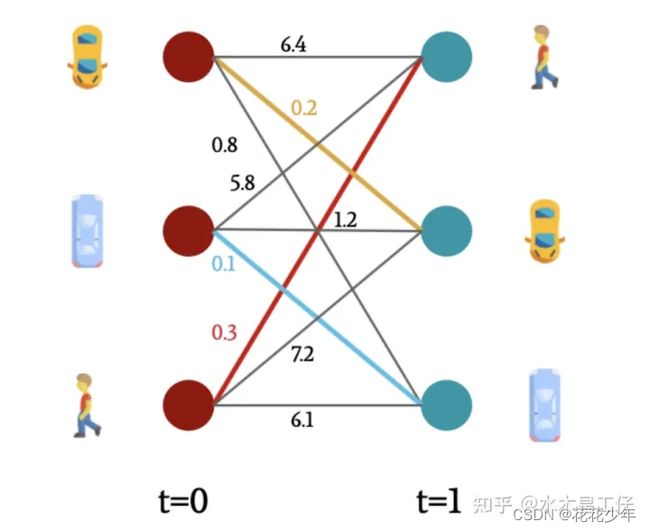
采用匈牙利算法，可以判断不同的ID。匈牙利算法会建立一个图，其中有当前帧t=1和前一帧t=0的节点，计算两帧节点之间的距离，距离越小，则当前帧的物体与前一帧物体相同的概率越大。
2. 适用场景
匈牙利算法多用于指派问题中，例如任务匹配问题。通过转化为二分图的形式，求解最大匹配，保证实现最优分配。
3. 匈牙利算法思想
**基本思想：**通过寻找增广路径，把增广路径中的匹配边和非匹配边的相互交换，这样就会多出一条匹配边，直到找不到增广路径为止。
以一个简单的例子，介绍匈牙利算法的思想。
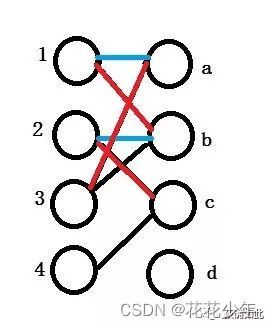
看这么一个例子，把左边1，2，3，4和右边a,b,c,d来进行匹配。
一开始我们给1分配a,1和a之间连上红线表示建立匹配。
然后接着给2分配b,2和b连上红线表示匹配。
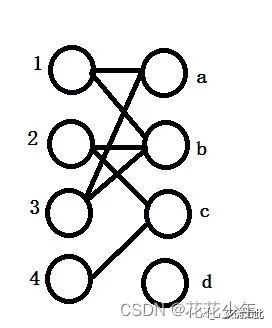
紧接着给3分配，这时候发现a,b已经都有所属了，我们尝试给1重新分配，把原来的分配拆掉，用蓝线表示。
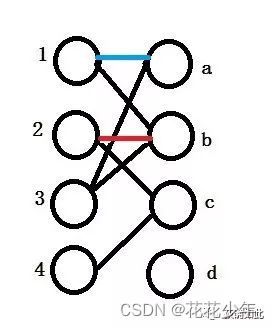
但是很快我们发现1重新分配不了，b已经有所属，那么继续尝试给2重新分配，把原来的分配拆掉，用蓝线表示。2重新分配到c，用红线表示。
这个时候，1可以重新分配到b,用红线表示。
最后，3就可以分配到a,用红线表示。
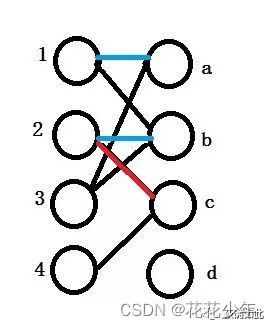
对于4，由于c已经被分配，而且尝试给其他1，2，3重新分配无法实现，就此结束。
总结：匈牙利算法的基本原则就是在原有匹配基础上重新分配，看是否可以添加一个新的匹配。
4. 匈牙利算法流程
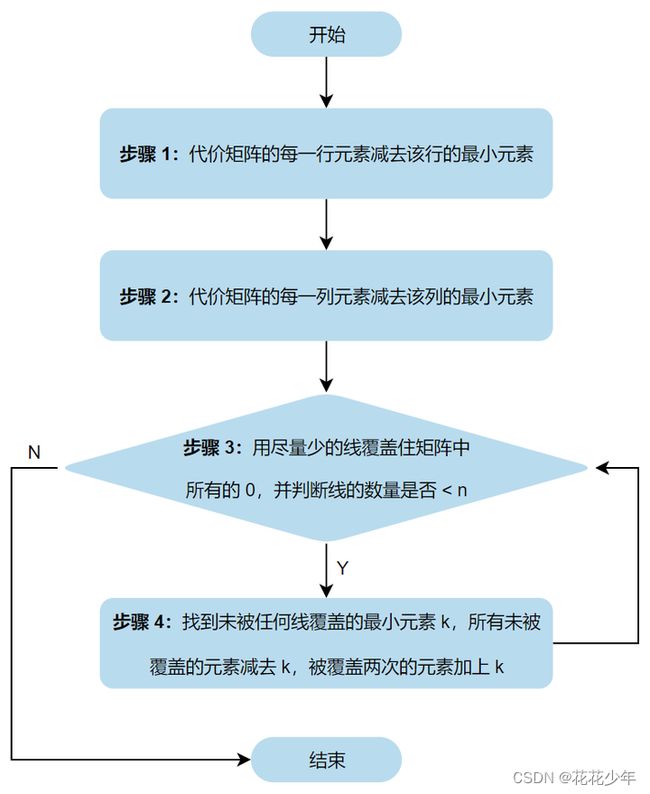
匈牙利算法就是用来解决分配问题（Assignment Problem），得到最优分配的结果。匈牙利算法的分配问题分 5 步工作：首先对矩阵进行缩减，然后交叉 0，最后再次缩减，直到我们可以对元素进行配对。总体流程如下：
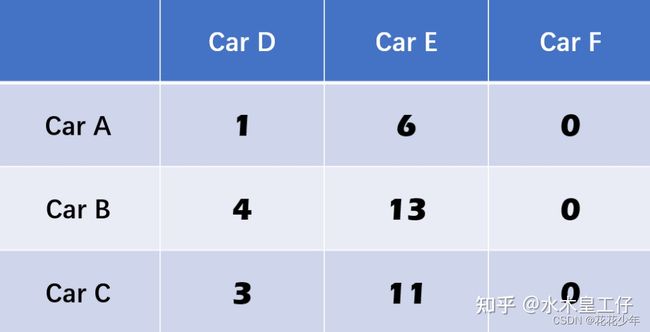
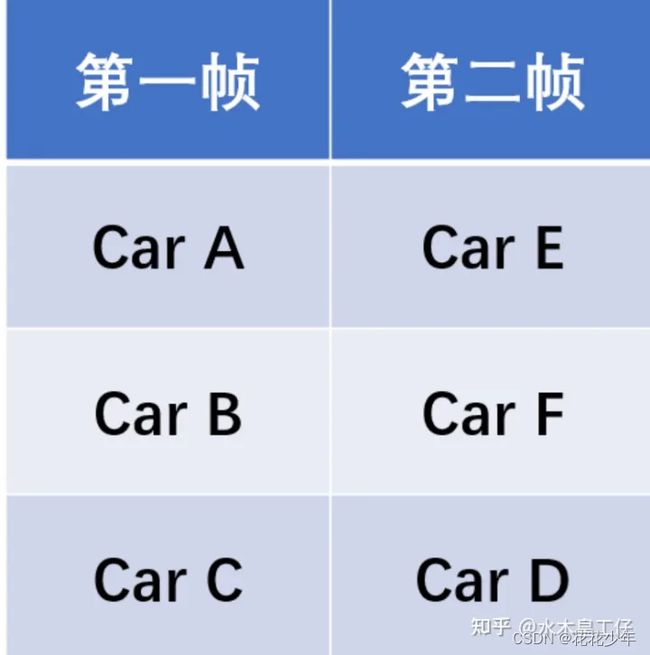
本章以一个抽象例子，介绍匈牙利算法解决分配问题的流程。假设我们有两帧图片，第一帧图片中有CarA, CarB, CarC, 并且通过目标检测器找到了这三辆车；第二帧，同样，也看到了三辆车，CarD, CarE, CarF，两帧都只存在这三辆车，但由于目标检测器只能分辨出他们是车，而不能分辨出CarD对应的是CarA还是其它车。可以测量出两帧之间车的对应距离，绘制出代价矩阵（cost matrix）。例如，第二帧的CarF与第一帧的CarA距离为9m，如下图数字所示。
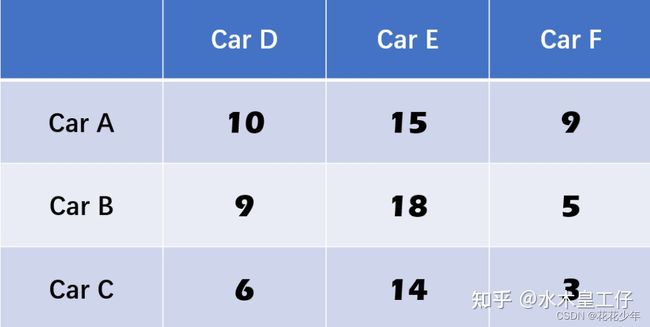
4.1 第一步：每行减去最小值
第一行最小的是9，则减去9，以此类推。最后变为：
4.2 第二步：每列减去最小值
第一列最小的是1，则减去1，以此类推。最后变为：
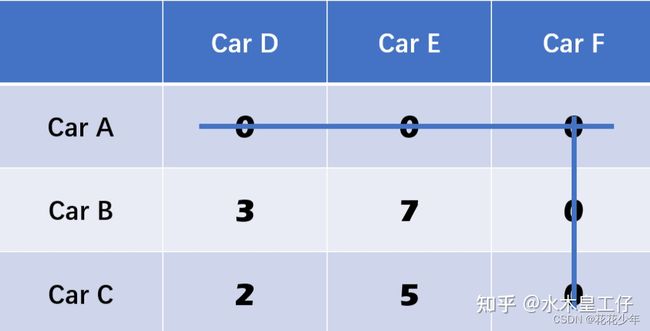
4.3 第三步：以最少数量的线条划掉所有零
划掉所有零有不少方式，如下图：
但明显最少的方式应该是两条：
如果这个数量大于等于矩阵的行列数，那么跳到第五步。
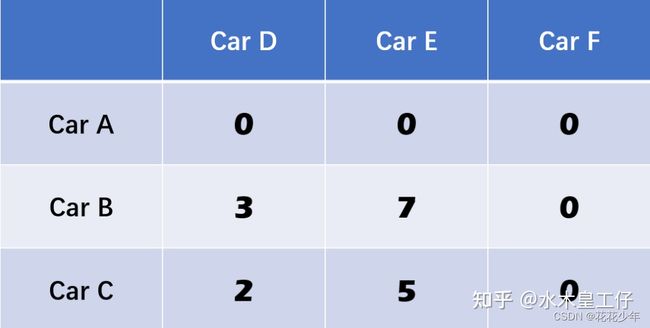
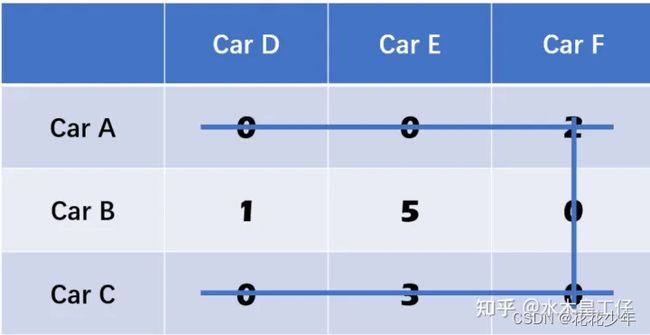
4.4 第四步：在剩下的矩阵中，减去最小值
在剩下的矩阵中，减去最小值；如果有零被交叉，那么把这个最小值加上去。
剩下的矩阵为【【3， 7】，【2， 5】】，都减去2。然后右叉的0加上2。变为：
然后重复第三步，最后变为：
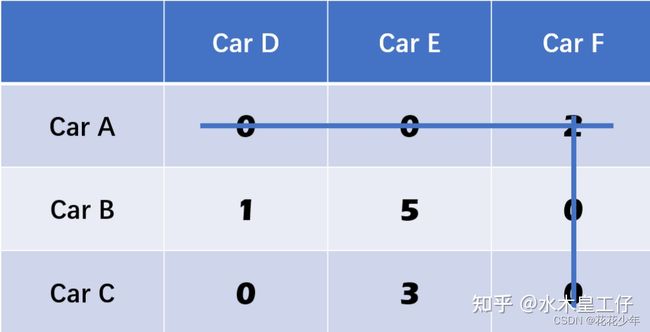
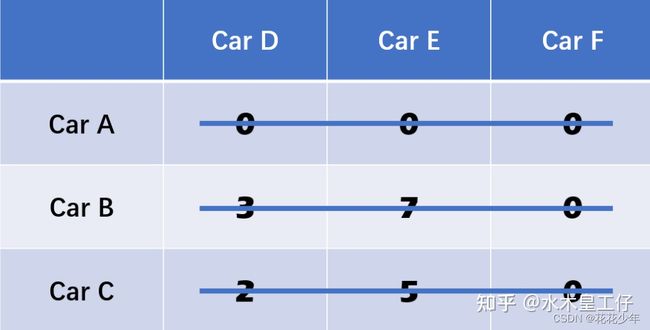
这时我们有3条线了，那么跳到第五步。
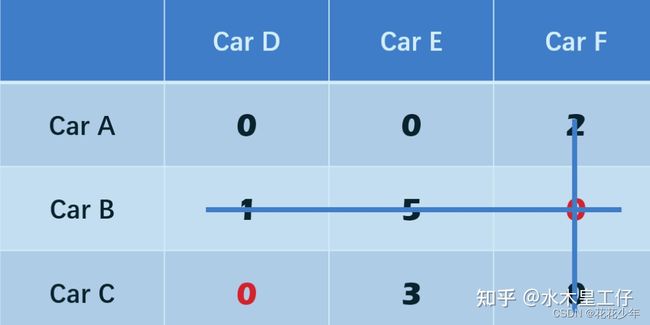
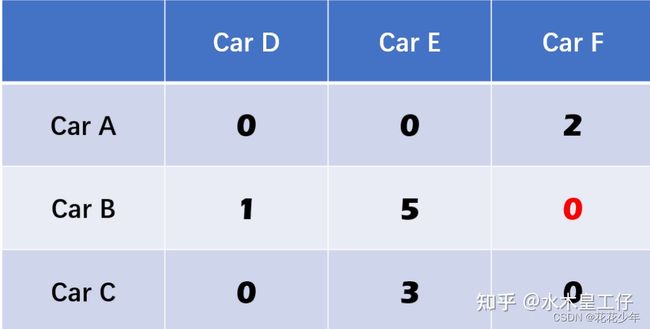
4.5 第五步：从只有一个零的行开始一一对应，对应完则整个行列删除
第二行只有一个零，那么Car F 对应了car B，然后删掉行列。最后变为：
第三行，Car C对应了Car D。
剩下就是Car A对应Car E了。最终结果为：
5. Python实现匈牙利算法
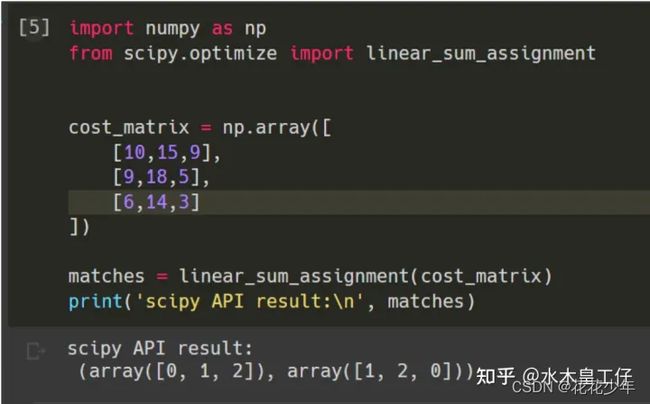
scipy的库linear_sum_assignment
sklearn里的 linear_assignment() 函数以及scipy里的 linear_sum_assignment() 函数都实现了匈牙利算法，两者的返回值的形式不同：
import numpy as np
from sklearn.utils.linear_assignment_ import linear_assignment
from scipy.optimize import linear_sum_assignment
cost_matrix = np.array([
[10,15,9],
[9,18,5],
[6,14,3]
])
matches = linear_assignment(cost_matrix)
print('sklearn API result:\n', matches)
matches = linear_sum_assignment(cost_matrix)
print('scipy API result:\n', matches)
"""Outputs
sklearn API result:
[[0 1]
[1 2]
[2 0]]
scipy API result:
(array([0, 1, 2], dtype=int64), array([1, 2, 0], dtype=int64))
"""
可以看到，他直接帮你匹配好了，0(Car A) → 1(Car E)。
6. 匈牙利算法特例
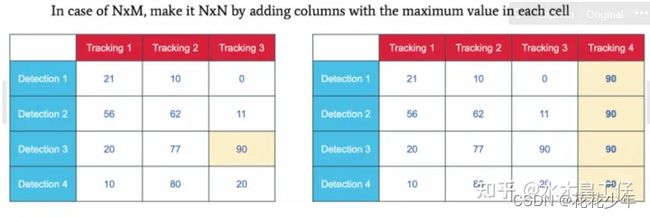
NxN vs NxM
如果有 NxM 矩阵，则可以通过添加具有最大值的列来使其成为 NxN 矩阵。
刚刚我们的矩阵的行列数是相等的，那是因为两帧的图片都只出现了三辆车，那么如果第一帧三辆车，第二帧出现了四辆车呢？ 如果出现这种情况，我们只需要添加一个新的边缘给我们的图标，这个值是我们原先的最大值就可以了。
最大值 vs 最小值
如果我们使用IOU匹配的话，我们需要优化的是最大值。我们只需要在第一步进行一个转换，如下所示：
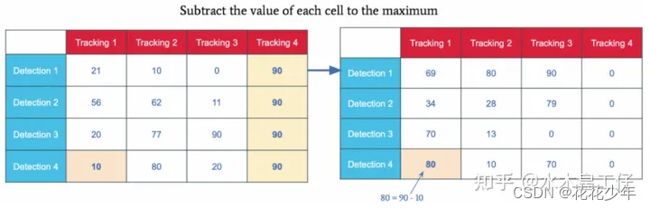
例如，在Detenction 4, Tracking 1中（行4列1），cost metric 只有10，如果是IOU匹配的话，表示这个匹配度很低，我们把所有的值都让最大值减去这个值，比如10，我们让90 - 10 = 80。
四、目标跟踪算法
目前主流的目标跟踪算法，都是基于Tracking-by-Detection策略，即基于目标检测的结果来进行目标跟踪。DeepSort就是运用这个策略。
视频中不同时刻的同一个人，位置发生了变化，如何关联上呢？答案就是匈牙利算法和卡尔曼滤波。
- 匈牙利算法：匹配当前帧的某个目标与前一帧的某个目标；
- 卡尔曼滤波：基于目标前一时刻的位置，来预测当前时刻的位置，可以比目标检测器更准确的估计目标的位置。
1. 目标框的距离计算
目前经典的MOT多目标跟踪算法是sort、deepsort，其中sort算法是先经过匈牙利算法进行最大匹配，再经过卡尔曼滤波进行预测。
在实际的目标跟踪当中，我们获取前一帧的跟踪框track 和当前帧的检测框detection ，之间的距离Cost Metric 如何计算的呢？
检测框则是当前帧的目标检测器检测出来的bounding box, 跟踪框是上一帧最后输出预测出来的框，并不是检测框。
目标框的距离计算，常用有三种方法：欧式距离，IOU匹配，外观相似度（Convolutional Cost）。
1.1 欧式距离
我们可以把两帧的目标框的中心点进行一个距离的计算：
d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 \mathrm{d}=\sqrt{(x_2-x_1)_2+(y_2-y_1)^2} d=(x2−x1)2+(y2−y1)2
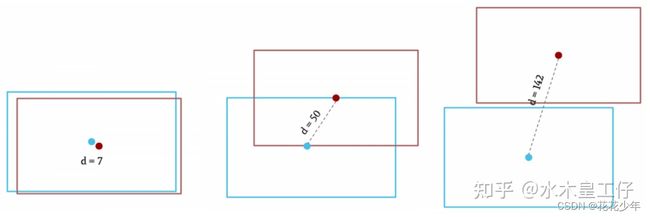
这种方法最简单，但如果目标的形状发生变化，或者目标与其他发生了重叠，会有不少问题。
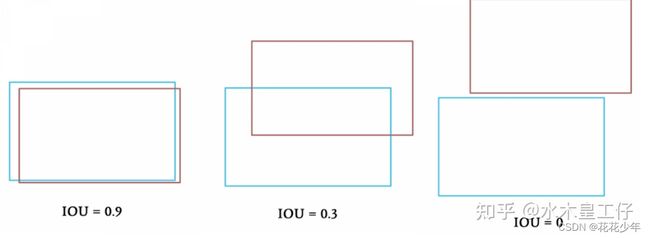
1.2 IOU匹配
由图可知，这种方法有个问题，就是我们现在不是求最小，而是求最大，所以会与上述说的方法有一些出入。
1.3 外观相似度（Convolutional Cost）
IOU匹配是很常用的，但是如果出现了目标的重叠阻挡等问题，目标框也会发生变化，IOU匹配也会不准确。
但即使目标有遮挡，但如果我们一样能检测其中一部分，那么我们能不能用一个卷积网络提取其中的特征，然后和原本的框的特征进行相比呢？如下图：
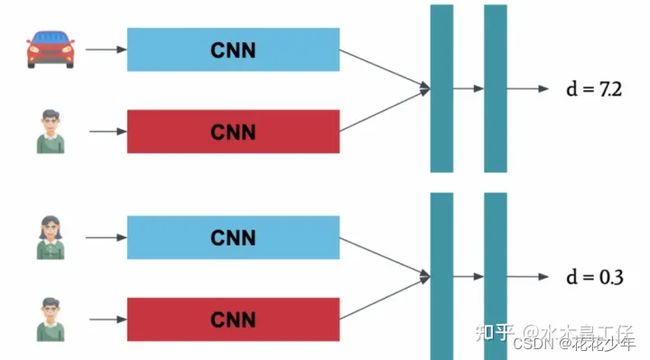
加入了外观信息，借用ReID领域模型来提取特征，减少了ID switch，这也是DeepSort相比Sort的其中一个创新点。
五、DeepSort算法
目标跟踪初探（DeepSORT）
deep_sort_pytorch
1. DeepSort算法简介
在DeepSort算法中，匈牙利算法用来将前一帧中的跟踪框tracks与当前帧中的检测框detections进行关联匹配，通过外观信息（appearance information）和欧式距离或者IOU来计算代价矩阵。
源码解读
# linear_assignment.py
def min_cost_matching(distance_metric, max_distance, tracks, detections,
track_indices=None, detection_indices=None):
...
# 计算代价矩阵
cost_matrix = distance_metric(tracks, detections, track_indices, detection_indices)
cost_matrix[cost_matrix > max_distance] = max_distance + 1e-5
# 执行匈牙利算法，得到匹配成功的索引对，行索引为tracks的索引，列索引为detections的索引
row_indices, col_indices = linear_assignment(cost_matrix)
matches, unmatched_tracks, unmatched_detections = [], [], []
# 找出未匹配的detections
for col, detection_idx in enumerate(detection_indices):
if col not in col_indices:
unmatched_detections.append(detection_idx)
# 找出未匹配的tracks
for row, track_idx in enumerate(track_indices):
if row not in row_indices:
unmatched_tracks.append(track_idx)
# 遍历匹配的(track, detection)索引对
for row, col in zip(row_indices, col_indices):
track_idx = track_indices[row]
detection_idx = detection_indices[col]
# 如果相应的cost大于阈值max_distance，也视为未匹配成功
if cost_matrix[row, col] > max_distance:
unmatched_tracks.append(track_idx)
unmatched_detections.append(detection_idx)
else:
matches.append((track_idx, detection_idx))
return matches, unmatched_tracks, unmatched_detections
2. DeepSort算法流程
DeepSORT对每一帧的处理流程如下：
检测器得到bbox → 生成detections → 卡尔曼滤波预测→ 使用匈牙利算法将预测后的tracks和当前帧中的detecions进行匹配（级联匹配和IOU匹配） → 卡尔曼滤波更新。
**Frame 0：**检测器检测到了3个detections，当前没有任何tracks，将这3个detections初始化为tracks。
**Frame 1：**检测器又检测到了3个detections，对于Frame 0中的tracks，先进行预测得到新的tracks，然后使用匈牙利算法将新的tracks与detections进行匹配，得到(track, detection)匹配对，最后用每对中的detection更新对应的track。
2.1 检测器得到bbox
使用Yolo作为检测器，检测当前帧中的bbox：
# demo_yolo3_deepsort.py
def detect(self):
while self.vdo.grab():
...
bbox_xcycwh, cls_conf, cls_ids = self.yolo3(im) # 检测到的bbox[cx,cy,w,h]，置信度，类别id
if bbox_xcycwh is not None:
# 筛选出人的类别
mask = cls_ids == 0
bbox_xcycwh = bbox_xcycwh[mask]
bbox_xcycwh[:, 3:] *= 1.2
cls_conf = cls_conf[mask]
...
2.2 生成detections
将检测到的bbox转换成detections：
# deep_sort.py
def update(self, bbox_xywh, confidences, ori_img):
self.height, self.width = ori_img.shape[:2]
# 提取每个bbox的feature
features = self._get_features(bbox_xywh, ori_img)
# [cx,cy,w,h] -> [x1,y1,w,h]
bbox_tlwh = self._xywh_to_tlwh(bbox_xywh)
# 过滤掉置信度小于self.min_confidence的bbox，生成detections
detections = [Detection(bbox_tlwh[i], conf, features[i]) for i,conf in enumerate(confidences) if conf > self.min_confidence]
# NMS (这里self.nms_max_overlap的值为1，即保留了所有的detections)
boxes = np.array([d.tlwh for d in detections])
scores = np.array([d.confidence for d in detections])
indices = non_max_suppression(boxes, self.nms_max_overlap, scores)
detections = [detections[i] for i in indices]
...
2.3 卡尔曼滤波预测tracks
使用卡尔曼滤波预测前一帧中的tracks在当前帧的状态：
# track.py
def predict(self, kf):
"""Propagate the state distribution to the current time step using a
Kalman filter prediction step.
Parameters
----------
kf: The Kalman filter.
"""
self.mean, self.covariance = kf.predict(self.mean, self.covariance) # 预测
self.age += 1 # 该track自出现以来的总帧数加1
self.time_since_update += 1 # 该track自最近一次更新以来的总帧数加1
2.4 匈牙利算法关联匹配
首先对基于外观信息的欧式距离计算tracks和detections的代价矩阵，然后相继进行级联匹配和IOU匹配，最后得到当前帧的所有匹配对、未匹配的tracks以及未匹配的detections：
# tracker.py
def _match(self, detections):
def gated_metric(racks, dets, track_indices, detection_indices):
"""
基于外观信息和欧式距离，计算卡尔曼滤波预测的tracks和当前时刻检测到的detections的代价矩阵
"""
features = np.array([dets[i].feature for i in detection_indices])
targets = np.array([tracks[i].track_id for i in track_indices]
# 基于外观信息，计算tracks和detections的余弦距离代价矩阵
cost_matrix = self.metric.distance(features, targets)
# 基于欧式距离，过滤掉代价矩阵中一些不合适的项 (将其设置为一个较大的值)
cost_matrix = linear_assignment.gate_cost_matrix(self.kf, cost_matrix, tracks,
dets, track_indices, detection_indices)
return cost_matrix
# 区分开confirmed tracks和unconfirmed tracks
confirmed_tracks = [i for i, t in enumerate(self.tracks) if t.is_confirmed()]
unconfirmed_tracks = [i for i, t in enumerate(self.tracks) if not t.is_confirmed()]
# 对confirmd tracks进行级联匹配
matches_a, unmatched_tracks_a, unmatched_detections = \
linear_assignment.matching_cascade(
gated_metric, self.metric.matching_threshold, self.max_age,
self.tracks, detections, confirmed_tracks)
# 对级联匹配中未匹配的tracks和unconfirmed tracks中time_since_update为1的tracks进行IOU匹配
iou_track_candidates = unconfirmed_tracks + [k for k in unmatched_tracks_a if
self.tracks[k].time_since_update == 1]
unmatched_tracks_a = [k for k in unmatched_tracks_a if
self.tracks[k].time_since_update != 1]
matches_b, unmatched_tracks_b, unmatched_detections = \
linear_assignment.min_cost_matching(
iou_matching.iou_cost, self.max_iou_distance, self.tracks,
detections, iou_track_candidates, unmatched_detections)
# 整合所有的匹配对和未匹配的tracks
matches = matches_a + matches_b
unmatched_tracks = list(set(unmatched_tracks_a + unmatched_tracks_b))
return matches, unmatched_tracks, unmatched_detections
# 级联匹配源码 linear_assignment.py
def matching_cascade(distance_metric, max_distance, cascade_depth, tracks, detections,
track_indices=None, detection_indices=None):
...
unmatched_detections = detection_indice
matches = []
# 由小到大依次对每个level的tracks做匹配
for level in range(cascade_depth):
# 如果没有detections，退出循环
if len(unmatched_detections) == 0:
break
# 当前level的所有tracks索引
track_indices_l = [k for k in track_indices if
tracks[k].time_since_update == 1 + level]
# 如果当前level没有track，继续
if len(track_indices_l) == 0:
continue
# 匈牙利匹配
matches_l, _, unmatched_detections = min_cost_matching(distance_metric, max_distance, tracks, detections,
track_indices_l, unmatched_detections)
matches += matches_l
unmatched_tracks = list(set(track_indices) - set(k for k, _ in matches))
return matches, unmatched_tracks, unmatched_detections
2.5 卡尔曼滤波更新
对于每个匹配成功的track，用其对应的detection进行更新，并处理未匹配tracks和detections：
# tracker.py
def update(self, detections):
"""Perform measurement update and track management.
Parameters
----------
detections: List[deep_sort.detection.Detection]
A list of detections at the current time step.
"""
# 得到匹配对、未匹配的tracks、未匹配的dectections
matches, unmatched_tracks, unmatched_detections = self._match(detections)
# 对于每个匹配成功的track，用其对应的detection进行更新
for track_idx, detection_idx in matches:
self.tracks[track_idx].update(self.kf, detections[detection_idx])
# 对于未匹配的成功的track，将其标记为丢失
for track_idx in unmatched_tracks:
self.tracks[track_idx].mark_missed()
# 对于未匹配成功的detection，初始化为新的track
for detection_idx in unmatched_detections:
self._initiate_track(detections[detection_idx])
...