动手学深度学习-pytorch版本(二):线性神经网络
参考引用
- 动手学深度学习
1. 线性神经网络
- 神经网络的整个训练过程,包括: 定义简单的神经网络架构、数据处理、指定损失函数和如何训练模型。经典统计学习技术中的线性回归和 softmax 回归可以视为线性神经网络
1.1 线性回归
- 回归 (regression) 是能为一个或多个自变量与因变量之间关系建模的一类方法。在自然科学和社会科学领域,回归经常用来表示输入和输出之间的关系
- 在机器学习领域中的大多数任务通常都与预测 (prediction) 有关。当想预测一个数值时,就会涉及到回归问题。常见的例子包括:预测价格 (房屋、股票等)、预测住院时间 (针对住院病人等)、预测需求 (零售销量等)
1.1.1 线性回归的基本元素
-
线性回归基于几个简单的假设
- 首先,假设自变量 x x x 和因变量 y y y 之间的关系是线性的,即 y y y 可以表示为 x x x 中元素的加权和
- 其次,通常允许包含观测值的一些噪声,并假设任何噪声都比较正常,如噪声遵循正态分布
-
举一个实际的例子:希望根据房屋的面积 (平方英尺) 和房龄 (年) 来估算房屋价格 (美元)
- 为了开发一个能预测房价的模型,需要收集一个真实的数据集
- 这个数据集包括了房屋的销售价格、面积和房龄
- 在机器学习的术语中,该数据集称为训练集 (training set)
- 每行数据 (比如一次房屋交易相对应的数据) 称为样本 (sample),也可以称为数据点 (data point) 或数据样本 (data instance)
- 把试图预测的目标 (比如预测房屋价格) 称为标签 (label) 或目标 (target)
- 预测所依据的自变量 (面积和房龄) 称为特征 (feature) 或协变量 (covariate)
- 为了开发一个能预测房价的模型,需要收集一个真实的数据集
线性模型
-
线性假设是指:目标 (房屋价格) 可以表示为特征 (面积和房龄) 的加权和
p r i c e = w a r e a ⋅ a r e a + w a g e ⋅ a g e + b \mathrm{price}=w_{\mathrm{area}}\cdot\mathrm{area}+w_{\mathrm{age}}\cdot\mathrm{age}+b price=warea⋅area+wage⋅age+b- w a r e a w_{area} warea 和 w a g e w_{age} wage 称为权重 (weight),权重决定了每个特征对预测值的影响
- b b b 称为偏置 (bias)、偏移量 (offset) 或截距 (intercept)。偏置是指当所有特征都取 0 时,预测值应该为多少。如果没有偏置项,模型的表达能力将受到限制
- 上式是输入特征的一个仿射变换 (affine transformation)。仿射变换是通过加权和对特征进行线性变换,并通过偏置项来平移
-
给定一个数据集,目标是寻找模型的权重 w w w 和偏置 b b b,使得根据模型做出的预测大体符合数据里的真实价格。输出的预测值由输入特征通过线性模型的仿射变换决定,仿射变换由所选权重和偏置确定
-
而在机器学习领域,通常使用高维数据集,当输入包含 d d d 个特征时,预测结果 y ^ \hat{y} y^ (使用 “尖角” 符号表示 y y y 的估计值) 表示为
y ^ = w 1 x 1 + . . . + w d x d + b \hat{y}=w_1x_1+...+w_dx_d+b y^=w1x1+...+wdxd+b -
将所有特征放到向量 x ∈ R d {\mathbf{x}}\in\mathbb{R}^{d} x∈Rd 中,并将所有权重放到向量 w ∈ R d {\mathbf{w}}\in\mathbb{R}^{d} w∈Rd 中,可以用点积形式来简洁地表达模型
y ^ = w ⊤ x + b \hat{y}=\mathbf{w}^\top\mathbf{x}+b y^=w⊤x+b -
上式中,向量 x {\mathbf{x}} x 对应于单个数据样本的特征。用符号表示的矩阵 X ∈ R n × d \mathbf{X}\in\mathbb{R}^{n\times d} X∈Rn×d 可以很方便地引用整个数据集的 n n n 个样本。其中, X \mathbf{X} X 的每一行是一个样本,每一列是一种特征。对于特征集合 X \mathbf{X} X,预测值 y ^ ∈ R n \hat{\mathbf{y}}\in\mathbb{R}^{n} y^∈Rn 可以通过矩阵-向量乘法表示为
y ^ = X w + b \hat{\mathbf{y}}=\mathbf{X}\mathbf{w}+b y^=Xw+b -
给定训练数据特征 X \mathbf{X} X 和对应的已知标签 y y y,线性回归的目标是找到一组权重向量 w w w 和偏置 b b b
- 当给定从 X \mathbf{X} X 的同分布中取样的新样本特征时,这组权重向量和偏置能够使得新样本预测标签的误差尽可能小
- 即使确信特征与标签的潜在关系是线性的,也会加入一个噪声项来考虑观测误差带来的影响
在开始寻找最好的模型参数 (model parameters) w w w 和 b b b 之前,还需要两个东西
- (1) 一种模型质量的度量方式
- (2) 一种能够更新模型以提高模型预测质量的方法
损失函数
-
在考虑如何用模型拟合数据之前,需要确定一个拟合程度的度量。损失函数 (loss function) 能够量化目标的实际值与预测值之间的差距。通常选择非负数作为损失,且数值越小表示损失越小,完美预测时的损失为 0。回归问题中最常用的损失函数是平方误差函数。当样本 i i i 的预测值为 y ^ ( i ) \hat{y}^{(i)} y^(i),其相应的真实标签为 y ( i ) y^{(i)} y(i) 时,平方误差可以定义为以下公式
l ( i ) ( w , b ) = 1 2 ( y ^ ( i ) − y ( i ) ) 2 l^{(i)}(\mathbf{w},b)=\frac12\left(\hat{y}^{(i)}-y^{(i)}\right)^2 l(i)(w,b)=21(y^(i)−y(i))2 -
由于平方误差函数中的二次方项,估计值 y ^ ( i ) \hat{y}^{(i)} y^(i) 和观测值 y ( i ) y^{(i)} y(i) 之间较大的差异将导致更大的损失。为了度景模型在整个数据集上的质量,需计算在训练集 n n n 个样本上的损失均值 (也等价于求和)
L ( w , b ) = 1 n ∑ i = 1 n l ( i ) ( w , b ) = 1 n ∑ i = 1 n 1 2 ( w ⊤ x ( i ) + b − y ( i ) ) 2 L(\mathbf{w},b)=\frac1n\sum_{i=1}^nl^{(i)}(\mathbf{w},b)=\frac1n\sum_{i=1}^n\frac12\left(\mathbf{w}^\top\mathbf{x}^{(i)}+b-y^{(i)}\right)^2 L(w,b)=n1i=1∑nl(i)(w,b)=n1i=1∑n21(w⊤x(i)+b−y(i))2 -
在训练模型时,希望寻找一组参数 ( w ∗ , b ∗ ) (\mathbf{w}^*,b^*) (w∗,b∗),这组参数能最小化在所有训练样本上的总损失
w ∗ , b ∗ = argmin w , b L ( w , b ) \mathbf{w}^*,b^*=\underset{\mathbf{w},b}{\operatorname*{argmin}}L(\mathbf{w},b) w∗,b∗=w,bargminL(w,b)
解析解
- 与其他大部分模型不同,线性回归的解可以用一个公式简单地表达出来,这类解叫作解析解。首先,将偏置 b b b 合并到参数 w \mathbf{w} w 中,合并方法是在包含所有参数的矩阵中附加一列。预测问题是最小化 ∥ y − X w ∥ 2 \|\mathbf{y}-\mathbf{X}\mathbf{w}\|^2 ∥y−Xw∥2。这在损失平面上只有一个临界点,这个临界点对应于整个区域的损失极小点。将损失关于 w \mathbf{w} w 的导数设为 0,得到解析解
w ∗ = ( X ⊤ X ) − 1 X ⊤ y \mathbf{w}^*=(\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{X}^\top\mathbf{y} w∗=(X⊤X)−1X⊤y
随机梯度下降
-
梯度下降 (gradient descent) 的方法几乎可以优化所有深度学习模型,它通过不断地在损失函数递减的方向上更新参数来降低误差
-
通常在每次需要计算更新的时候随机抽取一小批样本,这叫做小批量随机梯度下降(minibatch stochastic gradient descent)
- 在每次迭代中,首先随机抽样一个小批量 B \mathcal{B} B,它是由固定数量的训练样本组成的
- 然后,计算小批量的平均损失关于模型参数的导数 (也可以称为梯度)
- 最后,将梯度乘以一个预先确定的正数 η \eta η,并从当前参数的值中减掉
w ← w − η ∣ B ∣ ∑ i ∈ B ∂ w l ( i ) ( w , b ) = w − η ∣ B ∣ ∑ i ∈ B x ( i ) ( w ⊤ x ( i ) + b − y ( i ) ) , b ← b − η ∣ B ∣ ∑ i ∈ B ∂ b l ( i ) ( w , b ) = b − η ∣ B ∣ ∑ i ∈ B ( w ⊤ x ( i ) + b − y ( i ) ) . \begin{aligned}\mathbf{w}&\leftarrow\mathbf{w}-\frac\eta{|\mathcal{B}|}\sum_{i\in\mathcal{B}}\partial_\mathbf{w}l^{(i)}(\mathbf{w},b)=\mathbf{w}-\frac\eta{|\mathcal{B}|}\sum_{i\in\mathcal{B}}\mathbf{x}^{(i)}\left(\mathbf{w}^\top\mathbf{x}^{(i)}+b-y^{(i)}\right),\\b&\leftarrow b-\frac\eta{|\mathcal{B}|}\sum_{i\in\mathcal{B}}\partial_bl^{(i)}(\mathbf{w},b)=b-\frac\eta{|\mathcal{B}|}\sum_{i\in\mathcal{B}}\left(\mathbf{w}^\top\mathbf{x}^{(i)}+b-y^{(i)}\right).\end{aligned} wb←w−∣B∣ηi∈B∑∂wl(i)(w,b)=w−∣B∣ηi∈B∑x(i)(w⊤x(i)+b−y(i)),←b−∣B∣ηi∈B∑∂bl(i)(w,b)=b−∣B∣ηi∈B∑(w⊤x(i)+b−y(i)).
-
B \mathcal{B} B 表示每个小批量中的样本数,这也称为批量大小 (batch size)。 η \eta η 表示学习率 (learning rate)。批量大小和学习率的值通常是手动预先指定,而不是通过模型训练得到的
- 这些可调整但不在训练过程中更新的参数称为超参数 (hyperparameter)。调参 (hyperparameter tuning) 是选择超参数的过程
- 超参数通常是根据训练迭代结果来调整的,而训练迭代结果是在独立的验证数据集 上评估得到的
用模型进行预测
- 给定 “已学习” 的线性回归模型 w ^ ⊤ x + b ^ \mathbf{\hat{w}}^{\top}\mathbf{x}+\hat{b} w^⊤x+b^,现在可以通过房屋面积 x 1 x_1 x1 和房龄 x 2 x_2 x2 来估计一个 (末包含在训练数据中的) 新房屋价格。给定特征估计目标的过程通常称为预测 (prediction) 或推断 (inference)
1.1.2 矢量化加速
- 在训练模型时,经常希望能够同时处理整个小批量的样本,为实现这一点,需要对计算进行矢量化
- 为说明矢量化的重要性,考虑对向量相加的两种方法,实例化两个全为 1 的 10000 维向量
- 在一种方法中,使用 Python 的 for 循环遍历向量
- 在另一种方法中,依赖对 + 的调用
import math import time import numpy as np import torch n = 10000 a = torch.ones([n]) b = torch.ones([n]) # 定义一个计时器 class Timer: def __init__(self): self.times = [] self.start() def start(self): self.tik = time.time() def stop(self): self.times.append(time.time() - self.tik) return self.times[-1] def avg(self): return sum(self.times) / len(self.times) def sum(self): return sum(self.times) def cumsum(self): return np.array(self.times).cumsum().tolist() # 使用 for 循环,每次执行一位的加法 c = torch.zeros(n) timer = Timer() for i in range(n): c[i] = a[i] + b[i] # 使用重载的 + 运算符来计算按元素的和 # 矢量化代码通常会带来数量级的加速 timer.start() d = a + b print(f'{timer.stop():.5f} sec')# 输出 '0.20727 sec' '0.00020 sec'
1.1.3 正态分布与平方损失
-
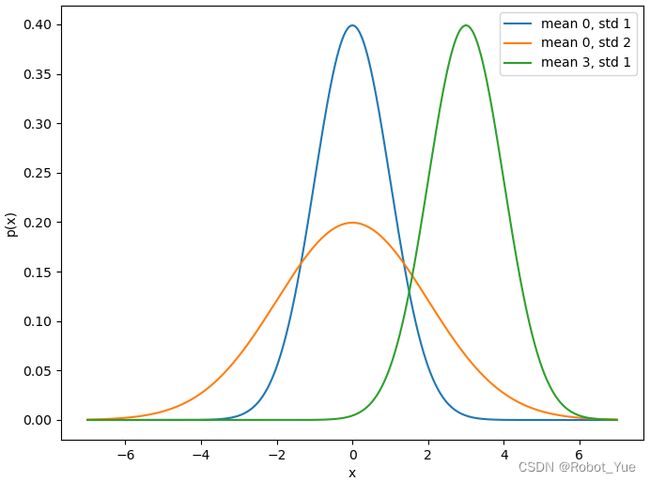
通过对噪声分布的假设来解读平方损失目标函数。正态分布 (normal distribution),也称为高斯分布 (Gaussian distribution):若随机变量 x x x 具有均值 μ \mu μ 和方差 σ 2 \sigma^{2} σ2 (标准差 σ \sigma σ),其正态分布概率密度函数如下
p ( x ) = 1 2 π σ 2 exp ( − 1 2 σ 2 ( x − μ ) 2 ) \begin{aligned}p(x)&=\frac1{\sqrt{2\pi\sigma^2}}\exp\left(-\frac1{2\sigma^2}(x-\mu)^2\right)\end{aligned} p(x)=2πσ21exp(−2σ21(x−μ)2) -
均方误差损失函数 (简称均方损失) 可以用于线性回归的一个原因是:假设了观测中包含噪声,其中噪声服从正态分布。噪声正态分布如下式,其中 ϵ ∼ N ( 0 , σ 2 ) \epsilon\sim\mathcal{N}(0,\sigma^2) ϵ∼N(0,σ2)
y = w ⊤ x + b + ϵ y=\mathbf{w}^\top\mathbf{x}+b+\epsilon y=w⊤x+b+ϵ -
因此,现在可以写出通过给定的 x \mathbf{x} x 观测到特定 y y y 的似然 (likelihood)
P ( y ∣ x ) = 1 2 π σ 2 exp ( − 1 2 σ 2 ( y − w ⊤ x − b ) 2 ) P(y\mid\mathbf{x})=\frac1{\sqrt{2\pi\sigma^2}}\exp\left(-\frac1{2\sigma^2}(y-\mathbf{w}^\top\mathbf{x}-b)^2\right) P(y∣x)=2πσ21exp(−2σ21(y−w⊤x−b)2) -
现在,根据极大似然估计法,参数 w \mathbf{w} w 和 b b b 的最优值是使整个数据集的似然最大的值
P ( y ∣ X ) = ∏ i = 1 n p ( y ( i ) ∣ x ( i ) ) P(\mathbf{y}\mid\mathbf{X})=\prod_{i=1}^np(y^{(i)}|\mathbf{x}^{(i)}) P(y∣X)=i=1∏np(y(i)∣x(i))
− log P ( y ∣ X ) = ∑ i = 1 n 1 2 log ( 2 π σ 2 ) + 1 2 σ 2 ( y ( i ) − w ⊤ x ( i ) − b ) 2 -\log P(\mathbf{y}\mid\mathbf{X})=\sum_{i=1}^n\frac12\log(2\pi\sigma^2)+\frac1{2\sigma^2}\left(y^{(i)}-\mathbf{w}^\top\mathbf{x}^{(i)}-b\right)^2 −logP(y∣X)=i=1∑n21log(2πσ2)+2σ21(y(i)−w⊤x(i)−b)2
import math
import numpy as np
import matplotlib.pyplot as plt
def normal(x, mu, sigma):
p = 1 / math.sqrt(2 * math.pi * sigma**2)
return p * np.exp(-0.5 / sigma ** 2 * (x - mu) ** 2)
x = np.arange(-7, 7, 0.01)
# 改变均值会产生沿 x 轴的偏移,增加方差将会分散分布、降低峰值
params = [(0, 1), (0, 2), (3, 1)]
plt.figure(figsize=(8, 6))
for mu, sigma in params:
plt.plot(x, normal(x, mu, sigma), label=f'mean {mu}, std {sigma}')
plt.xlabel('x')
plt.ylabel('p(x)')
plt.legend()
plt.show()
1.1.4 从线性回归到深度网络
神经网络图
-
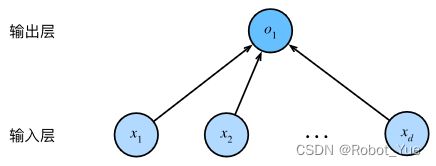
下图所示的神经网络中
- 输入为 x 1 , … , x d x_{1},\ldots,x_{d} x1,…,xd,因此输入层中的输入数 (或称为特征维度)为 d d d
- 网络的输出为 o 1 o_1 o1,因此输出层中的输出数是 1
-
输入值都是已经给定的,并且只有一个计算神经元。由于模型重点在发生计算的地方,所以通常在计算层数时不考虑输入层。也就是说,下图中神经网络的层数为 1
-
可以将线性回归模型视为仅由单个人工神经元组成的神经网络,或称为单层神经网络。对于线性回归,每个输入都与每个输出(在本例中只有一个输出)相连,将这种变换 (图中的输出层) 称为全连接层 (fully-connected laver) 或称为稠密层 (dense laver)
1.2 线性回归的简洁实现
1.2.1 生成数据集
- 生成一个包含 1000 个样本的数据集,每个样本包含从标准正态分布中采样的 2 个特征。合成数据集是一个矩阵 x ∈ R 1000 × 2 \mathbf{x}\in\mathbb{R}^{1000\times2} x∈R1000×2
- 使用线性模型参数 w = [ 2 , − 3.4 ] T , b = 4.2 \mathbf{w}=[2,-3.4]^{\mathsf{T}},b=4.2 w=[2,−3.4]T,b=4.2 和噪声项 ϵ \epsilon ϵ 生成数据集及其标签
- ϵ \epsilon ϵ 可视为模型预测和标签时的潜在观测误差,假设 ϵ \epsilon ϵ 服从均值为 0 的正态分布,此处将标准差设为 0.01
y = X w + b + ϵ \mathbf{y}=\mathbf{X}\mathbf{w}+b+\epsilon y=Xw+b+ϵ
import numpy as np import torch from torch.utils import data def synthetic_data(w, b, num_examples): X = torch.normal(0, 1, (num_examples, len(w))) y = torch.matmul(X, w) + b y += torch.normal(0, 0.01, y.shape) return X, y.reshape((-1, 1)) true_w = torch.tensor([2, -3.4]) true_b = 4.2 features, labels = synthetic_data(true_w, true_b, 1000) - ϵ \epsilon ϵ 可视为模型预测和标签时的潜在观测误差,假设 ϵ \epsilon ϵ 服从均值为 0 的正态分布,此处将标准差设为 0.01
1.2.2 读取数据集
- 调用框架中现有的 API 来读取数据。将 features 和 labels 作为 API 的参数传递,并通过数据迭代器指定 batch_size。此外,布尔值 is_train 表示是否希望数据迭代器对象在每个迭代周期内打乱数据
def load_array(data_arrays, batch_size, is_train=True): dataset = data.TensorDataset(*data_arrays) return data.DataLoader(dataset, batch_size, shuffle=is_train) batch_size = 10 data_iter = load_array((features, labels), batch_size) # 为了验证是否正常工作,读取并打印第一个小批量样本 # 使用 iter 构造 Python 迭代器,并使用 next 从迭代器中获取第一项 print(next(iter(data_iter)))# 输出 [tensor([[ 1.0829, -0.0883], [ 0.0989, 0.7460], [ 1.0245, -0.1956], [-0.7932, 1.7843], [ 1.2336, 1.0276], [ 2.1166, 0.2072], [-0.1430, 0.4944], [ 0.7086, 0.3950], [-0.0851, 1.4635], [ 0.2977, 1.8625]]), tensor([[ 6.6616], [ 1.8494], [ 6.9229], [-3.4516], [ 3.1747], [ 7.7283], [ 2.2302], [ 4.2612], [-0.9383], [-1.5352]])]
1.2.3 定义模型
- 对于标准深度学习模型,可使用框架的预定义好的层,只需关注使用哪些层来构造模型,而不必关注层的实现细节
- 在 PyTorch 中,全连接层在 Linear 类中定义。值得注意的是,将两个参数传递到 nn.Linear 中
- 第一个指定输入特征形状,即 2
- 第二个指定输出特征形状(单个标量),为 1
from torch import nn net = nn.Sequential(nn.Linear(2, 1))
1.2.4 初始化模型参数
- 使用 net 之前需要初始化模型参数,如:在线性回归模型中的权重和偏置。深度学习框架通常有预定义的方法来初始化参数。在这里,指定每个权重参数应该从均值为 0、标准差为 0.01 的正态分布中随机采样,偏置参数将初始化为零
net[0].weight.data.normal_(0, 0.01) net[0].bias.data.fill_(0)
1.2.5 定义损失函数
- 计算均方误差使用的是 MSELoss 类,也称为平方 L 2 L_2 L2 范数。默认情况下,它返回所有样本损失的平均值
loss = nn.MSELoss()
1.2.6 定义优化算法
- 小批量随机梯度下降算法是一种优化神经网络的标准工具,PyTorch 在 optim 模块中实现了该算法的许多变种。当实例化一个 SGD 实例时,要指定优化的参数以及优化算法所需的超参数字典。小批量随机梯度下降只需要设置 lr 值,这里设置为 0.03
trainer = torch.optim.SGD(net.parameters(), lr=0.03)
1.2.7 训练
- 在每个迭代周期,将完整遍历一次数据集,不停从中获取一个小批量的输入和相应的标签。对每一个小批量,进行以下步骤
- 通过调用 net(X) 生成预测并计算损失 l (前向传播)
- 通过进行反向传播来计算梯度
- 通过调用优化器来更新模型参数
- 为了更好的衡量训练效果,计算每个迭代周期后的损失,并打印它来监控训练过程
num_epochs = 3 for epoch in range(num_epochs): for X, y in data_iter: l = loss(net(X) ,y) trainer.zero_grad() l.backward() trainer.step() l = loss(net(features), labels) print(f'epoch {epoch + 1}, loss {l:f}') - 代码汇总
import numpy as np import torch from torch.utils import data from torch import nn # 生成数据集 def synthetic_data(w, b, num_examples): X = torch.normal(0, 1, (num_examples, len(w))) y = torch.matmul(X, w) + b y += torch.normal(0, 0.01, y.shape) return X, y.reshape((-1, 1)) true_w = torch.tensor([2, -3.4]) true_b = 4.2 features, labels = synthetic_data(true_w, true_b, 1000) # 读取数据集 def load_array(data_arrays, batch_size, is_train=True): dataset = data.TensorDataset(*data_arrays) return data.DataLoader(dataset, batch_size, shuffle=is_train) batch_size = 10 data_iter = load_array((features, labels), batch_size) # 定义模型 net = nn.Sequential(nn.Linear(2, 1)) # 初始化模型参数 net[0].weight.data.normal_(0, 0.01) net[0].bias.data.fill_(0) # 定义损失函数 loss = nn.MSELoss() # 定义优化算法 trainer = torch.optim.SGD(net.parameters(), lr=0.03) # 训练 num_epochs = 3 for epoch in range(num_epochs): for X, y in data_iter: l = loss(net(X) ,y) trainer.zero_grad() l.backward() trainer.step() l = loss(net(features), labels) print(f'epoch {epoch + 1}, loss {l:f}') w = net[0].weight.data print('w的估计误差:', true_w - w.reshape(true_w.shape)) b = net[0].bias.data print('b的估计误差:', true_b - b)# 输出 epoch 1, loss 0.000216 epoch 2, loss 0.000104 epoch 3, loss 0.000102 w的估计误差: tensor([-0.0002, 0.0004]) b的估计误差: tensor([0.0002])
1.3 softmax 回归
1.3.1 分类问题
- 从一个图像分类问题开始。假设每次输入是一个 2 x 2 的灰度图像。可以用一个标量表示每个像素值,每个图像对应四个特征 x 1 , x 2 , x 3 , x 4 x_{1},x_{2},x_{3},x_{4} x1,x2,x3,x4。此外,假设每个图像属于类别 “猫” “鸡” 和 “狗” 中的一个
- 一种表示分类数据的简单方法:独热编码 (one-hot encoding)。独热编码是一个向量,它的分量和类别一样多。类别对应的分量设置为 1,其他所有分量设置为 0。在本例中,标签 y y y 将是一个三维向量,其中 (1,0,0) 对应于 “猫”、(0,1,0) 对应于 “鸡”、(0,0,1) 对应于 “狗”
y ∈ { ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) , ( 0 , 0 , 1 ) } y\in\{(1,0,0),(0,1,0),(0,0,1)\} y∈{(1,0,0),(0,1,0),(0,0,1)}
1.3.2 网络架构
-
为估计所有可能类别的条件概率,需要一个有多个输出的模型,每个类别对应一个输出。为了解决线性模型的分类问题,需要和输出一样多的仿射函数。每个输出对应于它自己的仿射函数。本例中有 4 个特征和 3 个可能的输出类别,因此将需要 12 个标量来表示权重 (带下标的 w w w),3 个标量来表示偏置 (带下标的 b b b)。下面为每个输入计算三个未规范化的预测 (logit): o 1 , o 2 和 o 3 o_1,o_2\text{和}o_3 o1,o2和o3
o 1 = x 1 w 11 + x 2 w 12 + x 3 w 13 + x 4 w 14 + b 1 , o 2 = x 1 w 21 + x 2 w 22 + x 3 w 23 + x 4 w 24 + b 2 , o 3 = x 1 w 31 + x 2 w 32 + x 3 w 33 + x 4 w 34 + b 3 . \begin{aligned}o_1&=x_1w_{11}+x_2w_{12}+x_3w_{13}+x_4w_{14}+b_1,\\o_2&=x_1w_{21}+x_2w_{22}+x_3w_{23}+x_4w_{24}+b_2,\\o_3&=x_1w_{31}+x_2w_{32}+x_3w_{33}+x_4w_{34}+b_3.\end{aligned} o1o2o3=x1w11+x2w12+x3w13+x4w14+b1,=x1w21+x2w22+x3w23+x4w24+b2,=x1w31+x2w32+x3w33+x4w34+b3. -
可以用神经网络图描述这个计算过程。与线性回归一样,softmax 回归也是一个单层神经网络由于计算每个输出 o 1 , o 2 和 o 3 o_1,o_2\text{和}o_3 o1,o2和o3 取决于所有输入 x 1 , x 2 , x 3 和 x 4 x_{1},x_{2},x_{3}\text{和}x_{4} x1,x2,x3和x4,所以 softmax 回归的输出层也是全连接层
1.3.3 全连接层的参数开销
- 全连接层是 “完全” 连接的,可能有很多可学习的参数。具体来说,对于任何具有 d d d 个输入和 q q q 个输出的全连接层,参数开销为 O ( d q ) \mathcal{O}(dq) O(dq)。将 d d d 个输入转换为 q q q 个输出的成本可以减少到 O ( d q n ) \mathcal{O}({\frac{dq}{n}}) O(ndq),其中超参数 n n n 可以灵活指定,以在实际应用中平衡参数节约和模型有效性
1.3.4 softmax 运算
-
softmax 函数能够将未规范化的预测变换为非负数并且总和为 1,同时让模型保持可导的性质。为了完成这一目标,首先对每个未规范化的预测求幂,这样可以确保输出非负。为了确保最终输出的概率值总和为 1,再让每个求幂后的结果除以它们的总和
y ^ = s o f t m a x ( o ) 其中 y ^ j = exp ( o j ) ∑ k exp ( o k ) \hat{\mathbf{y}}=\mathrm{softmax}(\mathbf{o})\quad\text{其中}\quad\hat{y}_j=\frac{\exp(o_j)}{\sum_k\exp(o_k)} y^=softmax(o)其中y^j=∑kexp(ok)exp(oj) -
尽管softmax是一个非线性函数,但 softmax 回归的输出仍然由输入特征的仿射变换决定。因此 softmax 回归是一个线性模型
1.3.5 小批量样本的矢量化
- 为了提高计算效率并且充分利用 GPU,通常会对小批量样本的数据执行矢量计算。softmax 回归的矢量计算表达式为
O = X W + b , Y ^ = s o f t m a x ( O ) \begin{aligned}\mathbf{O}&=\mathbf{X}\mathbf{W}+\mathbf{b},\\\hat{\mathbf{Y}}&=\mathrm{softmax}(\mathbf{O})\end{aligned} OY^=XW+b,=softmax(O)
1.3.6 损失函数
- 略,基本同线性回归
1.3.7 信息论基础
-
信息论 (information theory) 涉及编码、解码、发送以及尽可能简洁地处理信息或数据
-
信息论的核心思想是量化数据中的信息内容,该数值被称为分布 P P P 的熵 (entropy)
H [ P ] = ∑ j − P ( j ) log P ( j ) H[P]=\sum_j-P(j)\log P(j) H[P]=j∑−P(j)logP(j)
1.3.8 模型预测和评估
- 在训练 softmax 回归模型后,给出任何样本特征,可以预测每个输出类别的概率。通常使用预测概率最高的类别作为输出类别。如果预测与实际类别 (标签) 一致,则预测是正确的。使用精度来评估模型的性能,精度等于正确预测数与预测总数之间的比率
1.4 图像分类数据集
1.4.1 读取数据集
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
import matplotlib.pyplot as plt
# 通过 ToTensor 实例将图像数据从 PIL 类型变换成 32 位浮点数格式
# 并除以 255 使得所有像素的数值均在 0~1 之间
trans = transforms.ToTensor()
# root:指定数据集下载或保存的路径;train:指定加载的是训练数据集还是测试数据集
# transform:指定数据集的转换操作;download:指定是否下载数据集
mnist_train = torchvision.datasets.FashionMNIST(
root="./data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
root="./data", train=False, transform=trans, download=True)
# 将标签转换成对应的类别名称
def get_fashion_mnist_labels(labels):
text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
# 这是一个列表推导式
# 1.将 labels 中的每个元素按照索引转换为对应的文本标签
# 2.然后将这些元素组成一个新的列表并返回
return [text_labels[int(i)] for i in labels]
def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):
figsize = (num_cols * scale, num_rows * scale)
# 第一个变量_是一个通用变量名,通常用于表示一个不需要使用的值
# 第二个变量 axes 是一个包含所有子图对象的数组
# 这里使用这种命名约定是为了表示只关心 axes 而不关心第一个返回值
_, axes = plt.subplots(num_rows, num_cols, figsize=figsize)
axes = axes.flatten() # 将 axes 展平为一维数组
# 遍历 axes 和 imgs 的元素,其中 i 为索引,ax 为当前子图,img 为当前图像
for i, (ax, img) in enumerate(zip(axes, imgs)):
if isinstance(img, torch.Tensor): # img 是一个 torch.Tensor 类型
# img 是一个张量,假设其形状为 (C, H, W),其中 C 代表通道数,H 代表高度,W 代表宽度
# permute(1, 2, 0) 是对 img 进行维度重排操作。它将维度从 (C, H, W) 重排为 (H, W, C)
ax.imshow(img.permute(1, 2, 0))
else:
ax.imshow(img)
ax.axis('off') # 关闭图像的坐标轴
if titles:
ax.set_title(titles[i])
plt.show()
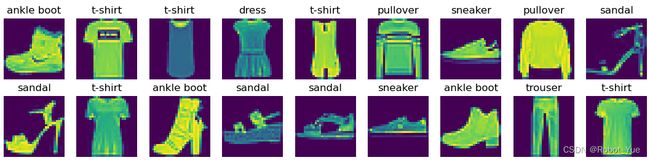
X, y = next(iter(data.DataLoader(mnist_train, batch_size=18)))
show_images(X, 2, 9, titles=get_fashion_mnist_labels(y))
1.4.2 读取小批量
- 为了在读取训练集和测试集时更容易,使用内置的数据迭代器,而不是从零开始创建。在每次迭代中,数据加载器每次都会读取一小批量数据,大小为 batch_size。通过内置数据迭代器,可以随机打乱所有样本,从而无偏见地读取小批量
- 当处理较大的数据集时,一次向网络喂入全部数据得不到很好的训练效果。通常将整个样本的数量分成多个批次 batch,每个 batch 中样本的个数叫做样本大小 batch_size
batch_size = 256 def get_dataloader_workers(): return 4 # 使用 4 个进程来读取数据 train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers())
1.4.3 整合所有组件
- 现在定义 load_data_fashion_mnist 函数,用于获取和读取 Fashion-MNIST 数据集。这个函数返回训练集和验证集的数据迭代器。此外,这个函数还接受一个可选参数 resize,用来将图像大小调整为另一种形状
def load_data_fashion_mnist(batch_size, resize=None): # 下载 Fashion-MNIST 数据集,然后将其加载到内存中 trans = [transforms.ToTensor()] if resize: trans.insert(0, transforms.Resize(resize)) trans = transforms.Compose(trans) mnist_train = torchvision.datasets.FashionMNIST( root="./data", train=True, transform=trans, download=True) mnist_test = torchvision.datasets.FashionMNIST( root="./data", train=False, transform=trans, download=True) return (data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers()), data.DataLoader(mnist_test, batch_size, shuffle=False, num_workers=get_dataloader_workers()))
1.5 softmax 回归的简洁实现
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
# 设置随机种子以确保结果可重复
torch.manual_seed(42)
# 定义超参数
batch_size = 128 # 每个批次的样本数
learning_rate = 0.1 # 学习率,用于控制优化过程中参数更新的步长
num_epochs = 100 # 训练的轮数
# 加载 Fashion-MNIST 数据集
transform = transforms.Compose([
transforms.ToTensor(), # 将图像转换为张量
transforms.Normalize((0.5,), (0.5,)) # 将像素值归一化到 [-1,1] 区间
])
# 加载训练集和测试集,并将数据转换为张量
train_dataset = torchvision.datasets.FashionMNIST(root='./data', train=True, download=True, transform=transform)
test_dataset = torchvision.datasets.FashionMNIST(root='./data', train=False, download=True, transform=transform)
# 创建训练集和测试集的数据加载器,用于批量获取数据
train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False)
# 定义模型
# 创建了一个名为 SoftmaxRegression 的类,继承自 nn.Module
class SoftmaxRegression(nn.Module):
def __init__(self, input_size, num_classes): # 构造函数 init 初始化
super(SoftmaxRegression, self).__init__()
# 定义了一个线性层 (nn.Linear) 作为模型的唯一层次结构
# 输入大小为 input_size,输出大小为 num_classes
self.linear = nn.Linear(input_size, num_classes)
# 实现了前向传播操作,将输入数据通过线性层得到输出
def forward(self, x):
out = self.linear(x)
return out
model = SoftmaxRegression(input_size=784, num_classes=10)
# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss() # 用于计算多分类问题中的交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=learning_rate) # 定义随机梯度下降优化器,用于更新模型的参数
# 训练模型
train_losses = []
test_losses = []
# 在模型训练的过程中,运行模型对全部数据完成一次前向传播和反向传播的完整过程叫做一个 epoch
# 在梯度下降的模型训练的过程中,神经网络逐渐从不拟合状态到优化拟合状态,达到最优状态之后会进入过拟合状态
# 因此 epoch 并非越大越好。数据越多样,相应 epoch 就越大
for epoch in range(num_epochs):
train_loss = 0.0
# 1.将模型设置为训练模式
model.train()
for images, labels in train_loader:
# 将输入数据展平
images = images.reshape(-1, 784)
# 前向传播、计算损失、反向传播和优化
outputs = model(images)
loss = criterion(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_loss += loss.item()
# 2.将模型设置为评估模式(在测试集上计算损失)
model.eval()
test_loss = 0.0
correct = 0
total = 0
with torch.no_grad():
for images, labels in test_loader:
images = images.reshape(-1, 784)
outputs = model(images)
loss = criterion(outputs, labels)
test_loss += loss.item()
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
train_loss /= len(train_loader)
test_loss /= len(test_loader)
accuracy = 100 * correct / total
train_losses.append(train_loss)
test_losses.append(test_loss)
print(f'Epoch [{epoch + 1}/{num_epochs}], Train Loss: {train_loss:.4f}, Test Loss: {test_loss:.4f}, Accuracy: {accuracy:.2f}%')
# 可视化损失
plt.plot(train_losses, label='Train Loss')
plt.plot(test_losses, label='Test Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.show()
# 输出
Epoch [1/100], Train Loss: 0.6287, Test Loss: 0.5182, Accuracy: 81.96%
Epoch [2/100], Train Loss: 0.4887, Test Loss: 0.4981, Accuracy: 82.25%
Epoch [3/100], Train Loss: 0.4701, Test Loss: 0.4818, Accuracy: 82.49%
Epoch [4/100], Train Loss: 0.4554, Test Loss: 0.4719, Accuracy: 82.90%
Epoch [5/100], Train Loss: 0.4481, Test Loss: 0.4925, Accuracy: 82.57%
Epoch [6/100], Train Loss: 0.4360, Test Loss: 0.4621, Accuracy: 83.53%
Epoch [7/100], Train Loss: 0.4316, Test Loss: 0.4662, Accuracy: 83.53%
Epoch [8/100], Train Loss: 0.4293, Test Loss: 0.4543, Accuracy: 83.80%
Epoch [9/100], Train Loss: 0.4289, Test Loss: 0.5460, Accuracy: 81.09%
...