PageRank&ConnectedComponents&Pregel
PageRank&ConnectedComponents&Pregel
一 PageRank算法

实例实现
下面为社交网络关系图,求出最受欢迎的一个人,即直接或间接入度最多的。
import org.apache.spark.rdd.RDD
import org.apache.spark.{SparkConf, SparkContext}
import org.apache.spark.graphx._
object pageRank {
def main(args: Array[String]): Unit = {
val conf: SparkConf = new SparkConf().setMaster("local[*]").setAppName("pagerank")
val sc = new SparkContext(conf)
/*
type VertexId = scala.Long
type PartitionID = scala.Int
*/
val info: RDD[(VertexId, (String, PartitionID))] = sc.makeRDD(Array((1L,("Alice",28)),(2L,("Bob",27)),(3L,("Charlie",65)),(4L,("David",42)),(5L,("Ed",55)),(6L,("Fran",50))))
val rela=sc.makeRDD(Array(Edge(2L,1L,7),Edge(3L,2L,4),Edge(4L,1L,1),Edge(2L,4L,2),Edge(5L,2L,2),Edge(5L,3L,8),Edge(5L,6L,3),Edge(3L,6L,3)))
val graph: Graph[(String, PartitionID), PartitionID] = Graph(info,rela)
val pageGraph: Graph[Double, Double] = graph.pageRank(0.001,0.15)
//精度为0.001,重置概率为0.15,因为5号用户没有任何入度,所以其跳转概率即为0.15
pageGraph.vertices.sortBy(-_._2).collect().foreach(println)
}
}
/*
(1,0.49317820312499994)
(2,0.27431249999999996)
(6,0.27431249999999996)
(4,0.2665828125)
(3,0.1925)
(5,0.15)
PageRank算法原理剖析
如有需要,请点击下方链接获取
链接: PageRank算法原理剖析及Spark实现_白 杨的博客-CSDN博客
二 ConnectedComponents
数据准备
people.csv
4,Dave,25
6,Faith,21
8,Harvey,47
2,Bob,18
1,Alice,20
3,Charlie,30
7,George,34
9,Ivy,21
5,Eve,30
10,Lily,35
11,Helen,35
12,Ann,35
links.csv
1,2,friend
1,3,sister
2,4,brother
3,2,boss
4,5,client
1,9,friend
6,7,cousin
7,9,coworker
8,9,father
10,11,colleague
10,12,colleague
11,12,colleague
图结构

实现
经过connectedComponents得到的结果,可以知道哪些顶点在一个连通图中,这样就可以将一个大图拆分成若干个连通子图。
代码
import org.apache.spark.rdd.RDD
import org.apache.spark.{SparkConf, SparkContext}
import org.apache.spark.graphx._
object ConnectedComponentsDemo {
def main(args: Array[String]): Unit = {
val conf: SparkConf = new SparkConf().setMaster("local[*]").setAppName("connectedComponents")
val sc = new SparkContext(conf)
case class Person(name:String,age:Int)
val peopleRDD: RDD[(VertexId, Person)] = sc.textFile("in/suanfa/people.csv")
.map(_.split(","))
.map(x => (x(0).toLong, Person(x(1), x(2).toInt)))
val linksRDD: RDD[Edge[String]] = sc.textFile("in/suanfa/links.csv").map(x => {
val row = x.split(",")
Edge(row(0).toLong, row(1).toLong, row(2))
})
val graph: Graph[Person, String] = Graph(peopleRDD,linksRDD)
val conn: Graph[VertexId, String] = graph.connectedComponents()
conn.vertices.collect().foreach(println)
结果
(4,1)
(6,1)
(8,1)
(12,10)
(10,10)
(2,1)
(11,10)
(1,1)
(3,1)
(7,1)
(9,1)
(5,1)
从结果中可以看到通过计算之后的图,每个顶点原先的属性变成了这个顶点所在的连通图中的最小顶点id。
扩展
通过connectedComponents得到的新图的顶点属性已经没有了原始的那些信息,所以需要和原始信息RDD作一个outerJoinVertices去得到原始的信息
通过连通图中最小顶点编号,使用subgraph方法得到每个连通子图
//此时conn的顶点属性变成了联通图中最小的顶点号,所以我们外联一个peopleRDD得到以往的属性
val newGraph: Graph[(VertexId, String, PartitionID), String] = conn
.outerJoinVertices(peopleRDD)((id,minid,p)=>(minid,p.get.name,p.get.age))
//newGraph.vertices.collect().foreach(println)
conn.vertices.map(_._2).collect().distinct.foreach(id=>{//得到所有连通图中id最小的顶点编号并去重
//通过连通图中最小顶点编号,使用subgraph方法得到每个连通子图
val sub: Graph[(VertexId, String, PartitionID), String] = newGraph.subgraph(vpred = (VertexID,prop)=>prop._1==id)
//打印联通子图
// sub.triplets.collect().foreach(println)
// println()
//上下等价
println(sub.triplets.collect().mkString(",")) //用数组方法打印
})
}
}
/*
((1,(1,Alice,20)),(2,(1,Bob,18)),friend),((1,(1,Alice,20)),(3,(1,Charlie,30)),sister),((1,(1,Alice,20)),(9,(1,Ivy,21)),friend),((2,(1,Bob,18)),(4,(1,Dave,25)),brother),((3,(1,Charlie,30)),(2,(1,Bob,18)),boss),((4,(1,Dave,25)),(5,(1,Eve,30)),client),((6,(1,Faith,21)),(7,(1,George,34)),cousin),((7,(1,George,34)),(9,(1,Ivy,21)),coworker),((8,(1,Harvey,47)),(9,(1,Ivy,21)),father)
((10,(10,Lily,35)),(11,(10,Helen,35)),colleague),((10,(10,Lily,35)),(12,(10,Ann,35)),colleague),((11,(10,Helen,35)),(12,(10,Ann,35)),colleague)
参考
链接:csdn - 安全中心GraphX之Connected Components - 简书csdn - 安全中心
三 Pregel
pregel函数源码
def pregel[A: ClassTag](
initialMsg: A,
maxIterations: Int = Int.MaxValue,
activeDirection: EdgeDirection = EdgeDirection.Either)(
vprog: (VertexId, VD, A) => VD,
sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
mergeMsg: (A, A) => A)
: Graph[VD, ED] = {
Pregel(graph, initialMsg, maxIterations, activeDirection)(vprog, sendMsg, mergeMsg)
}
initialMsg:图初始化的时候,开始模型计算的时候,所有节点都会先收到一个消息
maxIterations:将要执行的最大迭代次数
activeDirection:发送消息方向(默认是出边方向:EdgeDirection.Out)
vprog:用户定义函数,用于顶点接收消息
sendMsg:用户定义的函数,用于确定下一个迭代发送的消息及发往何处
mergeMsg:用户定义的函数,如果一个节点接收到多条消息,先用mergeMsg 来将多条消息聚合成为一条消息,如果节点只收到一条消息,则不调用该函数
顶点的激活态和钝化态
顶点 的状态有两种:
钝化态【类似于休眠,不做任何事】
激活态【干活】
顶点 能够处于激活态需要有条件:
成功收到消息
成功发送了任何一条消息
pregel原理分析
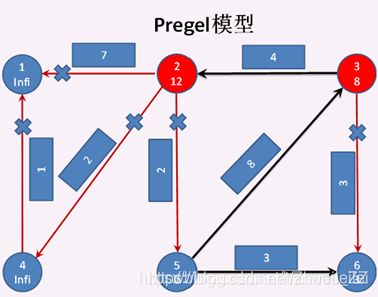
调用pregel方法之前,先把图的各个顶点的属性初始化为如下图所示:顶点5到自己的距离为0,所以设为0,其他顶点都设为 正无穷大Double.PositiveInfinity
当调用pregel方法开始:
首先,所有顶点都将接收到一条初始消息initialMsg ,使所有顶点都处于激活态(红色标识的节点)。
第一次迭代开始:
所有顶点以EdgeDirection.Out的边方向调用sendMsg方法发送消息给目标顶点,如果 源顶点的属性+边的属性<目标顶点的属性,则发送消息成功。否则不发送。
发送成功的只有两条边:
5—>3(0+8
3—>6(Double.Infinity+3>Double.Infinity , 失败)
2—>1(Double.Infinity+7>Double.Infinity , 失败)
2—>4(Double.Infinity+2>Double.Infinity , 失败)
2—>5(Double.Infinity+2>Double.Infinity , 失败)
4—>1(Double.Infinity+1>Double.Infinity , 失败)。
sendMsg方法执行完成之后,根据顶点处于激活态的条件,顶点5 成功地分别给顶点3 和 顶点6 发送了消息,顶点3 和 顶点6 也成功地接受到了消息。所以 此时只有5,3,6 三个顶点处于激活态,其他顶点全部钝化。然后收到消息的顶点3和顶点6都调用vprog方法,将收到的消息 与 自身的属性合并。如下图所示。到此第一次迭代结束。

第二次迭代开始:
顶点3 给 顶点6 发送消息失败,顶点3 给 顶点2 发送消息成功,此时 顶点3 成功发送消息,顶点2 成功接收消息,所以顶点2 和 顶点3 都成为激活状态,其他顶点都成为钝化状态。然后顶点2 调用vprog方法,将收到的消息 与 自身的属性合并。见下图。 至此第二次迭代结束。
第三次迭代开始:
顶点3分别发送消息给顶点2失败 和 顶点6失败,顶点2 分别发消息给 顶点1成功、顶点4成功、顶点5失败 ,所以 顶点2、顶点1、顶点4 成为激活状态,其他顶点为钝化状态。顶点1 和 顶点4分别调用vprog方法,将收到的消息 与 自身的属性合并。见下图。至此第三次迭代结束
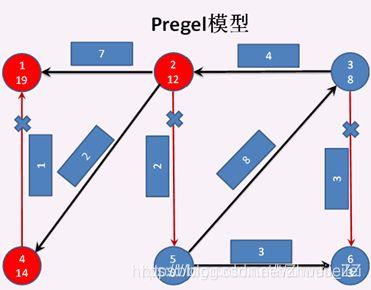
第四次迭代开始:
顶点2 分别发送消息给 顶点1失败 和 顶点4失败。顶点4 给 顶点1发送消息成功,顶点1 和 顶点4 进入激活状态,其他顶点进入钝化状态。顶点1 调用vprog方法,将收到的消息 与 自身的属性合并 。见下图
第五次迭代开始:
顶点4 再给 顶点1发送消息失败,顶点4 和 顶点1 进入钝化状态,此时全图都进入钝化状态。至此结束,见下图
pregel代码实现
ache.spark.graphx.VertexId
import org.ap
package suanfa
import org.ap
ache.spark.rdd.RDD
import org.apache.spark.{SparkConf, SparkContext, graphx}
import org.apache.spark.graphx._
object pregelDemo {
def main(args: Array[String]): Unit = {
//1、创建SparkContext
val sparkConf = new SparkConf().setAppName("GraphxHelloWorld").setMaster("local[*]")
val sc = new SparkContext(sparkConf)
//2、创建顶点
val vertexArray = Array(
(1L, ("Alice", 28)),
(2L, ("Bob", 27)),
(3L, ("Charlie", 65)),
(4L, ("David", 42)),
(5L, ("Ed", 55)),
(6L, ("Fran", 50))
)
val vertexRDD: RDD[(VertexId, (String,Int))] = sc.makeRDD(vertexArray)
//3、创建边,边的属性代表 相邻两个顶点之间的距离
val edgeArray = Array(
Edge(2L, 1L, 7),
Edge(2L, 4L, 2),
Edge(3L, 2L, 4),
Edge(3L, 6L, 3),
Edge(4L, 1L, 1),
Edge(2L, 5L, 2),
Edge(5L, 3L, 8),
Edge(5L, 6L, 3)
)
val edgeRDD: RDD[Edge[Int]] = sc.makeRDD(edgeArray)
//4、创建图(使用apply方法创建)
val graph: Graph[(String, PartitionID), PartitionID] = Graph(vertexRDD, edgeRDD)
/* ************************** 使用pregle算法计算 ,顶点5 到 各个顶点的最短距离 ************************** */
//5、定义图中起始顶点id
val srcVertexId=5L
//6、修改顶点属性,起始顶点为0,其余全部为正无穷大
val initialGraph=graph.mapVertices((id,prop)=>{
if(id==srcVertexId)
0
else
Double.PositiveInfinity
})
//7、调用pregel
val pregelGraph: Graph[Double, PartitionID] = initialGraph.pregel(
Double.PositiveInfinity,
Int.MaxValue,
EdgeDirection.Out
)(
//接收消息函数:接收下面sendMsg的信息
(vid: VertexId, vd: Double, distMsg: Double) => {
//返回相同VertexId的情况下,发送顶点的属性加上边属性和与目标顶点属性的最小值
val minDist: Double = math.min(vd, distMsg)
println(s"顶点${vid},属性${vd},收到消息${distMsg},合并后的属性${minDist}")
minDist
},
//发送消息函数:先发送后接受,所以先执行这一步
(edgeTriplet: EdgeTriplet[Double, PartitionID]) => {
if (edgeTriplet.srcAttr + edgeTriplet.attr < edgeTriplet.dstAttr) { //如果发送顶点的属性加上边属性小于目标顶点属性
println(s"顶点${edgeTriplet.srcId} 给 顶点${edgeTriplet.dstId} 发送消息 ${edgeTriplet.srcAttr + edgeTriplet.attr}")
//则返回一个(目标顶点id,发送顶点属性加上边属性)
Iterator[(VertexId, Double)]((edgeTriplet.dstId, edgeTriplet.srcAttr + edgeTriplet.attr))
} else { //否则返回空,即消息发送失败
Iterator.empty
}
},
//合并消息函数:指有两个及以上的激活态顶点给同一个顶点发送消息,且都发送成功,则执行完sendMsg后调用mergeMsg再执行vprog
(msg1: Double, msg2: Double) =>{
println("mergeMsg:",msg1,msg2) //本次demo没有符合条件的,所以没有调用
math.min(msg1, msg2) //返回各自激活态顶点属性加上各自边的属性之和的最小值进入vprog函数
}
)
pregelGraph
//8、输出结果
println("******打印pregel的新图的vertices信息******")
//vertices属性代表着5号顶点到各顶点的最短距离
pregelGraph.vertices.collect().foreach(println)
//上下等价
// println(pregelGraph.vertices.collect().mkString("\n"))
}
}
/*
顶点3,属性Infinity,收到消息Infinity,合并后的属性Infinity
顶点2,属性Infinity,收到消息Infinity,合并后的属性Infinity
顶点4,属性Infinity,收到消息Infinity,合并后的属性Infinity
顶点1,属性Infinity,收到消息Infinity,合并后的属性Infinity
顶点5,属性0.0,收到消息Infinity,合并后的属性0.0
顶点6,属性Infinity,收到消息Infinity,合并后的属性Infinity
顶点5 给 顶点3 发送消息 8.0
顶点5 给 顶点6 发送消息 3.0
顶点3,属性Infinity,收到消息8.0,合并后的属性8.0
顶点6,属性Infinity,收到消息3.0,合并后的属性3.0
顶点3 给 顶点2 发送消息 12.0
顶点2,属性Infinity,收到消息12.0,合并后的属性12.0
顶点2 给 顶点1 发送消息 19.0
顶点2 给 顶点4 发送消息 14.0
顶点1,属性Infinity,收到消息19.0,合并后的属性19.0
顶点4,属性Infinity,收到消息14.0,合并后的属性14.0
顶点4 给 顶点1 发送消息 15.0
顶点1,属性19.0,收到消息15.0,合并后的属性15.0
******打印pregel的新图的vertices信息******
(1,15.0)
(2,12.0)
(3,8.0)
(4,14.0)
(5,0.0)
(6,3.0)
代码分析
需要注意的一点就是虽然pregel后三个自定义函数本身位置顺序不能变,但其实它们执行的顺序并不是从上而下的
结合代码来看,先执行sendMsg判断各个顶点发送消息能否成功,执行结果返回一个发送顶点及边属性之和
如果同时有多个激活态的顶点向一个顶点发送消息且发送成功的话,他们各自返回结果会进入mergeMsg比较返回一个最小值进入第三步vprog,否则就不会执行mergeMsg直接进入vprog
上一步的返回结果,发送顶点及边属性之和进入vprog后会与目标顶点的本身属性比较,返回一个最小值成为目标顶点的新的属性。
参考:
链接: Spark GraphX 中的 pregel函数_Bamdli的博客-CSDN博客
转自:<Zhuuu_ZZ>Spark GraphX中的三大算法PageRank&ConnectedComponents&Pregel_Zhuuu_ZZ的博客-CSDN博客