代码随想录算法训练营第七天|454题.四数相加II 383. 赎金信 15. 三数之和 18. 四数之和
454题.四数相加
-
- 根据题目需求移动指针，有移动小的那方的
题目链接
有点类似于两数之和,还是用map,就是先把两数之和放到map里,然后再从这个里面找与c+d之和为0的值即0-(c+d)
有点割裂的意思,把这个分成了两部分,但题目统计的是出现的次数,那么可能和也有出现相同的但是是不同的值组成的.
所以和的出现次数也是一个要记录的值,所以就用,map,但是要保留原有的位置不用排序,那就应该选择unordered_map来作为存储{和,次数}这里就用到了如何给map的值(value)赋值的问题,就像数组一样,只不过这里的下标为键,而元素的值为值,在这里只和出现的次数
就是在利用map求某几个数之和=一个确定的数的时候,要学会分组,然后通过反向求解如做差来表示已知map里的值,看map里面有没有
.
class Solution {
public:
int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
unordered_map<int,int >umap;
for(int a:nums1)
for(int b:nums2){//如何给map这个容器赋值:,中括号里是键,=后是值(这里表示这个值出现的次数)(或者可以理解为整体是个值,长得像个数组元素)
umap[a+b]++;
}
int count= 0;
for(int c:nums3){
for(int d:nums4){
if( umap.find(0-(c+d))!=umap.end()){
count+=umap[0-(c+d)];
}
}
}return count;
}
};
总体思路就是先往map里赋值,然后再求另一部分的和的时候在map里找值
383. 赎金信
-
- 根据题目需求移动指针，有移动小的那方的
题目链接
有点类似于有效的字母异位词
也是给你两个字符串,判断第一个字符串能否由第二个字符串的字母组成
自己想到的是以空间换时间,建一个数组,26个英文字母,的然后看两个字符串所对应的有值的位置是不是一样.
其实在本题的情况下，使用map的空间消耗要比数组大一些的，因为map要维护红黑树或者哈希表，而且还要做哈希函数，是费时的！数据量大的话就能体现出来差别了。 所以数组更加简单直接有效！
其实让我我根本想不到map
class Solution {
public:
bool canConstruct(string ransomNote, string magazine) {
int res[26]={0};//别忘了一开始对数组所有元素赋0值!!!
for(int i=0;i<magazine.size();i++){
res[magazine[i]-'a']++;//magazine 中的每个字符只能在 ransomNote 中使用一次。
}
for(int i=0;i<ransomNote.size();i++){
res[ransomNote[i]-'a']--;
if(res[ransomNote[i]-'a']<0)
return false;
}return true;
}
};
`
暴力解法
```cpp
class Solution {
public:
bool canConstruct(string ransomNote, string magazine) {
//暴力解法，从头对两个字符串的字符，如果magazine里有ransomNote里需要的字符，就删去ran里的这个字符，最后如果ran的字符串为空，则返回true
for(int i=0;i<magazine.size();i++){
for(int j=0;j<ransomNote.size();j++){
if(magazine[i]==ransomNote[j]){
ransomNote.erase(ransomNote.begin()+j);//学学如何移除容器指定位置的元素
break;//别忘了跳出这个循环，因为对应于magezine的这个字符也不能再匹配了
} }}
if(ransomNote.empty())return true;
else return false;
}
};
15. 三数之和
-
- 根据题目需求移动指针，有移动小的那方的
题目链接
就先看懂的指针法，哈希法的去重有点麻烦，
双指针法：
连续三个一样的要去重。
其中 j > i + 2 的判断是为了保证b至少与a和a的下一个数构成了一个三元组。而 nums[j] == nums[j-1] && nums[j-1] == nums[j-2] 表示b与它前面的两个数相等，则跳过该数，这就是对b的去重操作。
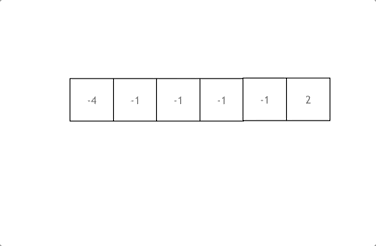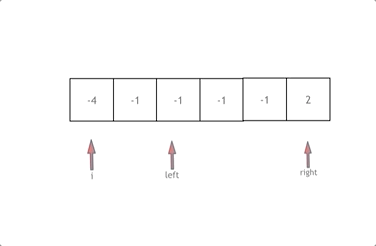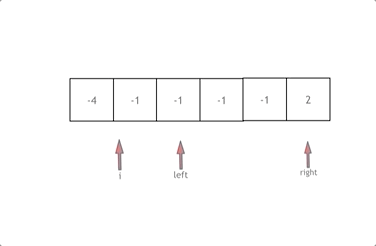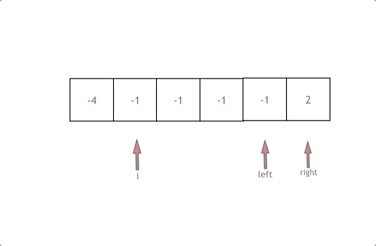一个for 循环，里面有两个while，有点类似于快排，但是每个指针都要有去重的思路。
根据题目需求移动指针，有移动小的那方的
那个移指针的，让我想到了408 的那个，
从三个升序数组里各区一个数，分别为a,b,c，找到一组a，b，c使得|a-b|+|b-c|+|a-c|的值最小，
思路是三个指针，分别代表三个数组里的a,b,c 的下标，在一个while循环里，条件是三个指针的都没到数组的尽头，然后进行判断，每次移动那个最小的数，往后移，因为只有最小的数往后移才会缩短它与其他数的区别，每次用一个取最小值的函数来取出每次移动后 的最小值，（与现有值和新出的差值的比较。）
push_back怎么用，把元素插入到数组末尾，
result.push_back(vector{元素})；
先是圆括号，容器<元素类型>大括号内是数组元素。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>>result;//声明多维数组的方法
sort(nums.begin(),nums.end());
//开始遍历数组
for(int i=0;i<nums.size();i++){
if(nums[0]>0)return result;//这个函数让返回的是个多维数组,所以一开始得声明一个多维数组.
//开始去重
if(i>0&&nums[i]==nums[i-1])continue;//别忘了i>0这个条件,因为他这个得等到第一个元素已经匹配完了才去重.
int left=i+1;
// int right=nums.end();不对,说明它们最终会将得到的迭代器作为函数的返回值反馈回来
//说明end()返回的是迭代器
int right =nums.size()-1;
while(left<right){
if(nums[i]+nums[left]+nums[right]<0)left++;
else if(nums[i]+nums[left]+nums[right]>0)right--;
else{
result.push_back(vector<int>{nums[i],nums[left],nums[right]});
//接下来开始去重:当前与后一个比较,若相同,则直接就指向下一个
while(left<right&&nums[right]==nums[right-1])right--;
while(left<right&&nums[left]==nums[left+1])left++;
//一直到不同的时候,确保不同,上面两个循环所停留的值还是相同的值
right--;
left++;
}
}
}//自己最后总爱忘记返回值
return result;
}
};
三树之和的哈希的解法难点就是在去重上，对b的去重。
i的去重是关于i会有重复的，j的去重是关于j有重复的，都是在凑出三数之和的情况下搞出来的。
哈希就是要比双指针多考虑一个j的去重，这个一般不符合大多数人的思维，因为大多数人都是直接整个算法就给问题解决了，而不是去自己试验堵细节。
这哪能堵得全。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>>result;
//先排序，输出要求是一个数不能用多次，不计较输出顺序，但是三元组不能有相同的
sort(nums.begin(),nums.end());
for(int i=0;i<nums.size();i++){
if(nums[i]>0)return result;
if(i>0&&nums[i]==nums[i-1])continue;
unordered_set<int> set;
for(int j=i+1;j<nums.size();j++){
//对b的去重在这里是难点。
if(j>i+2&&nums[j]==nums[j-1]&&nums[j-1]==nums[j-2])continue;
//这个去重是为了解决-4，2，2，2这种情况，即右边的数存在符合的情况但多了。
int c=0-(nums[i]+nums[j]);
if(set.find(c)!=set.end()){
result.push_back({nums[i],nums[j],c});//匹配了就插入到结果数组里，然后这个数就不能再匹配了，得把这个数去掉，
//究竟是去掉哪里的数呢，是set里的
set.erase(c);//三元组元素c去重。
}else set.insert(nums[j]);//未匹配上就插入set里，等待新的j与i之和来匹配。
}
}return result;}
};
18. 四数之和
-
- 根据题目需求移动指针，有移动小的那方的
题目链接
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>>result;//先建立一个数组
//然后排序
sort(nums.begin(),nums.end());
//进入循环
for(int i=0;i<nums.size();i++){
//一级剪枝,不是只对数组的第一个数，而是对最外层循环的i指向的数去重
if(nums[i]>target&&nums[i]>=0)break;//=可以忽略
//一级去重
if(i>0&&nums[i]==nums[i-1])continue;
//开始进入二重循环
for(int j=i+1;j<nums.size();j++){
//二级剪枝,可以改成nums[j]>0
if(nums[i]+nums[j]>target&&nums[j]+nums[i]>=0)break;
//二级去重
if(j>i+1&&nums[j]==nums[j-1])continue;
int left=j+1;
int right=nums.size()-1;
while(right>left){//看题目里数的范围，在10的9次方上
if((long)nums[i]+nums[j]+nums[left]+nums[right]>target)right--;
else if((long)nums[i]+nums[j]+nums[left]+nums[right]<target)left++;
else{
result.push_back({nums[i],nums[j],nums[left],nums[right]});
//去重
while(right>left&&nums[right]==nums[right-1])right--;
while(right>left&&nums[left]==nums[left+1])left++;
right--;
left++;
}
}
}
}
return result;
}
};
哈希表的经典题目：454.四数相加II
相对于本题简单很多，因为本题是要求在一个集合中找出四个数相加等于target，同时四元组不能重复。
而454.四数相加II
(opens new window)是四个独立的数组，只要找到A[i] + B[j] + C[k] + D[l] = 0就可以，不用考虑有重复的四个元素相加等于0的情况，所以相对于本题还是简单了不少