力扣每日一题

T1 1606 找到处理最多请求的服务器

题意&题解

       ~~~~~~       这道题是有k个服务器在同时工作，关键在于要读清楚题意。题目是说有n个任务依次到达，每个任务完成需要一段时间。任务如何分配给服务器，是有一个固定的策略：
       ~~~~~~       当然任务编号是i，那么倘若i%k这台服务器此时空闲，就把任务交给它，否则就接着向后查找一个空闲的服务器，注意服务器之间的关系可以当成一个环。
       ~~~~~~       通过分析可以知道，其实就是在做一个查询，查询(i%k,k-1)这个区间内第一个满足任务结束时间小于当前任务到达时间的服务器。
       ~~~~~~       这个查询可以直接做线段树二分，但是写起来有些麻烦。
       ~~~~~~       其实可以通过三个小根堆来实现。lef和rig这两个小根堆分别存储编号小于i%k的服务器和大于i%k的服务器。work小根堆存储的是正在工作中的服务器。
       ~~~~~~       但是因为有环，所以需要一个f来翻转：
       ~~~~~~               ~~~~~~       当f=0的时候，rig存的是编号大于等于i%k的服务器；
       ~~~~~~               ~~~~~~       当f=1的时候，lef存的是编号大于等于i%k的服务器。
       ~~~~~~       每当来了一个任务时，先把work中在arrival[i]时刻已经完成任务的服务器从work中弹出来，并加入到lef或rig中。
       ~~~~~~       然后根据f，找到离i%k最近的满足条件的服务器编号，将其加入到work中。
       ~~~~~~       倘若找不到，这个任务就搁置了。
       ~~~~~~       任务结束后，更新一下lef和rig。同时根据情况更新一下f。

代码

class Solution {
public:
    vector<int> busiestServers(int k, vector<int>& arrival, vector<int>& load) {
        vector<int>num(k,0);
        priority_queue<int> lef,rig;
        priority_queue<pair<int,int> >work;
        for(int i=0;i<k;i++) rig.push(-i);
        int n=arrival.size();
        bool f=0;
        //f=0代表编号大于等于i%k的在rig，否则代表在lef
        for(int i=0;i<n;i++){
            if(work.size()){
                while(work.size()){
                    int id=work.top().second;
                    int lasttime=-work.top().first;
                    if(lasttime<arrival[i]){
                        work.pop();
                        if(f==0){
                            if(id>=i%k) rig.push(-id);
                            else lef.push(-id);
                        }else{
                            if(id>=i%k) lef.push(-id);
                            else rig.push(-id);
                        }
                    }else{
                        break;
                    }
                }
            }
            if(f==0){
                if(rig.size()){
                    int id=-rig.top();
                    num[id]++;
                    work.push(make_pair(-(arrival[i]+load[i]-1),id));
                    rig.pop();
                }else if(lef.size()){
                    int id=-lef.top();
                    num[id]++;
                    work.push(make_pair(-(arrival[i]+load[i]-1),id));
                    lef.pop();
                }
            }else{
                if(lef.size()){
                    int id=-lef.top();
                    num[id]++;
                    work.push(make_pair(-(arrival[i]+load[i]-1),id));
                    lef.pop();
                }else if(rig.size()){
                    int id=-rig.top();
                    num[id]++;
                    work.push(make_pair(-(arrival[i]+load[i]-1),id));
                    rig.pop();
                }
            }
            if(f==0){
                while(rig.size()){
                    int id=-rig.top();
                    if(id<=i%k){
                        rig.pop();
                        lef.push(-id);
                    }else break;
                }
            }else{
                while(lef.size()){
                    int id=-lef.top();
                    if(id<=i%k){
                        lef.pop();
                        rig.push(-id);
                    }else break;
                }
            }
            if(i%k==k-1){
                f=!f;
            }
        }
        vector<int>ans;
        int maxx=0;
        for(int i=0;i<k;i++){
            maxx=max(maxx,num[i]);
        }
        for(int i=0;i<k;i++){
            if(num[i]==maxx) ans.push_back(i);
        }
        return ans;
    }
};

T2 1044 最长重复字串

题意

       ~~~~~~       题意很简单，就是让你找到一个最长的子串，使得这个子串至少出现了两次。

题解

       ~~~~~~       n是3e4，注意到一个性质，答案具有连续性，就是说假如长度L满足条件，那么L-1一定满足。因此可以二分长度，然后判断是否满足条件。如何判断呢？直接O(n)遍历每一个长度为mid的字符串，记录出现次数即可。这个可以用hash来O(1)实现。计数用map实现了，但TLE，因此改用unordered_map。单哈会被卡，采用双哈。

代码

class Solution {
public:
    string longestDupSubstring(string s) {
        const long long p1=998244353,p2=1e9+7;
        int len=s.size();
        vector<long long>sum1,sum2,po1,po2;
        sum1.push_back(0);
        sum2.push_back(0);
        po1.push_back(1);
        po2.push_back(1);
        for(int i=1;i<=len;i++){
            long long tmp=sum1[i-1]*31%p1+s[i-1]-'a';
            tmp%=p1;
            sum1.push_back(tmp);
        }
        for(int i=1;i<=len;i++){
            long long tmp=sum2[i-1]*131%p2+s[i-1]-'a';
            tmp%=p2;
            sum2.push_back(tmp);
        }
        for(int i=1;i<=len;i++){
            po1.push_back(po1[i-1]*31%p1);
            po2.push_back(po2[i-1]*131%p2);
        }
        int l=0,r=len-1;
        unordered_map<long long,int>num1,num2;
        int lef;
        while(l<r){
            int mid=(l+r+1)/2;
            bool flag=0;
            for(int i=1;i<=len;i++){
                int L=i,R=L+mid-1;
                if(R>len) break;
                long long tmp1=sum1[R]-po1[mid]*sum1[L-1]%p1;
                tmp1=(tmp1%p1+p1)%p1;
                num1[tmp1]++;
                long long tmp2=sum2[R]-po2[mid]*sum2[L-1]%p2;
                tmp2=(tmp2%p2+p2)%p2;
                num2[tmp2]++;
                if(num1[tmp1]>1&&num2[tmp2]>1){
                    lef=L;
                    flag=1;break;
                }
            }
            if(flag){
                l=mid;
            }else{
                r=mid-1;
            }
            num1.clear();
            num2.clear();
        }
        if(l>0){
            string a;
            //cout<
            for(int i=lef-1;i<lef+l-1;i++) a+=s[i];
            return a;
        }
        return "";
    }
};

T3 587 安装栅栏

题意

        ~~~~~~~        给定n个点的坐标，希望围一个栅栏，使得栅栏能包括所有的点，且栅栏长度尽可能小。

题解

       ~~~~~~       这类问题，就是经典的求最小周长，所以是凸包模板题，求一个凸包即可。求凸包采用Andrew算法，通过单调队列维护一个下凸壳和上凸壳。注意凸壳的性质是，以逆时针的顺序访问所有点，向量是在不断向左旋转，否则就会产生凹陷。这个判断使用叉乘判断是否小于0即可，小于0就代表产生了凹陷。

代码

class Solution {
public:
    static bool cmp(const vector<int>& a,const vector<int>& b){
        return (a[0]<b[0]||(a[0]==b[0]&&a[1]<b[1]));
    }
    int calc(vector<int> a,vector<int> b,vector<int> c){
        int X1=b[0]-a[0];
        int Y1=b[1]-a[1];
        int X2=c[0]-b[0];
        int Y2=c[1]-b[1];
        return X1*Y2-X2*Y1;
    }
    vector<vector<int>> outerTrees(vector<vector<int>>& trees) {
        int n=trees.size();
        vector<int>s;
        vector<bool>vis(n,0);
        int top=0;
        sort(trees.begin(),trees.end(),cmp);
        for(int i=0;i<n;i++){
            while(top>=2&&calc(trees[s[top-2]],trees[s[top-1]],trees[i])<0){
                vis[s[top-1]]=0;
                top--;
                s.pop_back();
            }
            s.push_back(i);
            if(i!=0)
            vis[i]=1;
            top++;
        }
        int tmp=top;
        for(int i=n-1;i>=0;i--){
            if(!vis[i]){
                //cout<
                while(top>tmp&&calc(trees[s[top-2]],trees[s[top-1]],trees[i])<0){
                    vis[s[top-1]]=0;
                    top--;
                    s.pop_back();
                }
                s.push_back(i);
                vis[i]=1;
                top++;
            }
        }
        vector<vector<int>>ans;
        for(int i=0;i<n;i++) if(vis[i]) ans.push_back(trees[i]);
        return ans;
    }
};

T4 72 编辑距离

题意

        ~~~~~~~        给定两个字符串a和b，问最少经过多少次操作可以使a变成b。操作有三种：1、删除一个字符；2、插入一个字符；3、替换一个字符。

题解

        ~~~~~~~        这就是一个很经典的两个字符串匹配问题，直接n*m的dp递推即可。只不过有一个插入和删除操作而已，只需要单独分析一下就行。$dp[i][j]$表示a串的前i个匹配到了b串的前j个需要多少次操作，分析可得以下式子：
$$if(a[i]==b[j])dp[i][j]=min(dp[i][j],dp[i-1][j-1])$$
下面是替换
$$dp[i][j]=min(dp[i][j],dp[i-1][j-1]+1)$$
下面是删除
$$dp[i][j]=min(dp[i][j],dp[i-1][j]+1)$$
下面是插入
$$dp[i][j]=min(dp[i][j],dp[i][j-1]+1)$$
        ~~~~~~~        需要注意的一个点是，不要忘了特殊情况的初始化，即a串是空串或者b串是空串的答案。

代码

class Solution {
public:
    int minDistance(string word1, string word2) {
        int n=word1.size(),m=word2.size();
        vector<vector<int>>dp(n+1,vector<int>(m+1,1e9));
        dp[0][0]=0;
        for(int i=1;i<=n;i++) dp[i][0]=i;
        for(int i=1;i<=m;i++) dp[0][i]=i;
        for(int i=1;i<=n;i++){
            dp[i][0]=i;
            for(int j=1;j<=m;j++){
                if(word1[i-1]==word2[j-1]){
                    dp[i][j]=min(dp[i][j],dp[i-1][j-1]);
                }
                dp[i][j]=min(dp[i][j],dp[i-1][j]+1);//删除
                dp[i][j]=min(dp[i][j],dp[i][j-1]+1);//添加
                dp[i][j]=min(dp[i][j],dp[i-1][j-1]+1);//替换
            }
        }
        return dp[n][m];
    }
};

T5 84 柱状图中最大的矩形

题意

       ~~~~~~       给定n个数，代表一个柱形图。求能在柱状图中找到的最大的矩形面积，$n<=1e5$

题解

       ~~~~~~       一个比较容易得到的思路是，因为面积要最大，所以矩阵的高一定是n个数当中的某一个。我们就依次假设每一个数作为高，那就要尽可能得向左向右扩展，这样才能面积更大。所以问题转化为了，一个数a[i]，向左向右最多能延伸多长，延伸的过程中不能遇到小于它的数。我们再转化一下，想知道能往左延伸的最长长度，其实就是从右往左找到第一个小于它的数，然后这俩数的距离就是长度。
       ~~~~~~       上述问题其实可以直接没脑子的套线段树二分做，复杂度也过关。不过其实这道题是静态的，可以用单调栈解决。只需要维护一个严格单调递增的栈即可，然后当前i要入栈，那么要把栈中所有大于它的全部弹出去，最后栈顶就是第一个小于它的数。至于向右的，再反着扫一遍就行了。

代码

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n=heights.size();
        vector<int>s;
        vector<int>lef(n+1,1),rig(n+1,1);
        int top=0;
        for(int i=0;i<n;i++){
            while(top&&heights[s[top-1]]>=heights[i]){
                s.pop_back();
                top--;
            }
            if(top==0) lef[i]=i+1;
            else lef[i]=i-s[top-1];
            top++;
            s.push_back(i);
        }
        top=0;
        while(s.size()) s.pop_back();
        for(int i=n-1;i>=0;i--){
            while(top&&heights[s[top-1]]>=heights[i]){
                s.pop_back();
                top--;
            }
            if(top==0) rig[i]=n-i;
            else rig[i]=s[top-1]-i;
            top++;
            s.push_back(i);
        }
        int ans=0;
        for(int i=0;i<n;i++){
            int l=lef[i]+rig[i]-1;
            ans=max(ans,l*heights[i]);
        }
        return ans;
    }
};

T6 某团笔试题

题意

       ~~~~~~       有n个人站成一排，编号从1到n。接下来有m个关系描述，是以点对的形式(ai,bi)，表示ai和bi互相不认识。问有多少个连续的子区间，区间内的所有人两两互相认识。$n<=500000$

题解

       ~~~~~~       考虑线性做法。注意到当有一个点对(l,r)互相不认识以后，那么对于所有左端点小于等于l，右端点大于等于r的区间，均不再符合条件。但直接这样计数会出现重复。考虑到所有的区间等于$\sum ans[i]$,其中$ans[i]$是以i为左端点的区间。我们维护一个数组$Min$，$Min[i]$表示从i向右走，保证互相认识的前提下能走到的最远距离。最初$Min[i]$都为$n$。对于m个描述，均令$Min[ai]=min(Min[ai],bi)$，注意保证$ai<bi$。然后我们从右往左扫，每次使$Min[i]=min(Min[i],Min[i+1])$。维护出来Min数组以后，答案就很容易算出来了。

T7 某团笔试题

题意

       ~~~~~~       一条路，长为n，宽为2。路上有n个怪，每个怪可能宽度是1，那么就可以绕过它。也有的怪宽度为2，就必须打败它。打败一个怪的前提是你当前武力值大于等于怪的武力值。当打死这个怪以后，武力值会累加上等同于怪的武力值。起初有k的武力值。问：最少需要打几个怪才能到达终点？$n<=50000,k<=1e9$

题解

       ~~~~~~       贪心一下，最开始能跳过的怪都跳过，等遇到必须要打的怪的时候，如果武力值不够，那么最优策略应该是找到之前跳过的怪中武力值小于等于当前武力值的最大武力值的怪，把它打了。若仍无法通过，那就接着找。这个过程用set模拟很方便。每遇到一个宽度为1的怪，就插入到set里。遇到一个宽度为2的怪，就while循环，不断lower_bound找到符合条件的最大的武力值。

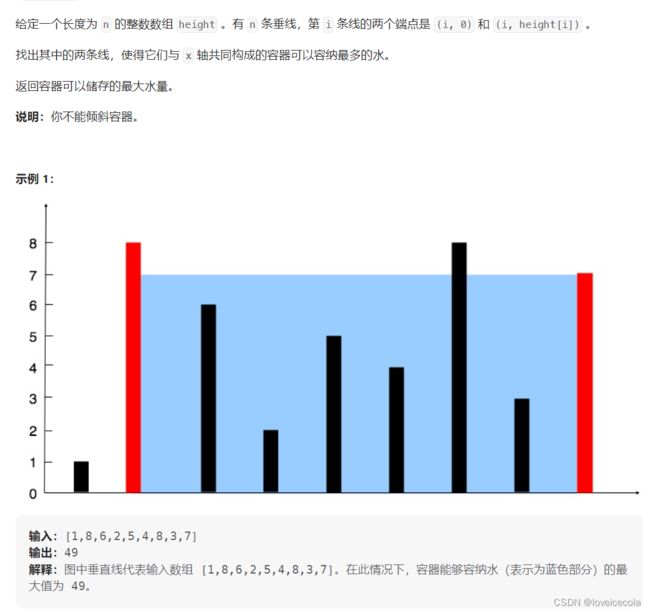
T8 力扣 盛最多水的容器

题解

       ~~~~~~       虽然是中等难度，但还挺巧妙的一个思路。假定我们目前选取的是(i,j)这个点对形成的容器。那么接下来对于左端点大于等于i，右端点小于等于j的所有点对，我们需要找到一个最大值。分析一下，当前的容量$=min(h[i],h[j])\ast (j-i)$。假设$h[i]<h[j]$，那么我们将$j--$，容量一定是减小的。因为$min(h[i],h[j])>=min(h[i],h[j-1])$。因此我们只可能移动i，才有机会增大容量。最开始令$i=0，j=len-1$。当i和j碰到一起的时候，我们也对所有可能构成最大容量的点对遍历了一遍。

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}
func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}
func maxArea(height []int) int {
    ans := 0
    i, j := 0, len(height) - 1
    for i < j {
        ans = max(ans, min(height[i], height[j]) * (j - i))
        if height[i] < height[j] {
            i++
        } else {
            j--
        }
    }
    return ans
}

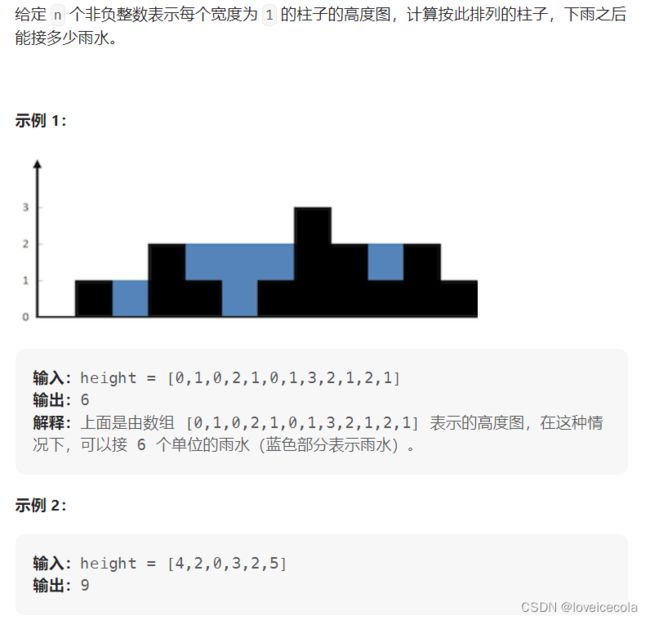
T9 力扣 接雨水

题目

分析

       ~~~~~~       注意到能接到雨水的一定是凹进去的。考虑维护一个单调递减的单调栈，当到达第i个点时，需要把栈中的所有小于等于height[i]的点都弹出去，且弹出去的过程当中可以接雨水。需要注意的细节是，能接雨水有两个条件：1、当前栈顶是低于height[i]的；2、栈顶的左边还有一个高于它的节点，形成了凹，才有水。

代码

func min(i, j int) int {
    if i < j {
        return i
    } else {
        return j
    }
}
func trap(height []int) int {
    ans := 0
    sta := []int {}
    for i, h := range height {
        if len(sta) == 0 || h < height[sta[len(sta) - 1]] {
            sta = append(sta, i)
        } else {
           // for _, id := range sta {
              //  fmt.Print(id, height[id], " ")
            //}
            fmt.Println("");
            for len(sta) > 1 && height[sta[len(sta) - 1]] <= h {
                low := height[sta[len(sta) - 1]]
                width := (i - sta[len(sta) - 2] - 1)
                //fmt.Println(low, min(h, height[sta[len(sta) - 2]]))
                ans += (min(h, height[sta[len(sta) - 2]]) - low) * width
                sta = sta[0 : len(sta) - 1]
            }
            for len(sta) > 0 && height[sta[len(sta) - 1]] <= h {
                sta = sta[0 : len(sta) - 1]
            } 
            sta = append(sta, i)
        }
    }
    return ans
}

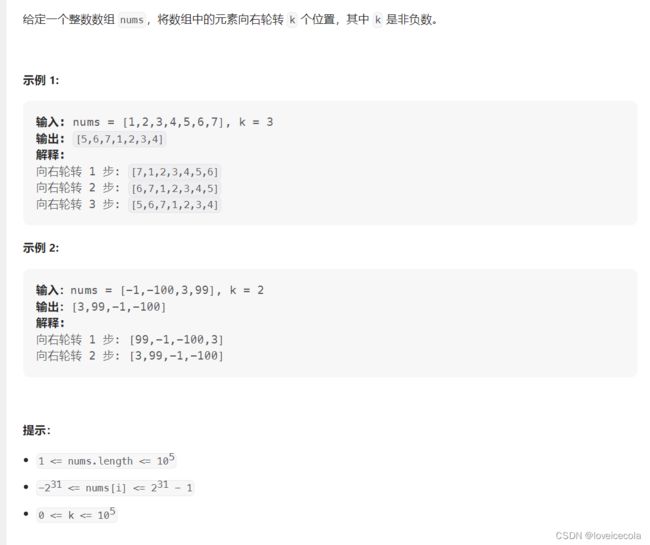
T10 力扣 轮转数组

分析

       ~~~~~~       这道题本身并没有什么难度，我们另开一个数组，很轻松就把数组轮转了。主要考虑的是进阶做法，能否以O(1)的空间复杂度实现？且多种做法。
       ~~~~~~       先说一个比较容易想到的思路：很容易总结出来的规律，轮转$k$次就相当于每一个位置上的数向右平移$k$下，也就是从$i$跑到$(i+k)modn$. 假设我们现在从i=0开始，它的值要放在i+k，然后i+k的值又要放在i+2*k里，一直向后。什么时候会停下来？只要遇到一个之前访问过的节点，就会停下来了。这时候恰好完成了一次轮询，相当于构成了一个环，这个环上所有的值都向后移动了一次，因此只需要O(1)的复杂度。时间复杂度很明显是线性的，因为每个下标只会被访问一次。如果要严格证明为什么这样可以访问完所有的节点，会设计到数论的一些知识。这里就不讨论了。
       ~~~~~~       另外一个更加妙的思路。我们知道对一个数组进行翻转操作，其实只需要O(1)的空间复杂度的。因为翻转只需要把所有对应的点对就行swap就行。我们再根据例子找规律，发现经过k次轮询后，其实等价于后面的k个数放在了头部，前面的n-k个数整体后移。我们先将整个数组进行翻转，这样后面的k个数就到达了头部。只不过目前处于倒序，我们再把前k个数进行整体翻转，把后n-k个数也整体翻转，这样就做完了。

func rotate(nums []int, k int)  {
    k %= len(nums)
    mp := map[int]bool {}
    for i := 0; i < len(nums); i++ {
        now := i
        num := nums[i]
        for mp[(now + k) % len(nums)] == false {
            temp := nums[(now + k) % len(nums)]
            nums[(now + k) % len(nums)] = num
            num = temp
            mp[(now + k) % len(nums)] = true
            now = (now + k) % len(nums)
        }
    }
}

T11 力扣 缺失的第一个正整数

分析

       ~~~~~~       这题是真不好想，盯着屏幕杠了20分钟才有思路。缺失的第一个正整数，其实这玩意儿就是求mex。还好在学博弈论以及一些数据结构题目中接触过mex，知道一些性质。有$n$个数的话，mex其实一定是$[1,n+1]$中的某个数。这个很好证明，对于最差的情况就是$1$到$n$全部出现了一次，那么mex最大，是$n+1$，否则$1$到$n$中肯定有数没出现过，mex就是最小的它。基于这个思路，貌似我们只判断1到n的数有没有出现过就可以。但是这道题要求是常数级的额外空间。
       ~~~~~~       想了很久想到了原地hash。直接用nums数组当做我的hash数组。当遇到一个数$nums[i]$的时候，假如它属于$[1,n]$这个范围内，我就令$nums[nums[i]]=1$，代表这个数值出现过了。但是这样会引发一个问题，就是可能会覆盖掉原本下标是$nums[i]$的数，所以我们用一个循环不断轮询，类似上道题的轮询。与此同时还有一个问题，那就是这个表示出现过的$1$和初始数值的$1$产生了冲突。因此我们单独去考虑$1$有没有出现过。

代码

func firstMissingPositive(nums []int) int {
    flag := false
    for i, num := range nums {
        if num == 1 {
            flag = true
            nums[i] = 0
        }
    }
    for i, num := range nums {
        //nums[i] = 0
        if num <= len(nums) {
            for num - 1 > i && num <= len(nums) {
                tmp := nums[num - 1]
                nums[num - 1] = 1
                num = tmp
            }
            if num - 1 <= i && num - 1 >= 0 {
                nums[num - 1] = 1
            }
        }
    }
    if flag == false {
        return 1
    } else {
        for i := 1; i < len(nums); i++ {
            if nums[i] != 1 {
                return i + 1
            }
        }
        return len(nums) + 1
    }
}

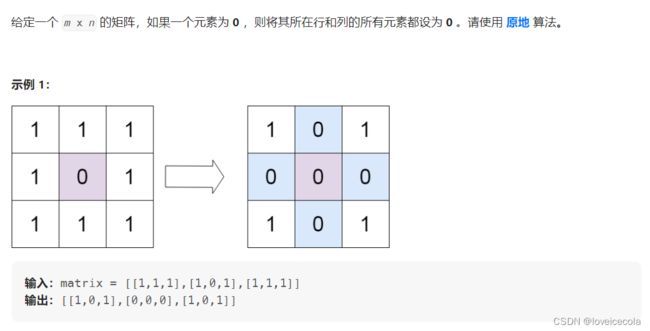
T12 力扣 矩阵置零

分析

       ~~~~~~       这里我们直接考虑进阶的，仅使用常量空间。有个小技巧就是，假如遇到了$nums(i,j)==0$，我们知道要将第$i$行和第$j$列全部置0.但我们为了不影响后面的点，必须把这个置零操作延缓一下，也就是保存下来。但我们只能使用常量的额外空间。注意到，假设第$i$行需要置0，那么我们可以令$num(i,0)=0$，代表第$i$行要置0；假如第$j$列需要置零，我们令$num(0,j)=0$，代表第$j$列需要置0.也就是说我们原地利用了$num$这个数组。需要注意的是，$num(0,0)=0$代表的意思会混淆。因此对于第零行和第零列，我们单独用两个$flag$变量也判断。

代码

func setZeroes(matrix [][]int)  {
    flag1, flag2 := false, false
    for i := 0; i < len(matrix); i++ {
        for j := 0; j < len(matrix[i]); j++ {
            if matrix[i][j] == 0 {
                matrix[0][j] = 0
                matrix[i][0] = 0
                if j == 0 {
                    flag2 = true
                }
                if i == 0 {
                    flag1 = true
                }
            }
        }
    }
    for j := 1; j < len(matrix[0]); j++ {
        for i := 1; i < len(matrix); i++ {
            if matrix[0][j] == 0 {
                matrix[i][j] = 0
            }
        }
    }
    for i := 1; i < len(matrix); i++ {
        for j := 1; j < len(matrix[i]); j++ {
            if matrix[i][0] == 0 {
                matrix[i][j] = 0
            }
        }
    }
    if flag1 == true {
        for j := 0; j < len(matrix[0]); j++ {
            matrix[0][j] = 0
        }
    }
    if flag2 == true {
        for i := 0; i < len(matrix); i++ {
            matrix[i][0] = 0
        }
    }
}

T13 力扣 搜索二维矩阵 II

题目

分析

       ~~~~~~       好妙的一道题。直接在每一行二分复杂度$O(mlogn)$，但倘若要求为线性，就得好好利用题目的性质了。注意到二分其实只利用了每一行递增的性质，没利用到同时每一列也是递增的性质。我们以左下角为不变的边界，右上角为变动的边界。最初右上角是$x=0,y=n-1$.当$$m[x][y]<target,说明当前第x行剩下的所有数都小于target，令x++$$
$$m[x][y]>target,说明第y列剩下的所有数都大于target，令y--$$
$$m[x][y]==target,找到一个目标值，令x++,y--，继续找$$
       ~~~~~~       时间复杂度$O(n+m)$

代码

func searchMatrix(matrix [][]int, target int) bool {
    m, n := len(matrix), len(matrix[0])
    x, y := 0, n - 1
    flag := false
    for {
        if x >= m {
            break
        }
        if y < 0 {
            break
        }
        if matrix[x][y] < target {
            x++
        } else if matrix[x][y] > target {
            y--
        } else {
            flag = true
            x++
            y--
        }
    }
    return flag
}

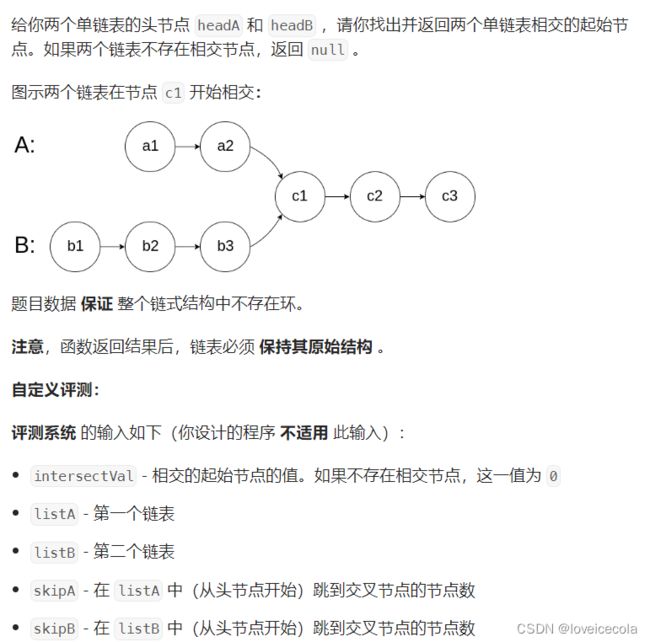
T14 力扣 相交链表

题目

分析

       ~~~~~~       最开始没想到进阶的解法，看了题解最开始还看迷糊了，后面理解题解的意思了，以为挺妙的。后来和别人说这道题的时候突然意识到，题解太绕了所以第一遍没看明白。其实没有那么麻烦。这个单向链表本质上就是有向图的一条链。两条链表产生了相交，那其实就相当于一棵树，求第一个产生交叉的节点，其实就是求lca。求lca应该先把深度统一，然后再同步往上跳。因此首先我们要摸清楚两个头结点的深度，所以需要分别遍历一遍两条链表，然后求得头结点的深度。之后将深度大的先向上跳到深度同步。再一起往下跳即可。

T15 力扣 链表反转

分析

       ~~~~~~       反转链表这种题对我这个不经常写链表的人，实在有点不友好，还得加练。迭代的思路就是，遇到一个当前节点，它的指针应该从指向下一个节点变成指向上一个节点。因此我们首先需要有一个中间变量来存储pre节点。其次，在我们将当前节点的指针指向pre前，还需要先记录一下下一个节点，防止其被覆盖而丢失。
       ~~~~~~       至于递归写法，一定要要问题的划分定义清楚。假设我们的函数reverse就是将以当前head为头结点的链表反转并返回新的头结点。那么我们可以先递归处理以head.Next为头结点的链表，然后将这个head.Next的Next指向现在的head。然后要返回的头结点自然也等价于以head.Next为头结点的链表反转以后的新头结点。

代码

func reverseList(head *ListNode) *ListNode {
    var pre *ListNode = nil
    cur := head
    for cur != nil {
        next := cur.Next
        cur.Next = pre
        pre = cur
        cur = next
    }
    return pre
}

func reverseList(head *ListNode) *ListNode {
    if head == nil || head.Next == nil {
        return head
    }
    newHead := reverseList(head.Next)
    head.Next.Next = head
    head.Next = nil
    return newHead
}

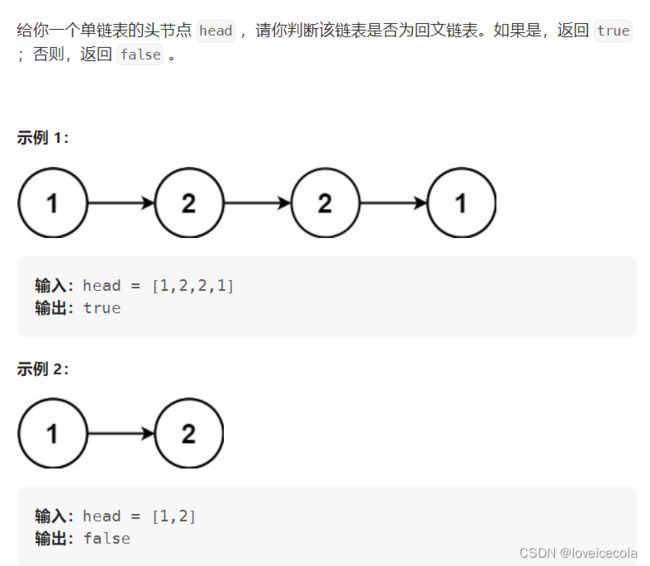
T16 力扣 回文链表

题目

分析

       ~~~~~~       直接考虑进阶版，时间复杂度$O(m+n)$，空间复杂度$O(1)$。可以先扫描一遍得到链表长度，然后再次扫描，在长度为一半的地方截断，变成两个链表。然后将第一个链表反转，然后for循环比对是否相同即可。链表反转就直接用上道题的迭代反转法。

代码

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func isPalindrome(head *ListNode) bool {
    l := 0
    cur := head
    for cur != nil {
        l++
        cur = cur.Next
    }
    l1 := 0
    cur = head
    var head1 *ListNode
    //fmt.Println(l)
    for cur != nil && l1 < l / 2 {
        l1++
        if l1 == l / 2 {
            if l % 2 == 0 {
                head1 = cur.Next
                //fmt.Println(head1.Next.Val)
            } else {
                head1 = cur.Next.Next
            }
            //fmt.Println(cur.Val)
            cur.Next = nil
        }
        cur = cur.Next
    }
    var pre *ListNode = nil
    cur = head
    for cur != nil {
        next := cur.Next
        cur.Next = pre
        pre = cur
        //fmt.Println(cur.Val)
        cur = next
    }
    head = pre
    //fmt.Println(head1.Val)
    cur = head
    cur1 := head1
    for cur != nil && cur1 != nil {
        //fmt.Println(cur.Val,cur1.Val)
        if cur.Val != cur1.Val {
            return false
        }
        cur = cur.Next
        cur1 = cur1.Next
    }
    return true
}