CUDA入门之利用GPU寻找一组数据中最大的k个元素(一)
参加CUDA On Arm Platform 线上夏令营学习笔记(四)
- 代码部分
- 讲解部分
- 反思优化
代码部分
#include 讲解部分
在介绍GPU寻找一组数据中最大的k个元素之前,首先要介绍一个非常好用的工具函数__device__ __host__ void insert_value(int* array, int k, int data),再次感谢Ken老师的帮助。
__device__ __host__ void insert_value(int* array, int k, int data)
{
/*
* 感谢Ken老师提供的函数
* 作用:判定插入的值是否为目标数组中非重复的最大的k个元素之一,若是,则插入恰当位置(从大到小)并保证其余元素的相对位置不发生改变。
* array 被插入的目标数组
* k 目标数组中需要按顺序排列的元素个数
* data 插入的值
*/
for (int i = 0; i < k; i++)
{
//重复则不需要插入,直接返回
if (array[i] == data)
{
return;
}
}
//因为目标数组最大的k个元素默认再最前面且按照从大到小的顺序排列,所以当插入的值小于第数组中第k个元素即array[k-1]时,即表面插入值并非该数组中最大的k个元素之一。
if (data < array[k - 1])
return;
//经过前面判断,得出插入值符合条件,所以将值插入恰当位置(从大到小)
for (int i = k - 2; i >= 0; i--)
{
if (data > array[i])
array[i + 1] = array[i];
else {
array[i + 1] = data;
return;
}
}
array[0] = data;
}
相信大家通过作者的注释已经可以看懂这个代码,该函数的作用就是判定插入的值是否为目标数组中非重复的最大的k个元素之一,若是,则插入恰当位置(从大到小),并保证其余元素的相对位置不发生改变。
接下来就是介绍今天的重头戏:__global__ void top_k(int* input, int length, int* output, int k)
注意作者在这里的整体思想是——每个线程只干两件事:
- 把这个线程读入的数据中最大的k个值按照顺序写入shared mem
- 与其他线程合作,求出它所在的block内shared mem中所有数据的k个最大值,并写入输出向量
由于作者使用的设备为nano,该设备的特点为同一内存,因此不需要将数据拷入到GPU中,而是直接申请内存即可。
__managed__ int source_array[N];
__managed__ int _1pass_results[topk * GRID_SIZE];
__managed__ int final_results[topk];
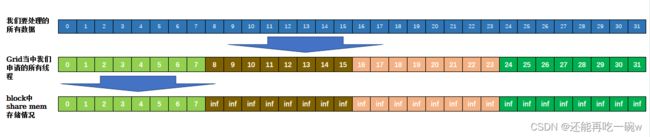
在第一次调用核函数时,其配置参数为<<<((N + BLOCK_SIZE - 1) / BLOCK_SIZE),BLOCK_SIZE>>>,所以申请的线程数大于或等于输入数据的元素个数,所以每个线程只读取一个数据,并将数据写入shared mem中,share mem的其余位置以INT_MIN代替,防止上溢。share mem存储如下图所示,由于图幅有限,以grid = 4 ,blocksize = 8,k = 4为例。
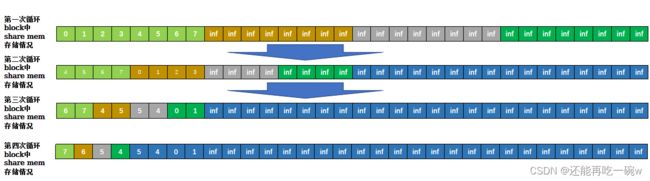
接下来便是执行for循环,与其他线程合作,求出它所在的block内shared mem中所有数据的k个最大值。首先便是两两线程对比,将一个线程中维护的k个最大的数值通过insert_value函数做对比,从2k个元素中挑选出k个最大的元素返回到一个线程中,因此,被对比的线程因为被合并而后续不需要再讨论,返回数据的线程则将得到的k个最大元素写入到share memory中。随着循环的进行,被实际使用的shared memory越来越小,从最大的BLOCKSIZE * k,到BLOCKSIZE /2 * k,再到BLOCKSIZE /4 * k,……,最后到1*k,循环结束。如下图所示。
for (int m = 0; m < topk; m++){
insert_value(top_array, topk, lich[topk * (threadIdx.x + i) + m]);
}
__syncthreads();
if (threadIdx.x < i){
for (int m = 0; m < topk; m++){
lich[topk* threadIdx.x + m] = top_array[m];
}
}
得到了一个block中最大的k个元素后,将其写入到输出向量中。(屎山代码,其实可以并行计算的,作者实在是懒得改了,留给后人了。)
if (blockIdx.x * blockDim.x < length){
if (threadIdx.x == 0){
for (int m = 0; m < topk; m++){
output[topk * blockIdx.x + m] = lich[m];
}
}
}
由于采用two-pass的方法,所以还需要调用一次核函数,为了保证输出向量只有k个元素,因此grid需要设定为1。
top_k << <GRID_SIZE, BLOCK_SIZE >> > (source_array, N, _1pass_results, topk);
top_k << <1, BLOCK_SIZE >> > (_1pass_results, topk * GRID_SIZE, final_results, topk);
而在第二次执行核函数时,因为其配置参数为<< <1, BLOCK_SIZE >> > ,所以可以发现申请的线程数远少于输入数据的元素个数,因此在单个线程读入数据时,每个线程并非只读入对应于该线程的一个元素,所以需要利用insert_value函数进行提取最大的k个值,不足k个的话用依旧使用INT_MIN补全,防止上溢。
for (int idx = threadIdx.x + blockDim.x * blockIdx.x; idx < length; idx += gridDim.x * blockDim.x)
{
insert_value(top_array, k, input[idx]);
}
其余步骤同第一次调用kernel,最终得到了输入数据中最大的k个元素,也同样是原始数据中最大的k个元素。
反思优化
作者在写这篇博客整理复盘这个topk求值时候有个思路,因为是采用two-pass的方法进行求解,但是第二次grid等于1时,申请的线程数其实是远小于输入数据的数量,这样在ken老师提供的insert_value函数会在最初赋值的时候调用很多次,如果多调用几次核函数,使最后一次就final的时候申请的线程数大于等于输入的数据,那么执行速度会更快吗?
后续如果有代码实现作者将重新开一篇文章来介绍。
当然其实还有更快的优化思路,就是kernel的求解算法修正,而且还有很大的修正空间,如果有空,同样也是再开一篇文章来介绍,顺便把原代码里面的屎山给消灭掉。