（数字图像处理MATLAB+Python）第十章图像分割-第三，四节：区域分割和基于聚类的图像分割

一：区域分割

区域分割：一般认为，同一个区域内的像素点具有某种相似性，如灰度、颜色、纹理等，区域分割即是根据特定区域与其他背景区域特性上的不同来进行图像分割的技术

• 区域生长
• 区域合并
• 区域分裂
• 区域合并分裂

（1）区域生长

A：原理

区域生长：是一种基于像素相似性的图像分割方法，旨在将具有相似特征的像素逐步合并成更大的区域。该方法从一个或多个种子像素开始，通过逐渐添加与当前区域相似的邻接像素，最终形成一系列连通的区域。区域生长方法适用于分割均匀且连续的区域，但在面对弱纹理、噪声或边界模糊等情况时可能效果不佳。算法步骤如下

• 选择种子点： 首先从图像中选择一个或多个种子像素作为起始点。通常情况下，种子点可以通过人工选择或者根据一些特定规则自动确定（可以是单个像素，也可以是包括若干个像素的子区域，根据具体问题，利用先验知识来选择）
• 定义相似性准则： 确定像素之间的相似性度量标准，如灰度值、颜色、纹理等。通常，选择与种子像素相似度高于某个阈值的邻接像素
• 种子扩展： 从种子点开始，根据相似性准则逐渐添加邻接像素到当前区域中。可以使用递归、队列等方式来扩展种子区域
• 判断停止条件： 在区域生长的过程中，需要定义停止条件，即什么情况下停止合并。常见的停止条件包括达到一定区域大小、相似性度量低于阈值等
• 迭代： 重复执行种子扩展和判断停止条件的过程，直到所有的区域都被完全分割出来

区域生长方法的优点是简单易用，可以在不需要预先训练的情况下应用于许多图像分割问题。然而，它对噪声、弱纹理和边界不清晰的情况较为敏感，可能会导致错误的合并或分割。为了克服这些问题，可以考虑引入更复杂的区域分割算法，如基于图割的方法、深度学习方法等，以获得更准确和稳定的分割结果

B：示例

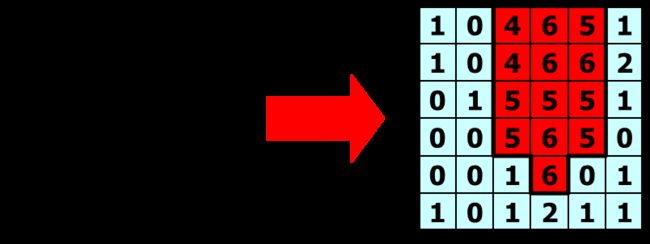
如下例

• 种子点：(2,2)
• 相似性准则：灰度值差小于2
• 邻域选择：4领域

C：程序

如下：对图像进行区域生长。交互式选取种子，生长准则采用“待测像素点与区域的平均灰度差小于40”，8邻域范围生长，停止生长条件为区域饱和

---

matlab实现：

clear,clc,close all;
Image=im2double(imread('lotus1.jpg'));
[height,width,channel]=size(Image);
if channel==3
    Image=rgb2gray(Image);
end
figure,imshow(Image);
% Image=[1 0 4 6 5 1;1 0 4 6 6 2;0 1 5 5 5 1;0 0 5 6 5 0;0 0 1 6 0 1;1 0 1 2 1 1];
% [height,width,channel]=size(Image);
% figure,imshow(Image);
[seedx,seedy,button] = ginput(1);
seedx=round(seedx);
seedy=round(seedy);
region=zeros(height,width);
region(seedy,seedx)=1;
region_mean=Image(seedy,seedx);
region_num=1;
flag=zeros(height,width);
flag(seedy,seedx)=1;
neighbor=[-1 -1;-1 0;-1 1;0 -1;0 1;1 -1;1 0;1 1];
for k=1:8
    y=seedy+neighbor(k,1);
    x=seedx+neighbor(k,2);
    waiting(k,:)=[y,x];
    flag(y,x)=2;
end

pos=1;
len=length(waiting);
while pos<len
    len=length(waiting);
    current=waiting(pos,:);
    pos=pos+1;
    pixel=Image(current(1),current(2));
    pdist=abs(pixel-region_mean);
    if pdist<40/255 
        region(current(1),current(2))=1;
        region_mean=region_mean*region_num+pixel;
        region_num=region_num+1;
        region_mean=region_mean/region_num;
        for k=1:8   
            newpoint=current+neighbor(k,:);
            if newpoint(1)>0 && newpoint(1)<=height && newpoint(2)>0 && newpoint(2)<width && flag(newpoint(1),newpoint(2))==0
                waiting(end+1,:)=newpoint;
                flag(newpoint(1),newpoint(2))=2;
            end
        end        
    end
end
figure,imshow(region),title('        ');
imwrite(region,'regiongrow.jpg');
    

python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像
image = cv2.imread('lotus1.jpg')
height, width, channel = image.shape
if channel == 3:
    image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

plt.imshow(image, cmap='gray')
plt.show()

# [seedx, seedy, button] = ginput(1) 在这里用鼠标点击代替，获取种子点的位置
seedx, seedy = np.round(plt.ginput(1)[0])
seedx, seedy = int(seedx), int(seedy)
region = np.zeros((height, width))
region[seedy, seedx] = 1
region_mean = image[seedy, seedx]
region_num = 1
flag = np.zeros((height, width))
flag[seedy, seedx] = 1
neighbor = np.array([[-1, -1], [-1, 0], [-1, 1], [0, -1], [0, 1], [1, -1], [1, 0], [1, 1]])

waiting = []
for k in range(8):
    y = seedy + neighbor[k, 0]
    x = seedx + neighbor[k, 1]
    waiting.append([y, x])
    flag[y, x] = 2

pos = 0
while pos < len(waiting):
    current = waiting[pos]
    pos += 1
    pixel = image[current[0], current[1]]
    pdist = abs(pixel - region_mean)
    if pdist < 40 / 255:
        region[current[0], current[1]] = 1
        region_mean = region_mean * region_num + pixel
        region_num += 1
        region_mean /= region_num
        for k in range(8):
            newpoint = current + neighbor[k]
            if 0 < newpoint[0] <= height and 0 < newpoint[1] < width and flag[newpoint[0], newpoint[1]] == 0:
                waiting.append(newpoint)
                flag[newpoint[0], newpoint[1]] = 2

plt.imshow(region, cmap='gray')
plt.title('')
plt.show()

cv2.imwrite('regiongrow.jpg', region * 255)

（2）区域合并

A：原理

区域合并：是一种图像分割技术，它的主要目标是通过合并相邻的像素或区域来生成更大的、具有相似特征的图像区域。与区域生长不同，区域合并是一种自底向上的方法，从单个像素或小区域开始，逐步将相邻的区域合并，直到满足某些预定义的合并条件。算法步骤如下

• 初始化： 将每个像素或小区域视为一个独立的区域。
• 相似性度量： 定义一种度量标准来衡量两个区域的相似性，这可以包括像素值、颜色、纹理、形状等特征。较低的相似性值意味着区域更相似。
• 合并条件： 设定一个合并条件，根据相似性度量来判断是否应该将两个相邻的区域合并。这可以是一个阈值，表示只有相似性高于阈值的区域才能合并。
• 区域合并： 从小区域开始，遍历图像的每个像素或区域，检查与相邻区域的相似性。如果两个相邻区域的相似性高于合并条件，则将它们合并成一个更大的区域。
• 迭代： 可能需要多次迭代才能达到最终的合并状态，因为合并一个区域可能会影响其他区域的合并条件

区域合并的优点在于它可以处理噪声和边界模糊的情况，同时能够生成比较平滑的分割结果。然而，合并条件的选择以及算法的实现都会影响最终的分割效果。此外，区域合并方法可能会忽略一些细节和纹理信息，因此在某些情况下可能无法获取到精细的分割结果。区域合并在实际应用中常用于医学图像分析、自然场景分析、遥感图像解译等领域，特别是在需要生成较大块的区域分割时，它可以是一个有用的工具

B：示例

C：程序

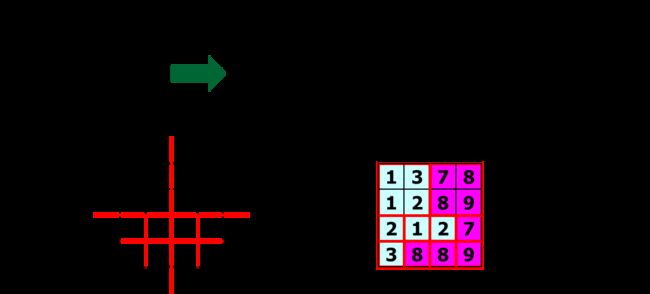
通过区域合并将示例中的小图像分割为两个区域

• 初始化：每个像素为一个小区域；相似性准则采用：相邻区域灰度均值差≤2；左上角第一个点设为区域1，其余为0，表示未标记
• 第一次扫描图像：从左到右，从上到下，判断每一点与其左上、上、左邻点的灰度距离，三个距离中最小的若符合合并规则，将对应邻点的标记赋予当前点；若没有相似的点，则赋予当前点新的标记
• 再次扫描图像：若某一像素点上、左邻点标记不一致，但当前点和其中一个邻点标记一致，则判断两个区域是否是同一个，若是，则将两个区域标记修改为较小的一个，即区域合并

---

matlab实现：

clear,clc,close all;

Image=[1 0 4 6 5 1;1 0 4 6 6 2;0 1 5 5 5 1;0 0 5 6 5 0;0 0 1 6 0 1;1 0 1 2 1 1];
[height,width,channel]=size(Image);
flag=zeros(height,width);
thresh=2;
neighbor=[-1 -1;-1 0;0 -1];
flag(1,1)=1;
number=1;
for j=1:height
    for i=1:width       
        pdist=[300 300 300];
        for k=1:3
            y=j+neighbor(k,1);
            x=i+neighbor(k,2);
            if x>=1 && y>=1
                pdist(k)=abs(Image(j,i)-Image(y,x));
            end
        end
        [mindist,pos]=min(pdist(:));
        if mindist<=thresh
            y=j+neighbor(pos,1);
            x=i+neighbor(pos,2);
            if flag(y,x)
                flag(j,i)=flag(y,x);
            end
        elseif mindist~=300
            number=number+1;
            flag(j,i)=number;            
        end
    end
end

for j=2:height
    for i=2:width  
        if flag(j-1,i)~=flag(j,i-1) && (flag(j,i)==flag(j-1,i) || flag(j,i)==flag(j,i-1))
            pdist=abs(Image(j-1,i)-Image(j,i-1));            
            if pdist<=thresh
                minv=min(flag(j-1,i),flag(j,i-1));
                maxv=max(flag(j-1,i),flag(j,i-1));
                flag(flag==maxv)=minv; 
            end
        end
    end
end       

python实现：

import numpy as np
import matplotlib.pyplot as plt

Image = np.array([[1, 0, 4, 6, 5, 1],
                  [1, 0, 4, 6, 6, 2],
                  [0, 1, 5, 5, 5, 1],
                  [0, 0, 5, 6, 5, 0],
                  [0, 0, 1, 6, 0, 1],
                  [1, 0, 1, 2, 1, 1]])

height, width = Image.shape
flag = np.zeros((height, width))
thresh = 2
neighbor = np.array([[-1, -1], [-1, 0], [0, -1]])
flag[0, 0] = 1
number = 1

for j in range(height):
    for i in range(width):
        pdist = [300, 300, 300]
        for k in range(3):
            y = j + neighbor[k, 0]
            x = i + neighbor[k, 1]
            if x >= 0 and y >= 0:
                pdist[k] = abs(Image[j, i] - Image[y, x])
        mindist, pos = min((val, idx) for (idx, val) in enumerate(pdist))
        if mindist <= thresh:
            y = j + neighbor[pos, 0]
            x = i + neighbor[pos, 1]
            if flag[y, x]:
                flag[j, i] = flag[y, x]
        elif mindist != 300:
            number += 1
            flag[j, i] = number

for j in range(1, height):
    for i in range(1, width):
        if flag[j - 1, i] != flag[j, i - 1] and (flag[j, i] == flag[j - 1, i] or flag[j, i] == flag[j, i - 1]):
            pdist = abs(Image[j - 1, i] - Image[j, i - 1])
            if pdist <= thresh:
                minv = min(flag[j - 1, i], flag[j, i - 1])
                maxv = max(flag[j - 1, i], flag[j, i - 1])
                flag[flag == maxv] = minv

plt.imshow(flag, cmap='tab20')
plt.title('')
plt.show()

（3）区域分裂

A：原理

区域分裂：是一种图像分割技术，与区域合并相反，它是从一个整体的区域开始，逐步将该区域分割成更小的子区域，直到满足某些预定的分割条件。区域分裂技术通常采用自顶向下的方法，从一个整体开始，逐步分解为子区域，直到每个子区域都满足特定的条件。算法步骤如下

• 初始化： 将整幅图像或整个区域视为一个初始区域。
• 划分条件： 设定一个划分条件，根据某些特定的准则来判断是否应该将一个区域继续分割为子区域。这可能涉及到像素值、颜色、纹理、形状等特征。
• 区域分裂： 从初始区域开始，检查该区域是否满足划分条件。如果满足条件，则将该区域分割成更小的子区域。
• 递归： 对于每个子区域，如果满足继续划分的条件，继续对子区域进行递归分割，直到不再满足划分条件为止。
• 重复： 反复执行区域分裂和递归步骤，直到所有满足条件的区域都被分割为止

区域分裂的优点在于它可以从整体开始，逐步地分解成具有相似特征的子区域，从而获得更准确的分割结果。然而，划分条件的选择以及算法的实现会影响最终的分割效果。另外，区域分裂算法可能在某些情况下产生过多的小区域，从而导致过度分割的问题。区域分裂在实际应用中通常用于医学图像分析、物体检测、图像分割等领域。在需要将图像分割为多个具有相似特征的区域时，区域分裂可以是一个有用的工具

B：示例

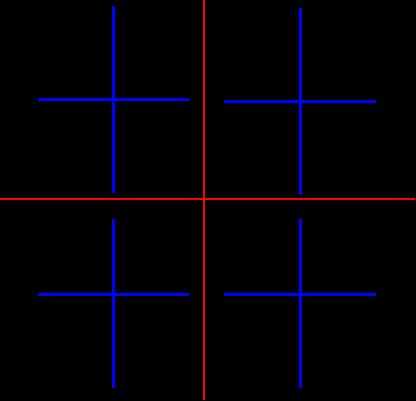
1：初始化及准则、方法的确定

• 区域内最大灰度值与最小灰度值之差$\le$ 2
• 采用一分为四的分裂方法

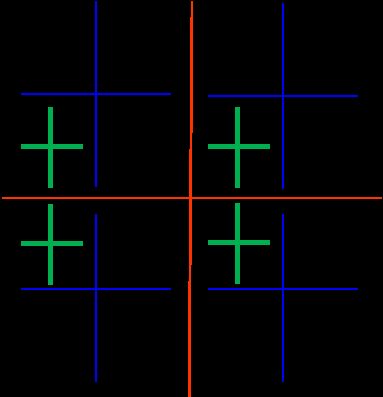
2：采用一分为四的分裂方法

对四个小区域分别计算最大与最小灰度差，与阈值2比较，每个区域均需分裂

依此类推，直至所有的区域都不能再分裂

C：程序

如下

---

matlab实现：

Image=imread('cameraman.jpg');          
S=qtdecomp(Image,0.27);                       
blocks=repmat(uint8(0),size(S));     
for dim=[256 128 64 32 16 8 4 2 1]
    numblocks=length(find(S==dim));
    if(numblocks>0)
        values=repmat(uint8(1),[dim dim numblocks]);
        values(2:dim,2:dim,:)=0;
        blocks=qtsetblk(blocks,S,dim,values);
    end
end

python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像
Image = cv2.imread('cameraman.jpg', cv2.IMREAD_GRAYSCALE)

# 进行 Quadtree 分解
S, _ = cv2.qr(Image, 0.27)

blocks = np.zeros_like(S, dtype=np.uint8)

for dim in [256, 128, 64, 32, 16, 8, 4, 2, 1]:
    numblocks = np.sum(S == dim)
    if numblocks > 0:
        values = np.ones((dim, dim, numblocks), dtype=np.uint8)
        values[1:dim, 1:dim, :] = 0
        blocks = cv2.qt_set_block(blocks, S, dim, values)

plt.imshow(blocks, cmap='gray')
plt.title('')
plt.show()

（4）区域分裂合并

A：原理

区域分裂合并：是一种图像分割方法，它结合了区域分割和区域合并的思想，旨在通过自底向上的方法将图像分割成具有相似特征的区域。该方法首先将图像划分成初始的小区域，然后根据一定的合并准则逐步合并相邻的区域，从而得到更大且更具一致性的区域。区域分裂合并方法的目标是在充分利用局部一致性的基础上，生成准确的分割结果。算法步骤如下

• 初始分割： 将整幅图像划分成初始的小区域，每个区域可以是单个像素或者更大的局部区域
• 分裂过程： 首先，对每个区域进行分裂判断，判断条件可以是像素之间的相似性、颜色一致性等。如果一个区域不满足分裂条件，那么该区域将不再继续分裂，否则将该区域继续分裂成更小的子区域
• 合并过程： 在分裂得到的小区域中，判断相邻的区域是否满足合并条件，合并条件可以是相似性高于阈值等。如果相邻区域满足合并条件，将它们合并成更大的区域
• 迭代： 反复执行分裂和合并过程，直到没有进一步的分裂和合并可以执行为止，生成最终的分割结果

区域分裂合并的优点在于它可以在自底向上的过程中处理不同尺寸的区域，从而在保留局部一致性的同时，获得更大范围的分割结果。然而，该方法的效率可能会受到区域分割和合并条件的选择以及算法实现的影响。区域分裂合并在实际应用中被广泛用于医学图像分析、遥感图像解译、自然场景分析等领域，特别适用于复杂场景下的图像分割任务

B：示例

二：基于聚类的图像分割

（1）原理

基于聚类的图像分割：把图像分割看做对像素进行分类的问题，把像素表示成特征空间的点，采用聚类算法把这些点划分为不同类别，对应原图则是实现对像素的分组，分组后利用“连通成分标记”找到连通区域。如何把像素表示成特征空间中的点
：用向量来代表像素或像素周围邻域，向量的元素为与像素相关的特征，根据图像的具体情况，判断待分割区域的共性来设计

（2）K均值聚类

• 略（请查看聚类专栏）

（3）程序

如下：

---

matlab实现：

clear,clc,close all;
Image=imread('fruit.jpg');
imshow(Image);
hsv=rgb2hsv(Image);
h=hsv(:,:,1);
h(h>330/360)=0;
[N,M]=size(h);
training=h(:);
startdata = [0;60/360;120/360;180/360;240/360;300/360];
[IDX,C]= kmeans(training,6,'Start',startdata);
idbw = (IDX == 1);
template = reshape(idbw, size(h));
figure,imshow(template),title('分割后的图像');
imwrite(template,'clusterseg.jpg');

python实现：

import cv2
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 读取图像
Image = cv2.imread('fruit.jpg')
Image = cv2.cvtColor(Image, cv2.COLOR_BGR2RGB)

# 显示原始图像
plt.imshow(Image)
plt.title('')
plt.show()

# 转换为HSV颜色空间并提取H通道
hsv = cv2.cvtColor(Image, cv2.COLOR_RGB2HSV)
h = hsv[:, :, 0]
h[h > 330] = 0  # 将大于330的值设为0

N, M = h.shape
training = h.reshape(-1, 1)
startdata = np.array([0, 60, 120, 180, 240, 300]) / 360

# 使用K均值聚类进行分割
kmeans = KMeans(n_clusters=6, init=startdata.reshape(-1, 1), n_init=1)
kmeans.fit(training)
labels = kmeans.labels_
centers = kmeans.cluster_centers_

idbw = (labels == 0)
template = idbw.reshape((N, M))

# 显示分割后的图像
plt.imshow(template, cmap='gray')
plt.title('')
plt.show()

cv2.imwrite('clusterseg.jpg', template * 255)