leetcode：134. 加油站

题目来源

• leetcode：gas-station

题目描述

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {

    }
};

题目解析

把这个题理解成下边的图就可以。

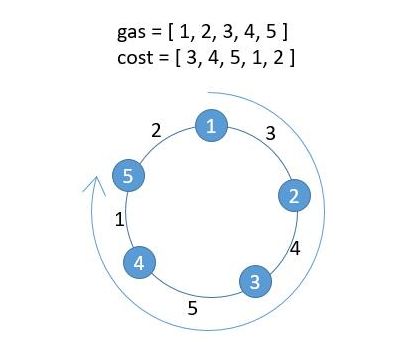
每个节点表示添加的油量，每条边表示消耗的油量。题目的意思就是问我们从哪个节点出发，还可以回到该节点。只能顺时针方向走。

暴力

遍历每一个加油站为起点的情况，模拟一圈。如果跑了一圈，中途没有断油，而且最后油量大于等于0，说明这个起点是ok的。

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        for (int i = 0; i < cost.size(); ++i) {
            int rest = gas[i] - cost[i];  // 记录剩余油量
            int index = (i + 1) % cost.size();
            while (rest > 0 && index != i){// 模拟以i为起点行驶一圈
                rest += gas[index] - cost[index];
                index = (index + 1) % cost.size();
            }
            // 如果以i为起点跑一圈，剩余油量>=0，返回该起始位置
            if(rest >= 0 && index == i){
                return i;
            }
        }
        return -1;
    }
};

class Solution {
public:
    int goodArray(vector<int>& gas, vector<int>& cost){
        int n = gas.size();
        //考虑从每一个点出发
        for (int i = 0; i < n; ++i) {
            int j = i;
            int remain = gas[i];
            while (remain - cost[i] >= 0){
                remain = remain - cost[j] + gas[(j + 1) % n];
                j = (j + 1) % n;
                if(j == i){
                    return i;
                }
            }
        }
        return false;
    }
};

for循环适合模拟从头到尾的遍历，而while循环适合模拟环形遍历，要善于使用while！

贪心

思路

这里gas和cost每一个位置都是对应的，并且实际意义上我们只需要知道二者的差值即可。

举个例子，在第i段路，给你2升汽油开车消耗1升汽油，是等价于给你100升汽油开车消耗99升汽油的。

这种情况，如果我们在把gas和cost看作两个数组会形成不必要的麻烦。

题目给了两种状态，首先是汽车起始汽油为0，然后行驶过程中汽车汽油必须足够行驶路程（也就是油表必须为正）。

我们假设油表可以为负值，这样如果存在题目中所说的唯一答案，那么当我们从0行驶到N后，油表为非负。如果油表为负值就返回-1；

那么我们怎么找从哪里开始出发呢？答案就是当我们油表值最小时，从这个点出发，我们的油表初始状态为0，之后也不会低于这个0，因为这个0其实就是油表最小值了。

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int n = gas.size();
        int cur_gas = 0, min_gas = 0, min_index = 0;//默认从0出发
        for (int i = 0; i < n; ++i) {
            cur_gas = cur_gas + gas[i] - cost[i];
            if(cur_gas < min_gas){
                min_gas = cur_gas;
                min_index = i + 1; 
            }
        }
        return cur_gas < 0 ? -1 : min_index;//油箱为负值返回-1；
    }
};

思路

有一个环形路上有n个站点； 每个站点都有一个好人或一个坏人； 好人会给你钱，坏人会收你一定的过路费，如果你带的钱不够付过路费，坏人会跳起来把你砍死； 问：从哪个站点出发，能绕一圈活着回到出发点?

• 首先考虑一种情况：如果全部好人给你 的钱加起来 小于 坏人收的过路费之和，那么总有一次你的钱不够付过路费，你的结局注定会被砍死。
• 假如你随机选一点 start 出发，那么你肯定会选一个有好人的站点开始，因为开始的时候你没有钱，遇到坏人只能被砍死；
• 现在你在start出发，走到了某个站点end，被end站点的坏人砍死了，说明你在 [start, end] 存的钱不够付 end点坏人的过路费，因为start站点是个好人，所以在 [start, end] 里任何一点出发，你存的钱会比现在还少，还是会被end站点的坏人砍死；
• 于是你重新读档，聪明的选择从 end+1点出发，继续你悲壮的征程； 终于有一天，你发现自己走到了尽头（下标是n-1)的站点而没有被砍死； 此时你犹豫了一下，那我继续往前走，身上的钱够不够你继续走到出发点Start?
• 当然可以，因为开始已经判断过（第一种情况中已经判断过了），好人给你的钱数是大于等于坏人要的过路费的，你现在攒的钱完全可以应付 [0, start] 这一段坏人向你收的过路费。 这时候你的嘴角微微上扬，眼眶微微湿润，因为你已经知道这个世界的终极奥秘：Start就是这个问题的答案。

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int n = gas.size();
        int total = 0;
        for (int i = 0; i < n; ++i) {
            total += (gas[i] - cost[i]);
        }
        if(total < 0){
            return -1;
        }
        
        int start = 0;
        int run_cost = 0;
        for (int i = 0; i < n; ++i) {
            run_cost += gas[i] - cost[i];
            if(run_cost < 0){
                start = i + 1;
                run_cost = 0;
            }
        }
        return start;
    }
};

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int curSum = 0;
        int totalSum = 0;
        int start = 0;
        for (int i = 0; i < gas.size(); i++) {
            curSum += gas[i] - cost[i];
            totalSum += gas[i] - cost[i];
            if (curSum < 0) {   // 当前累加rest[i]和 curSum一旦小于0
                start = i + 1;  // 起始位置更新为i+1
                curSum = 0;     // curSum从0开始
            }
        }
        if (totalSum < 0) return -1; // 说明怎么走都不可能跑一圈了
        return start;
    }
};

滑动窗口（重要）

加油站，怎么能往下继续走呢？？？就是我加的油量-取下一站的消耗量>=0，就能继续走

• 先直接把剩余油量数组弄出来offset=gas-cost
• 只要从一个i=0点出发，offset的累加剩余油>=0就行，从i=0–N-1都能搞定的话，N-1那会就意味着已经走到了出发点i=0
• 为了方便走成一个圈, 我们将累加剩余油叠加2次offset，得到sum, 比如：

            int[] gas = {1,2,3,4,5};
            int[] cost = {3,4,5,1,2};
            剩余油差：
            offset = [-2, -2, -2, 3, 3]
            剩余油差的累加和：
            sum = [-2, -4, -6, -3, 0, -2, -4, -6, -3, 0]

class Solution {
    int goodArray(vector<int>& gas, vector<int>& cost){
        int N = gas.size();
        int M = N << 1;

 
 	    //  为了方便走成一个圈, 我们将累加剩余油叠加2次offset，得到sum
        std::vector<int> offset(N);
        for (int i = 0; i < N; ++i) {
            offset[i] = gas[i] - cost[i];
        }

        std::vector<int> sum(M);
        //第一圈 
        int idx = 0;
        sum[idx++] = offset[0];
        for (int i = 1; i < N; ++i) {
            sum[idx] = sum[idx - 1] + offset[i];
            idx++;
        }
        //第2圈
        sum[idx] = sum[idx - 1] + offset[0];
        idx++;
        for (int i = 1; i < N; i++) {
            sum[idx] = sum[idx - 1] + offset[i];//累加
            idx++;
        }

        //得到了双拼的累加油差数组sum之后，开始从i==0--N-1判断，以N长度为窗口，找瓶颈最小值
        //这个瓶颈，就是在走一圈累加过程中最瓶颈的地方，如果它>=0，没问题
        //注意，首次i==0出发时，累加和瓶颈就是自己
        //但是i==1开始，注意累加和已经算上了i==0的点，需要把i-1之前的油量减掉
        std::deque<int> deque;
        for (int i = 0; i < 2 * N; ++i) {
            //每次一个N代表能走一圈
            //一个双端队列，左边放小的数，一旦i比尾部小，直接弹出尾部，保证左边头小
            while (!deque.empty() && sum[deque.back()] >= sum[i]){
                deque.pop_back();
            }
            deque.push_back(i);

            //窗口到N就过期，同时收集答案
            if(deque.front() == i - N){
                deque.pop_front();
            }
            if (i >= N - 1){
                //形成了一个窗口
                if (i == N - 1){//当窗口左边为0时，说明第一个窗
                    if (sum[deque.front()] >= 0) 
                        return 0;
                }
                else {//不是第一个窗口，就看瓶颈了
                    int min = sum[deque.front()] - sum[i - N];//减掉前面累加油量的瓶颈
                    if (min >= 0) return i - N + 1;//返回的是那个窗口的第一个位置
                }
            }
        }
    
        return -1;
    }
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        return goodArray(gas, cost);
    }
};

类似题目

题目	思路
leetcode：134. 加油站，能够走一圈的起点 Gas Station	滑动窗口（只要窗口内有一个瓶颈>=0，说明能以它为起点走一圈）
leetcode：780. (sx, ty)能够通过转换到达终点(tx, ty) Reaching Points	逆向思维，辗转相除法
782. 变为棋盘 Transform to Chessboard