SPOJ 2939 Query on a tree V

题目链接：http://www.spoj.com/problems/QTREE5/

题意：给出一棵树，初始时节点全是黑色。边的长度为1。两种操作：（1）修改某个节点的颜色；（2）询问到节点u的最近的白色节点到u的距离。

思路：（1）求得树链，建立每条链的线段树，用multiset保存每个节点i经过轻边到其子树内最近的白点的距离。线段树的节点[L,R]保存距离L最近、距离R最近的白点的距离。

（2）修改操作：若节点u的颜色变为白色，则将0插入multiset[u]，否则将0删掉。然后开始从u向上更新每条树链；

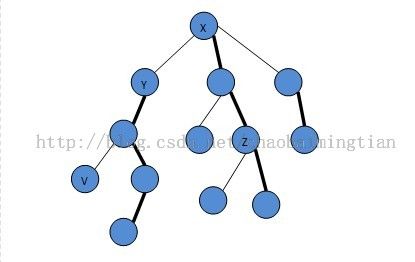
（3）询问操作：我们发现，对于询问v，设答案为z，那么v走到z节点必然是在某条树链的某个节点上转向了z。如下图，则依次从v向上在每条树链中查找即可。设此时到达x所在树链（注意x上方可能还有一些节点跟x在一个树链中，没有画出。另外，下面的图中z与x在一连链上，也可能答案在z经过轻边的子树中，总而言之都归结到z，我们使用multiset[z]就能找到那个），那么答案z可能在x上方，也可能在x下方，我们怎么知道在哪呢？我们只要在这条树链中以x为左侧查找一次、以x为右侧查找一次比较最优值即可。

struct node
{
    int L,R;
};


#define min3(a,b,c) min(min(a,b),c)
#define insert(x,y) x.insert(min(INF,y))
int father[N],pos[N],h[N];
multiset<int> f[N];
multiset<int>::iterator it;


void erase(multiset<int> &a,int x)
{
    it=a.find(x);
    if(it!=a.end()) a.erase(it);
}


struct chain
{
    vector<int> V;
    node *a;
    int n;


    void init()
    {
        n=SZ(V);
        int i;
        FOR0(i,SZ(V)) pos[V[i]]=i;
        a=new node[n<<2];
    }


    void pushUp(int t,int L,int R)
    {
        int m=(L+R)>>1;
        a[t].L=min3(INF,a[t*2].L,m-L+1+a[t*2+1].L);
        a[t].R=min3(INF,a[t*2+1].R,R-m+a[t*2].R);
    }


    void build(int t,int L,int R)
    {
        if(L==R)
        {
            it=f[V[L]].begin();
            a[t].L=a[t].R=*it;
            return;
        }
        int mid=(L+R)>>1;
        build(t*2,L,mid);
        build(t*2+1,mid+1,R);
        pushUp(t,L,R);
    }


    void modify(int t,int L,int R,int pos)
    {
        if(L==R)
        {
            it=f[V[pos]].begin();
            a[t].L=a[t].R=*it;
            return;
        }
        int mid=(L+R)>>1;
        if(pos<=mid) modify(t*2,L,mid,pos);
        else modify(t*2+1,mid+1,R,pos);
        pushUp(t,L,R);
    }


    int update(int x)
    {
        int u=V.back(),p=father[u];
        if(p) erase(f[p],a[1].R+1);
        modify(1,0,n-1,pos[x]);
        if(p) insert(f[p],a[1].R+1);
        return p;
    }


    int queryL(int t,int L,int R,int l,int r)
    {
        if(L==l&&R==r) return a[t].L;
        int mid=(L+R)>>1;
        if(r<=mid) return queryL(t*2,L,mid,l,r);
        if(l>mid) return queryL(t*2+1,mid+1,R,l,r);
        int opL=queryL(t*2,L,mid,l,mid);
        int opR=queryL(t*2+1,mid+1,R,mid+1,r);
        return min(opL,opR+mid-l+1);
    }




    int queryR(int t,int L,int R,int l,int r)
    {
        if(L==l&&R==r) return a[t].R;
        int mid=(L+R)>>1;
        if(r<=mid) return queryR(t*2,L,mid,l,r);
        if(l>mid) return queryR(t*2+1,mid+1,R,l,r);
        int opL=queryR(t*2,L,mid,l,mid);
        int opR=queryR(t*2+1,mid+1,R,mid+1,r);
        return min(opL+r-mid,opR);
    }


    int query(int u)
    {
        u=pos[u];
        int ans=INF,temp;
        temp=queryL(1,0,n-1,u,n-1); ans=min(ans,temp);
        temp=queryR(1,0,n-1,0,u); ans=min(ans,temp);
        return ans;
    }
};




chain c[N];
int belong[N];
vector<int> g[N];
int Q[N],size[N];
int n,m;


void DFS(int u)
{
    chain &ch=c[belong[u]];
    ch.init();
    int i,j,v;
    for(i=1;i<ch.n;i++)
    {
        u=ch.V[i];
        FOR0(j,SZ(g[u]))
        {
            v=g[u][j];
            if(v==father[u]||v==ch.V[i-1]) continue;
            DFS(v);
            insert(f[u],c[belong[v]].a[1].R+1);
        }
    }
    FOR0(i,ch.n)
    {
        insert(f[ch.V[i]],INF);
        insert(f[ch.V[i]],INF);
    }
    ch.build(1,0,ch.n-1);
}


int main()
{
    RD(n);
    int i,x,y,z;
    FOR1(i,n-1)
    {
        RD(x,y);
        g[x].pb(y);
        g[y].pb(x);
    }
    int head=0,tail=0;
    Q[++tail]=1;
    while(head<tail)
    {
        x=Q[++head];
        FOR0(i,SZ(g[x]))
        {
            y=g[x][i];
            if(y==father[x]) continue;
            Q[++tail]=y;
            father[y]=x;
        }
    }
    while(tail)
    {
        x=Q[tail--]; size[x]=1; z=0;
        FOR0(i,SZ(g[x]))
        {
            y=g[x][i];
            if(y==father[x]) continue;
            size[x]+=size[y];
            if(size[y]>size[z]) z=y;
        }
        if(z==0) belong[x]=x;
        else belong[x]=belong[z];
        c[belong[x]].V.pb(x);
    }
    FOR1(i,n) h[i]=1;
    DFS(1); RD(m);
    int op,ans,temp,t;
    while(m--)
    {
        RD(op,x);
        if(op==0)
        {
            if(h[x]) insert(f[x],0);
            else erase(f[x],0);
            h[x]^=1;
            while(x) x=c[belong[x]].update(x);
        }
        else
        {
            ans=INF; t=0;
            while(x)
            {
                temp=c[belong[x]].query(x);
                ans=min(ans,temp+t);
                t+=c[belong[x]].n-pos[x];
                x=c[belong[x]].V.back();
                x=father[x];
            }
            if(ans==INF) ans=-1;
            PR(ans);
        }
    }
}