数据结构之树:后序遍历二叉树(C & Python)
1 后序遍历
二叉树后序遍历的实现思想是:
从根节点出发,依次遍历各节点的左右子树,直到当前节点左右子树遍历完成后,才访问该节点元素
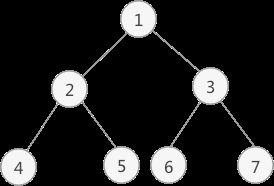
以上图 为例,采用后序遍历的思想遍历该二叉树的过程为:
- 从根节点 1 开始,遍历该节点的左子树(以节点 2 为根节点)
- 遍历节点 2 的左子树(以节点 4 为根节点)
- 由于节点 4 既没有左子树,也没有右子树,此时访问该节点中的元素 4,并回退到节点 2 ,遍历节点 2 的右子树(以 5 为根节点)
- 由于节点 5 无左右子树,因此可以访问节点 5 ,并且此时节点 2 的左右子树也遍历完成,因此也可以访问节点 2
- 此时回退到节点 1 ,开始遍历节点 1 的右子树(以节点 3 为根节点)
- 遍历节点 3 的左子树(以节点 6 为根节点)
- 由于节点 6 无左右子树,因此访问节点 6,并回退到节点 3,开始遍历节点 3 的右子树(以节点 7 为根节点)
- 由于节点 7 无左右子树,因此访问节点 7,并且节点 3 的左右子树也遍历完成,可以访问节点 3;节点 1 的左右子树也遍历完成,可以访问节点 1;
- 到此,整棵树的遍历结束
因此,上图中二叉树采用先序遍历得到的序列为:4 5 2 6 7 3 1
2 算法设计
- 根结点入栈
- 栈空则遍历结束,若非空则将栈顶结点设为当前结点,找到结点的左孩子,左孩子为空则进入操作4,左孩子不为空则将其入栈
- 重复操作2
- 结点右孩子不为空则将右孩子入栈,并修改该结点的右孩子为空;结点右孩子为空则代表结点的左右子树已遍历,访问该结点并将其出栈
- 重复操作2
3 C语言实现
代码:
'''C
#include
#include
#include
#define STACK_INITSIZE 100
#define STACK_INCREMENT 10
//******************************************************************
// 创建树
//******************************************************************
//树结点结构体
typedef struct node
{
int data;
struct node *lchild, *rchild;
}BiNode, *BiTree;
//创建一个简单的树,返回树的根结点指针
BiTree createBiTree()
{
BiTree T=(BiNode *)malloc(sizeof(BiNode));
T->data=1;
T->lchild=(BiNode *)malloc(sizeof(BiNode));
T->rchild=(BiNode *)malloc(sizeof(BiNode));
T->lchild->data=2;
T->lchild->lchild=(BiNode *)malloc(sizeof(BiNode));
T->lchild->rchild=(BiNode *)malloc(sizeof(BiNode));
T->lchild->rchild->data=5;
T->lchild->rchild->lchild=NULL;
T->lchild->rchild->rchild=NULL;
T->rchild->data=3;
T->rchild->lchild=(BiNode *)malloc(sizeof(BiNode));
T->rchild->lchild->data=6;
T->rchild->lchild->lchild=NULL;
T->rchild->lchild->rchild=NULL;
T->rchild->rchild=(BiNode *)malloc(sizeof(BiNode));
T->rchild->rchild->data=7;
T->rchild->rchild->lchild=NULL;
T->rchild->rchild->rchild=NULL;
T->lchild->lchild->data=4;
T->lchild->lchild->lchild=NULL;
T->lchild->lchild->rchild=NULL;
return T;
}
//****************************************************************
// 创建栈
//****************************************************************
//栈结构体
typedef struct
{
BiNode *base;
BiNode *top;
int size;
}BiStack;
//栈初始化
BiStack stackInit()
{
BiStack s;
s.base = (BiNode *)malloc(sizeof(BiNode)*STACK_INITSIZE);
s.top = s.base;
s.size =STACK_INITSIZE;
return s;
}
//入栈
void push(BiStack *s, BiNode e)
{
if(s->top - s->base >= s->size)
{
s->size += STACK_INCREMENT;
s->base = (BiNode *)realloc(s->base, sizeof(BiNode)*s->size);
}
*s->top = e;
s->top++;
}
//出栈
BiNode pop(BiStack *s)
{
BiNode temp;
s->top--;
temp = *s->top;
return temp;
}
//得到栈顶元素,但不出栈
BiNode getTop(BiStack s)
{
BiNode temp;
s.top--;
temp = *s.top;
return temp;
}
//*********************************************************************
// 使用栈结构后序遍历二叉树
//*********************************************************************
int time = 0; //记录访问结点次数
//访问结点
void visitNode(BiNode *root)
{
time++;
printf("第%d次访问的结点是:%d\n", time, root->data);
}
int cnt = 0; //记录栈变化次数
int stack[20][20]; //记录栈每次改变时栈中结点的数据
//遍历栈中结点
void traverseStack(BiStack s)
{
int i = 0;
while(s.base != s.top)
{
stack[cnt][i] = s.base->data;
i++;
s.base++;
}
stack[cnt][i] = 0XFFFFFFFF;
cnt++;
}
//后序遍历二叉树
void postTraverse(BiTree T)
{
BiStack bs = stackInit();
traverseStack(bs);
BiNode root = *T;
BiNode *temp = NULL;
push(&bs, root); //根结点入栈
traverseStack(bs);
while(bs.top != bs.base) //栈空表示遍历结束
{
root = getTop(bs);
temp = root.lchild; //先访问左孩子
while(temp != NULL) //左孩子不为空
{
//左孩子入栈
root = *temp;
temp = root.lchild;
push(&bs, root);
traverseStack(bs);
}
temp = root.rchild;
if(temp == NULL) //结点的右孩子为空,代表结点左右子树已遍历,可以访问该结点
{
visitNode(&root);
pop(&bs); //该结点已遍历,出栈
traverseStack(bs);
if(bs.top != bs.base) //栈非空时,栈顶结点左子树已遍历,修改其左孩子为空
{
root = pop(&bs);
root.lchild = NULL;
push(&bs, root);
}
}
else //结点的右孩子不为空,将右孩子入栈,并修改其右孩子为空
{
root = pop(&bs);
root.rchild = NULL;
push(&bs, root);
root = *temp;
push(&bs, root);
traverseStack(bs);
}
}
}
//************************************************************************************
// 主函数
//************************************************************************************
void main()
{
BiTree Tree = createBiTree();
printf("\n二叉树后序遍历结果如下\n");
postTraverse(Tree);
printf("\n\n栈中结点变化情况如下\n");
for(int i = 0; i < cnt; i++)
{
printf("栈中的结点有:");
int j = 0;
while(stack[i][j] != 0XFFFFFFFF)
{
printf("%d ", stack[i][j]);
j++;
}
printf("\n");
}
printf("\n\n");
system("date /T");
system("TIME /T");
system("pause");
exit(0);
} 运行结果:
4 Python实现
代码:
import datetime
import time
##################################################################################
# 二叉树
##################################################################################
#树结点类
class BiNode():
#创建结点,左右孩子为空
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None
#创建左右孩子结点
def creat(self, data1=0XFFFFFFFF, data2=0XFFFFFFFF):
if data1 != 0XFFFFFFFF:
self.lchild = BiNode(data1)
if data2 != 0XFFFFFFFF:
self.rchild = BiNode(data2)
#创建一棵简单的二叉树
def creatTree():
T = BiNode(1)
T.creat(2, 3)
T.lchild.creat(4, 5)
T.rchild.creat(6, 7)
return T
#############################################################################################
# 栈
#############################################################################################
#栈类
class Stack():
def __init__(self):
self.bs = []
def push(self, e):
self.bs.append(e)
def pop(self):
if self.bs:
return self.bs.pop()
else:
raise LookupError("stack is empty!")
def getTop(self):
return self.bs[-1]
####################################################################################
# 使用栈结构后序遍历二叉树
####################################################################################
time = 0 #记录访问结点次数
#访问结点的操作
def visitNode(node):
global time #将time设为全局变量
time += 1
print("第{}次访问的结点是:{}".format(time, node.data))
stackList = [] #记录栈中元素,列表的每个元素也为列表
#遍历栈,栈中结点的数据存储在stackList中
def traverseStack(treeStack):
global stackList
temp = []
for i in range(len(treeStack.bs)):
temp.append(treeStack.bs[i].data)
stackList.append(temp)
#后序遍历二叉树
def postTraverse(T):
treeStack = Stack()
traverseStack(treeStack)
treeStack.push(T)
traverseStack(treeStack)
while treeStack.bs != []: #栈空代表遍历结束
root = treeStack.getTop()
temp = root.lchild
while temp != None:
#左孩子入栈
treeStack.push(temp)
traverseStack(treeStack)
root = temp
temp = root.lchild
temp = root.rchild #后访问右孩子
if temp == None: #结点的右孩子为空,代表结点左右子树已遍历,可以访问该结点
visitNode(root)
treeStack.pop() #该结点已遍历,出栈
traverseStack(treeStack)
if treeStack.bs != []: #栈非空时,栈顶结点左子树已遍历,修改其左孩子为空
root = treeStack.getTop()
root.lchild = None
else:
treeStack.push(temp) #右孩子入栈
traverseStack(treeStack)
root.rchild = None #将结点右孩子设为空,代表已访问其右孩子
if __name__ == '__main__':
T = creatTree()
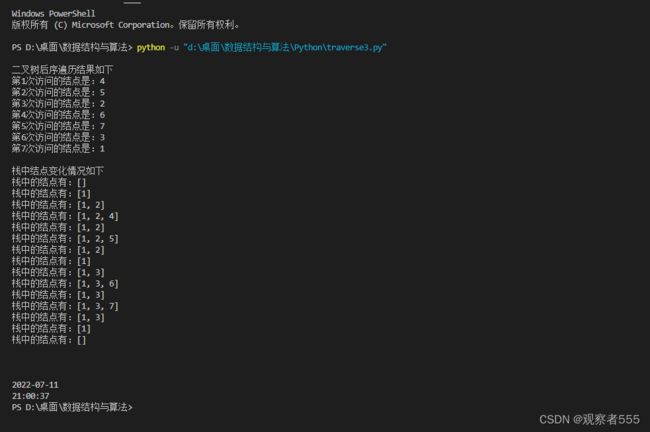
print("\n二叉树后序遍历结果如下")
postTraverse(T)
print("\n栈中结点变化情况如下")
for i in range(len(stackList)):
print("栈中的结点有:{}".format(stackList[i]))
print("\n\n")
datetime = datetime.datetime.now()
print(datetime.strftime("%Y-%m-%d\n%H:%M:%S")) 运行结果: