超详细 | 蚁群优化算法原理及其实现(Matlab)

蚁群优化算法ACO(Ant Colony Optimization Algorithm)是由意大利学者M.Dorigo等[1]于20世纪90年代初期受到自然界中真实蚂蚁觅食行为启发而提出的一种仿生优化算法。算法采用分布式并行计算机制，具有较强的鲁棒性，且易与其它优化算法相结合。取得了一系列较好的实验结果，其具有的诸多优良特性，使蚁群算法迅速受到研究者们的广泛关注[2]。

蚁群优化算法最早以求解离散问题优化为主，如旅行商问题(Traveling Sales-man Problem，TSP),并取得了较好的应用效果。随着算法的发展,学者们在基本蚁群算法基础上提出了诸多改进策略﹐有效提高了算法的求解性能﹐并逐渐将其扩展应用于诸如作业调度﹑路径规划﹑数据挖掘等多个领域,取得了丰富的研究成果[3]。

00 文章目录

1 蚁群优化算法原理
2 代码目录
3 算法性能
4 源码获取
5 总结

01 蚁群优化算法原理

蚁群算法 (ACO) 是一种启发式随机搜索算法, 它模拟了自然界中蚂蚁寻径过程。 基本原理：蚂蚁在觅食时, 最初是随机择路而行, 同时会分泌一种化学物质, 称为信息素, 残留于所行路径中, 之后, 随着迭代次数增加, 某条路径中信息素越来越多。 最终, 这些蚂蚁会选择某一条信息素最丰富的路走, 如此一来便找到了一条最优的路径。

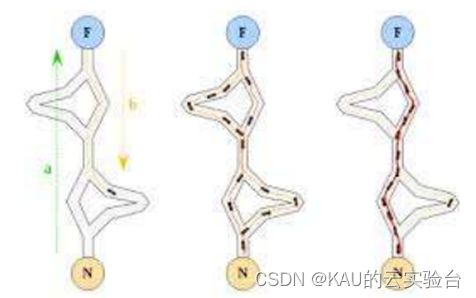
[D. Pal, P. Verma, D. Gautam and P. Indait, “Improved optimization technique using hybrid ACO-PSO,” 2016 2nd International Conference on Next Generation Computing Technologies (NGCT), Dehradun, India, 2016, pp. 277-282, doi: 10.1109/NGCT.2016.7877428. 在蚁巢和食物中找到最短路]
(1) 构建解空间
首先每只蚂蚁的起始位置都是任意的, 然后统计每只蚂蚁k下一个要访问的城市，直到全部蚂蚁访问完设置的全部城市. 在t时刻, 蚂蚁k从城市i转移到城市j的概率为pkij(t):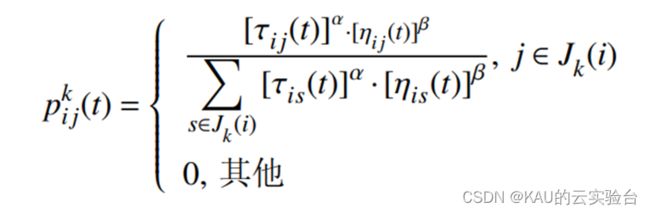

其中, α为信息素因子, β为启发函数因子;i,j分别为起始点和终点; nij(t)为两点之间长度的倒数;t为最大迭代次数; τij(t)为时间t由i到j的信息素含量;Jk(i)为所有没被访问过的节点的集合, 完全访问完成后表示一次循环结束.
(2) 更新信息素
记录在当前迭代次数上的最佳解 (最短路径), 并对不同城市的路线中的信息素含量做出了调整。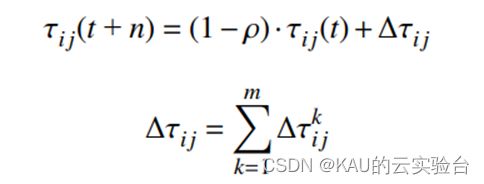

其中, ρ为信息素挥发因子, 取值范围一般在 [0.2, 0.5] 之间; 1-ρ为信息素残留系数; 第一个式子表示在访问过程结束后m只蚂蚁在城市i到j路径上留下的信息素总数. Δτkij为在本次循环中蚂蚁k在路径上留下的信息量, 由下式表示:
其中, Q为正常数, Lk为蚂蚁k在当前周期内蚂蚁通过路径长度。

(3) 判断是否结束
如果迭代次数少于最大迭代次数, 迭代次数加 1, 同时清空所有蚂蚁经过路线的记录表, 并返回步骤 1; 否则结束计算, 将得到的最优解进行输出处理.

02 代码目录

代码注释完整，其中部分程序如下：

代码获取方式见文末

03 算法性能

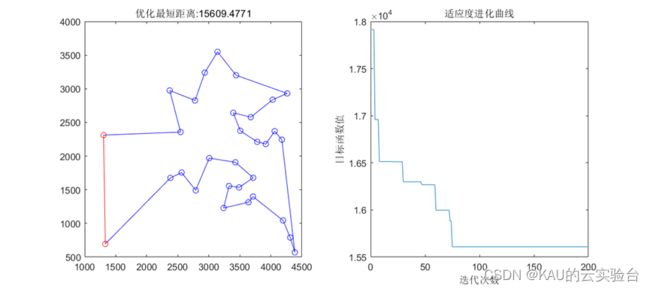
以典型的TSP问题来检验其性能，即找出遍历所有城市且距离最小的路径。
程序运行结果如下：

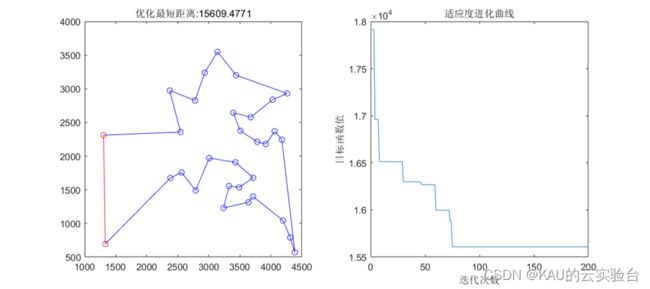
04 总结

本文介绍了蚁群算法应用于TSP问题，实际上蚁群算法虽然有很多优点，如：开放性、鲁棒性、分布式计算等优点‚但同时也存在搜索效率低、收敛速度慢、易陷入局部最优等缺点，因此存在继续改进该算法的空间。同时，蚁群算法不仅可应用于各种路径优化问题中，也可在连续问题中应用，后续作者也会更新这方面的文章，欢迎关注。

参考文献

[1] COLORNI A，DORIGO M，MANIEZZO V. Distributed optimiza-tion by ant colonies[C]. European Conference on Artificial Life，1991.
[2] 王永.多目标路由问题中的蚁群优化算法研究[D].长沙:湖南大学,2009.
• [3] 乔东平,裴杰,肖艳秋等.蚁群算法及其应用综述[J].软件导刊,2017,16(12):217-221.

蚁群算法MATLAB源码获取：
在作者公众号 KAU的云实验台 后台回复 ACO (大写字母)

另：如果有伙伴有待解决的优化问题（各种领域都可），可以发我，我会选择性的更新利用优化算法解决这些问题的文章。

如果这篇文章对你有帮助或启发，可以点击右下角的赞 (ง •̀_•́)ง(不点也行)