Matlab | 车辆路径规划应用实例（含源码）

在介绍了基本的TSP路径优化算法及简单示例后，针对现实中更加复杂的应用环境，其约束条件以及优化目标也将更加复杂，因此本文旨在更加复杂的VRP(Vehicle Routing Problem)数学模型下进行路径优化，帮助大家将模型与编程思想结合起来，希望能对各位有所帮助。

本文将以基于北斗的车辆路径问题动态规划研究为例进行论文的部分复现。

00 目录

车辆路径规划数学模型

混沌优化算法

算法流程

MATLAB程序实现

01 车辆路径规划数学模型

(来源于文献)

以用时最少建立车辆路径模型适度值函数：

02 混沌优化算法

 

03 算法流程

 

 04 MATLAB程序实现

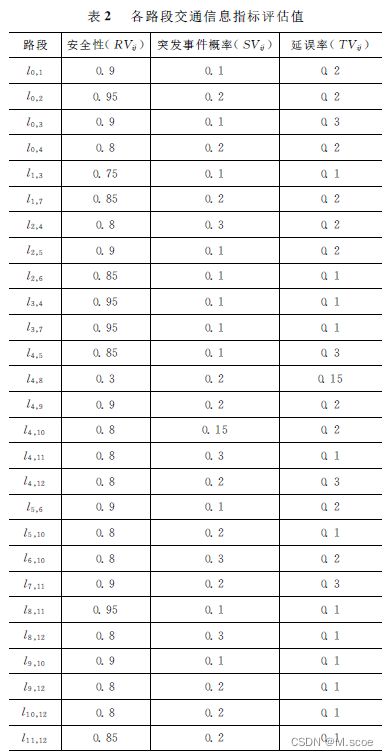
4.1 算例说明

 

 4.2 MATLAB程序实现

本文只对第一部分的问题进行求解，后面的规则修改其实也是在第一部分基础上稍作修改，因此以第一部分为主即可。

% <路径动态规划>
%---------------------------     Date      ---------------------------------
% 2022/5/10 - - > 2022
%---------------------------------------------------------------------------

clear all
clc

%% 参数

ST = xlsread('参数.xlsx','F2:G28');  %路径标号
X_Y = xlsread('参数.xlsx','A2:B14'); %坐标
N = size(X_Y,1);                       %路段个数
RV = xlsread('参数.xlsx','C2:C28');  %安全性
RV = transfer(RV,ST,N,1);
SV = xlsread('参数.xlsx','D2:D28');  %突发事件
SV = transfer(SV,ST,N);
TV = xlsread('参数.xlsx','E2:E28');  %延误
TV = transfer(TV,ST,N);
DS = Distanse(X_Y);                  %生成距离矩阵
X = zeros(N,N);                      %路径是否连通  0-12 连通赋1
for i=1:size(ST,1)
    X(ST(i,1)+1,ST(i,2)+1) = 1;
    X(ST(i,2)+1,ST(i,1)+1) = 1;
end
BL = double( RV==0 | SV==1 | TV==1); %受损路段
CT = [];                             %优化路径存储
m  = 1000;                           %最大搜索次数
T0 = 1;TD = 12;                      %出发与目标路段


%% 遗传参数

NIND   = 100;  %种群大小
MAXGEN = m;    %最大遗传代数
Pc     = 0.9;  %交叉概率
Pm     = 0.05; %变异概率
GGAP   = 0.9;  %代沟

%% 初始化种群

Chrom = InitPop(NIND,N,X,T0,TD);

%% 画出随机解的路径图

DrawPath(Chrom(1,:),X_Y);hold off
pause(0.0001)

%% 输出随机解的路径和总用时

disp('初始种群中的一个随机值:')
OutputPath(Chrom(1,:));
Rlength = Fitness(DS,RV,TV,SV,X,N,Chrom(1,:));
disp(['总距离：',num2str(Rlength)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')

%% GA优化

gen = 0;

for i=1:size(Chrom,1)
    ObjV(i) = Fitness(DS,RV,TV,SV,X,N,Chrom(i,:));  %计算路径长度
end
preObjV=min(ObjV);

while gen=0.5
        % 交叉操作
        SelCh = Recombin(SelCh,Pc,X,TD,T0,x);
    else
        % 变异
        SelCh = Mutate(SelCh,Pm,X,TD,T0,x);
        
    end
    
    %% 重插入子代的新种群
    
    Chrom = Reins(Chrom,SelCh,ObjV);
    
    %% 更新迭代次数
    
    gen=gen+1 ;
    
end
%% 画出最优解的路径图
for i=1:size(Chrom,1)
    ObjV(i) = Fitness(DS,RV,TV,SV,X,N,Chrom(i,:));  %计算路径长度
end

[minObjV,minInd]=min(ObjV);
DrawPath(Chrom(minInd(1),:),X_Y)

%% 输出最优解的路径和总距离

disp('最优解:')
p=OutputPath(Chrom(minInd(1),:));
disp(['总距离：',num2str(ObjV(minInd(1)))]);
disp('-------------------------------------------------------------')

其中，比较困难的是初始种群的产生规则，下面将贴出初始种群产生程序，并作了详细注释，本人能力有限，欢迎各位大佬一起讨论。

InitPop.m

%% 初始化种群
%输入：
% NIND：种群大小
% N：   个体染色体长度（这里为城市的个数）
%输出：
%初始种群
function Way = InitPop(NIND,N,X,T0,TD)

Way=zeros(NIND,N);%用于存储种群

for i=1:NIND

    flag = 1;% 判定标志 若flag==1则产生的路径不符合约束 flag==0符合约束
    while flag==1 
        Way(i,1)=T0; % 出发点
        p=2;  % p为下一个点

        newway = T0; %下一个路径的代号
        while newway~=TD % 如果下一个路径不是终点
            % 约束1 判断是否有路可走
            if wayjuge(newway,X,Way(i,:)) %判断这个路径后可选择的路径有哪些 如果有可选择的就随机选择一个
                %还有空余成员能选择
                newway = Randomway(newway,X,Way(i,:)); % 更新下一个路径
                Way(i,p) = newway; % 代入路径矩阵
                p = p+1; % 更新下一个点
            else
                %无路可走 重新来
                Way(i,:) = zeros(1,N); % 该点后面没有可选路径 重新赋0
                Way(i,1)=T0; %从初始点开始
                p=2; %同上
                newway = T0;%同上
            end
            
        end
        % 最终约束 包括不能包含重复节点 不少于最小节点数 最后一个点是终点
        % Way包含了不同路径，长度也不同
        flag = test(Way(i,:),TD); % 如果满足约束 赋值0 否则继续循环
    end
    
end

4.3 优化结果

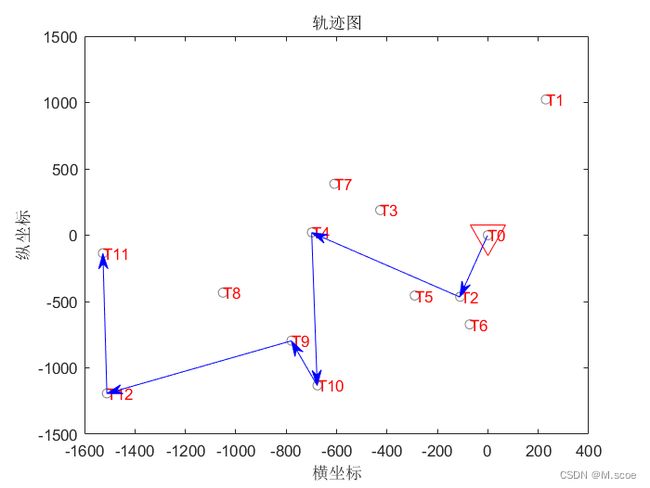
一个随机的路径如下：

经过算法优化后的路径如下，可以看到和原文中的初始路径结果保持一致。

以上就是本文的全部内容，任何问题欢迎大家积极讨论，代码地址：

链接：https://pan.baidu.com/s/1dZpO5B-WhnWKGAtxL0RKhQ?pwd=1111 
提取码：1111

欢迎关注作者微信公众号：川子凯 不定时分享有趣的代码或日常