旋转矩阵-rotation matrix简介

转载自：https://zhuanlan.zhihu.com/p/533911656，仅作学习记录

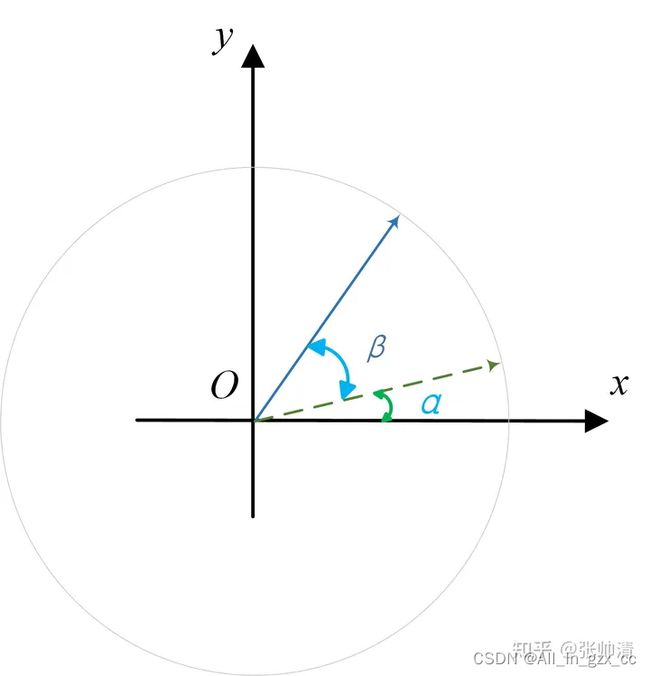
一、 二维旋转

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

#define canvas
fig, ax = plt.subplots()
line, = ax.plot([],[])

x0 = np.array([i for i in range(10)])
y0 = np.array([0 for i in range(10)])
#rotate
def rotate(x,y,theta):
    return x*np.cos(theta) + y *(-np.sin(theta)), x * np.sin(theta) + y * np.cos(theta)

def update(theta):
    ax.set_xlim(-10, 10)
    ax.set_ylim(-10, 10)
    ax.axis('equal')
    x,y = rotate(x0, y0, theta)
    line.set_data(x,y)
    return line

animation = FuncAnimation(fig, update, frames = np.linspace(0,np.pi*2, 200), interval = 50)

animation.save("rotate.gif", writer = "imagegick", fps = 10)
plt.show()

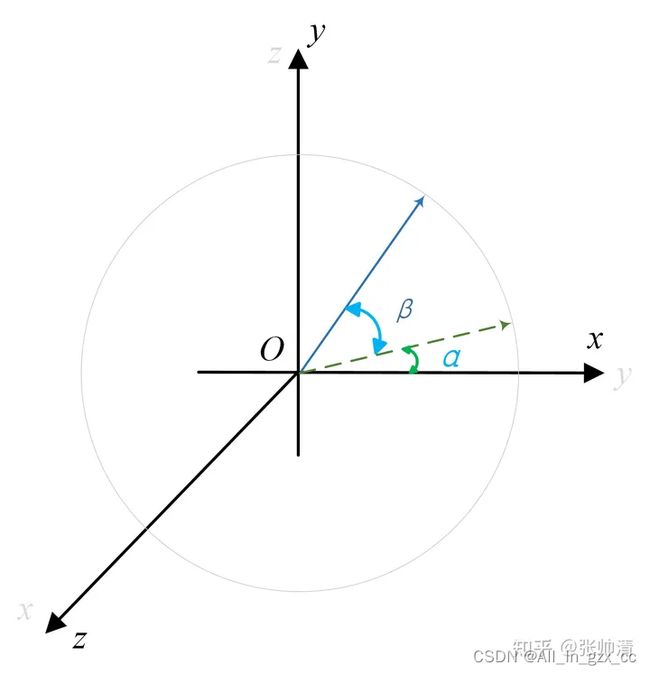
二、三维旋转

设距离旋转中心的距离为 ρ

1. 绕x轴旋转

2. 绕y轴旋转

3. 绕z轴旋转

三、例子

import numpy as np
import matplotlib.pyplot as plt

class Rotate(object):
    def __init__(self, dim = 2, x = 0, y = 0, alpha = 0, beta = 0, gamma = 0):
        self.dim = dim
        self.x = x
        self.y = y
        self.alpha = alpha
        self.beta = beta
        self.gamma = gamma
    def R2(self,alpha):
        return np.array([
            [np.cos(alpha), -np.sin(alpha)], 
            [np.sin(alpha), np.cos(alpha) ]
            ])
    def Rx(self, beta):
        return np.array([
            [1,            0,             0],
            [0, np.cos(beta), -np.sin(beta)],
            [0, np.sin(beta), np.cos(beta) ]
            ])
    def Ry(self, beta):
        return np.array([
            [np.cos(beta) , 0, np.sin(beta)],
            [0            , 1, 0           ],
            [-np.sin(beta), 0, np.cos(beta)]
            ])
    def Rz(self, beta):
        return np.array([
            [np.cos(beta), -np.sin(beta), 0],
            [np.sin(beta),  np.cos(beta), 0],
            [0           , 0            , 1]
            ])
    def R(self):
        pass

    def show(self):
        X = np.array([[1],[2]])
        
        Y = np.matmul(self.R2(np.pi/2), X)
        plt.scatter(X[0],X[1], color = "red")
        #plt.show()
        plt.scatter(Y[0],Y[1], color = "green")
        x1 = X[0,0]
        y1 = X[1,0]
        x2 = Y[0,0]
        y2 = Y[1,0]
        plt.plot([x1, 0], [y1, 0])
        plt.plot([x2, 0], [y2, 0])
        plt.axvline(x = 0, color = "blue", ls = "--", lw = 1)
        plt.axhline(y = 0, color = "blue", ls = "--", lw = 1)
        

        plt.axis("equal")
        plt.legend(["X","Y"])
        plt.show()
        
R = Rotate()
R.show()
'''
X = np.array([[1,0]]).T
print("X: ",X)
print("R: ",R.R2(np.pi/2))
print("ans: ", np.matmul(R.R2(np.pi/2), X))
'''

X = np.array([[1],[2]])
        Y = np.matmul(self.R2(np.pi/2), X)
        plt.scatter(X[0],X[1], color = "red")
        #plt.show()
        plt.scatter(Y[0],Y[1], color = "green")
        x1 = X[0,0]
        y1 = X[1,0]
        x2 = Y[0,0]
        y2 = Y[1,0]
        plt.plot([x1, 0], [y1, 0])
        plt.plot([x2, 0], [y2, 0])
        plt.axvline(x = 0, color = "blue", ls = "--", lw = 1)
        plt.axhline(y = 0, color = "blue", ls = "--", lw = 1)
        

        plt.axis("equal")
        plt.legend(["X","Y"])
        plt.show()