《SQUID: Deep Feature In-Painting for Unsupervised Anomaly Detection》论文阅读理解

《SQUID: Deep Feature In-Painting for Unsupervised Anomaly Detection》论文阅读理解

领域：用于医学图像的异常检测

论文地址：SQUID: Deep Feature In-Painting for Unsupervised Anomaly Detection

1 主要动机

对身体器官的射线扫描结果图片中展示了详细的结构化信息，充分利用这种身体各个部分之间的结构化信息，对检测出身体存在的异常非常重要；

2 主要贡献

1. 提出了使用空间感知队列来进行图片绘制和检测图片中存在的异常的方法（称为SQUID）；
2. 在两个胸部X射线基准数据集上，本文所提出的SQUID在无监督异常检测方面超过了13种最先进的方法至少5个百分点；
3. 本文还创建了一个新的数据集（DigitAnatomy），综合了胸部解剖的空间相关性和一致形状；

3 方法概述

3.1 训练过程

提出的模型可以根据递归解剖模式的空间位置对其进行分类，从而动态地维护视觉模式词典。文中指出，由于解剖学的一致性，健康图像中相同的身体区域有望表达相似的视觉模式，这使得异常模式的总数可以限定在一定范围内。

3.2 推理过程

训练过程得到的字典中不存在异常模式，因此，如果在推理时存在异常，那么所生成的射线图像是不符合常理的。

4 方法详述

流程详述
本文提出的方法大致可以总结为如下：

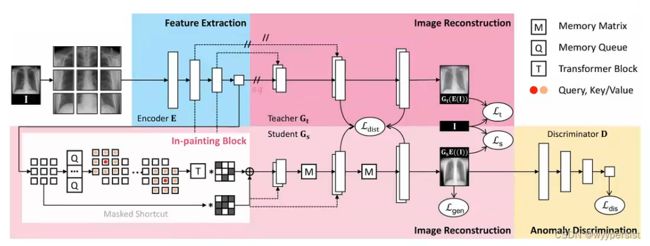
首先，将输入图像划分为$N\times N$个不重叠的块，并将它们输入编码器进行特征提取。

然后，训练两个生成器来重建原始的图像，重建的同时，创建一个解剖模式字典，并通过一个新的记忆队列动态更新；其中，教师生成器直接使用编码器提取的特征，而学生生成器则使用由绘制块增强的特征；教师生成器和学生生成器通过知识蒸馏的方式进行耦合。

最后，使用鉴别器来评估学生生成器重建得到的图像的真假。

上述过程经过训练之后可以用于检测图像中是否存在缺陷。

4.1 总述

4.1.1 特征提取

特征提取模块可以是任何骨干网络，文中使用了基本的卷积和池化层。

4.1.2 图像重建

文中引入教师T和学生S生成器来重建原始图像。在重建的过程中，解剖模式的字典将被创建并用于动态更新记忆队列。

具体来说，教师生成器使用编码器（使用了自动编码器[1]）提取的特征直接重建图像。另一方面，学生生成器使用了在绘制模块中增强的特征。教师和学生生成器通过知识提取范式[2]在所有上采样水平上耦合。学生生成器的目标是根据增强特征重建正常图像，然后将其用于异常判别器中；而教师生成器则是用作防止学生不断生成相同正常图像的正则化器。

4.1.3 异常判别

使用鉴别器来评估生成的图像是真的还是假的，值得注意的是，只有学生生成器进行梯度下降优化，教师生成器和学生生成器鉴别器同时竞争，直到两个生成器在训练过程中收敛。经过训练的鉴别器可用于检测测试图像中的异常。

4.2 将记忆队列用作词典

4.2.1 使用动机

记忆队列经常被用作异常检测任务，为了创造“正常”外观，通过对记忆队列中的相似模式进行加权平均来增强特征。但是这种增强忽略了图像中的空间信息而无法感知解剖图像的一致性。

4.2.2 空间感知记忆机制

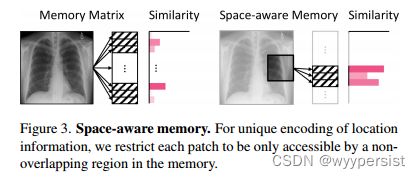
因此，为了解决上述存在的模型对空间感知能力不足的问题，将分割的小块patch传入到模型中，这些patch块与原始图像的唯一位置标识符相关联。

同时，文中指出，为了保证位置信息的唯一编码，将每个patch块限制为只能由内存矩阵中的非重叠区域访问。即特定位置的patch快只能访问记忆矩阵中的相应段。如图3所示。

4.2.3 内存队列

由于在记忆矩阵中“正常模式”的特征是通过组合矩阵中的学习基础而形成的。但是，这种组合形成的正常特征实际上和实际图像特征之间还存在一定的分布上的差异。

文中为了解决上述的问题，提出了一个内存队列来存储模型训练期间的真实图像特征，从而实现真实分布。在训练期间直接将之前输入的特征复制到队列结构中，经过训练之后，记忆队列用作正常解剖模式的字典。为了验证该说法的准确性，文中还提供了t-SNE可视化图，来验证记忆矩阵中的学习基础（蓝色点）和训练集的实际图像特征（灰色点）的分布不同。从图4中可以看出，内存队列中存储的红色特征点和实际图像特征具有相同的分布。

4.2.4 Gumbel shrinkage

文中指出，控制记忆存储中的激活模式的数量对异常检测是有利的。但是，单纯使用topk个存储中的模式进行激活时，存储中剩下的模式将无法进行梯度下降更新。为了实现所有存储中的模式梯度得到更新，文中提出了一个Gumbel收缩模式：
$$w^{\prime }=sg(hs(w,topk(w))-\varphi (w))+\varphi (w)$$
其中，$w$表示图像特征与存储中的条目之间的相似度，$sg(\cdot )$
表示停止梯度操作算子。$hs(\cdot ,t)$表示具有阈值t的硬收缩操作算子，$\varphi (\cdot )$表示Softmax函数。

如此，在前向传播中，Gumbel收缩确保了存储中前k个最相似的条目的组合；在反向传播过程中，Gumbel收缩起到Softmax的作用。在文中提出的框架中，将Gumbel收缩应用于内存队列和内存矩阵。

4.3 公式化基于图像修复的异常检测流程

4.3.1 动机

由于经典的图像恢复工作中会将待修复区域与周围存在的边界伪影相关联，这样恢复出来的图像会使得后期的异常检测不准确。为了解决该问题，文中提出了在图像的特征级别上进行恢复重建。

4.3.2 图像特征级恢复模块

文中将内存队列集成到一个新颖的图像修复块中，以执行图像修复中的特征空间。

该模块从记忆队列开始，该内存队列将$w\times h$非重叠patch特征$F_{(1,1),...,(w,h)}$补充为和他们最接近的“正常”特征$N_{(1,1),...,(w,h)}$。由于$N$是从先前训练数据中提取的特征组合而成的，因此$N$不受当前输入图像的影响。

为了聚合输入图像的特征，文中使用transformer块来聚合patch特征$F$和增强后的特征$N$。详细来说，对于每个patch块$F_{i,j}$，其空间上相邻的8个增强的$N_{(i-1,j-1),...,(i+1,j+1)}$被用作细化$F_{i,j}的条件$。

其中，transformer块中的query token为展平处理之后的$F_{(i,j)}\in R^{1\times \ast }$，同时，key/value tokens为$N_{(i-1,j-),...,(i+1,j+1)}\in R^{8\times \ast }$。

在上述图像修复模块中，文中还应用了一对额外的$1\times 1$卷积。

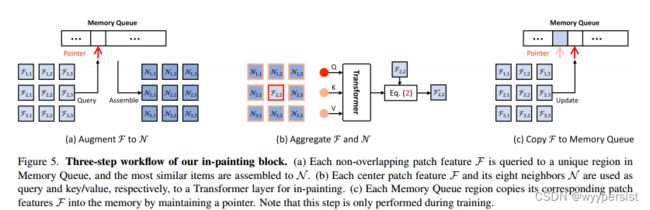
4.3.3 带有掩膜的shortcut快捷连接

文中还在图像恢复模块的开始，对输入的特征添加掩膜之后，直接连接到图像恢复模块中transformer块的输出上，共同作为后边学生重建模块的输入。

文中指出，随即使用二进制掩膜来门控shortcut特征。

总的来说，上述过程可以表示为如下公式：
$$F^{\prime }=(1-\sigma )\cdot F+\sigma \cdot inpant(F)$$
其中，$inpant(\cdot )$即为上述描述的图像恢复模块。$\sigma Bernoulli(\rho )$，其中$\rho$为门控概率。在每个训练步骤得到$F^{\prime }$之后，初始的$F$被复制以更新记忆队列，见图5c。

在推理时，完全禁用shortcut方式，$F^{\prime }=inpaint(F)$用于确定性的预测。

4.4 异常判别

由于训练的时候使用的只有正常样本特征，那么在推理测试的时候使用的带有异常特征的图像在重建之后，看起来不是很自然，那么这个时候就可以在重建后的图像上定位缺陷点。

文中提出的图像恢复模块专注于将任何patch块特征（正常或异常）增强为类似的“正常”特征。学生生成器根据这些“正常”特征重建“正常”图像，而教师生成器用于防止学生生成与输入无关的相同图像。

那么，经过训练之后，学生生成器得到的重建图像和原始的输入图像之间的语义差异会很小，如果原始输入为正常图像；相反地，如果原始输入为异常图像，那么，语义差异会很大。然后，使用鉴别器网络来感知原始输入和学生生成器重建之后的图像之间的差异，来获得异常点情况。

上述过程可以表示为如下公式形式，一个图像的异常分数$A$可以通过如下公式获得，其中，编码器、教师生成器、学生生成器和鉴别器分别标记为$E,G_t,G_s,D$。
$$A=\varphi (\frac{D(G_s(E(I)))-u}{\sigma })$$
其中，$\varphi (\cdot )$表示Sigmoid函数，$u$和$\sigma$分别表示在训练集上计算的异常分数的平均值和标准差。

4.5 损失函数

文中提出的模型使用5个loss函数来进行约束。重建图像与原始输入图像之间的均方误差（MSE）使用在教师生成器和学生生成器之间。
（$L_s$和$L_t$）

同时，使用$L_{dist}={\sum }_{i=1}^l(F_t^i-F_s^i{)}^2$作为教师生成器与学生生成器之间在图像$l$个特征层上的距离约束函数，其中$l$表示特征层总数。

此外，文中还是用了类似于DCGAN[3]中间的对抗损失函数去改进学生生成器生成的图像质量。具体来说，使用如下函数：
$$L_{gen}=log(1-D(G_s(E(I))))$$
鉴别器使得真实图像的平均概率和生成图像的反转概率最大化，使用如下公式：
$$L_{dis}=log(D(I))+log(1-D(G_s(E(I))))$$

总的来说，基于文中提出模型的5个损失函数，需要最小化生成损失$({\lambda }_t{L}_t+{\lambda }_s{L}_s+{\lambda }_{dist}{L}_{dist}+{\lambda }_{gen}{L}_{gen})$，同时最大化鉴别损失$({\lambda }_{dis}{L}_{dis})$。

5 实验

5.1 数据集

文中使用了自行创建数据集（DigitAnatomy）和公共数据集（ZhangLab Chest X-ray[4]、Stanford CheXpert[5]）

5.2 选择的Baselines和评价指标

文中使用13个主要基线与本文提出的模型进行直接比较：Auto-Encoder、VAE；Ganomaly，f-AnoGAN，IF，SALAD；以及MemAE、CutPaste、M-KD、PANDA、PaDiM、IGD。

文中使用标准指标评估性能：受试者工作特征（ROC）曲线、ROC曲线下面积（AUC）、准确度（Acc）和F1分数（F1）。

文中指出，对所有模型都在训练集上从头开始训练3次。

6 实验结果

图6展示了文中提出的SQUID模型与其他基线模型的实验结果对比。其中，使用文中所提出的图像恢复方法在自主创造的数据集上更具有鲁棒性。

表1展示了文中所提模型SQUID在公共数据集上与其他基线模型的实验结果对比。

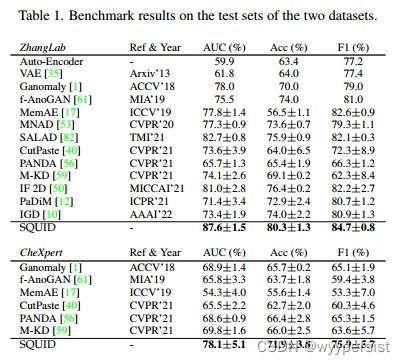
图7显示SQUID在两个公共数据集上的ROC曲线，表明文中提出的方法在灵敏度和特异性之间产生了最佳的权衡。

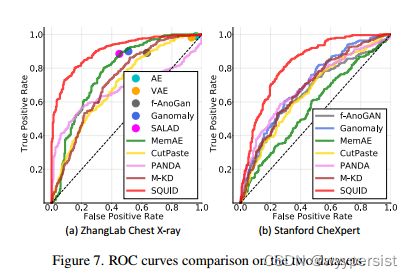
图8展示了文中所提模型在两个公共数据集上对正常样本和异常样本进行重建的结果。

文章局限性：无法精确定位像素级的异常。只能在图像层面提供分类的AUROC指标。

参考文献

[1] David E Rumelhart, Geoffrey E Hinton, and Ronald J Williams. Learning internal representations by error propagation. Technical report, California Univ San Diego La Jolla Inst for Cognitive Science, 1985. 3
[2] Geoffrey Hinton, Oriol Vinyals, and Jeff Dean. Distilling the knowledge in a neural network. arXiv preprint arXiv:1503.02531, 2015. 3
[3] Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434, 2015. 5
[4] Daniel S Kermany, Michael Goldbaum, Wenjia Cai, Carolina CS Valentim, Huiying Liang, Sally L Baxter, Alex McKeown, Ge Yang, Xiaokang Wu, Fangbing Yan, et al. Identifying medical diagnoses and treatable diseases by image-based deep learning. Cell, 172(5):1122–1131, 2018. 2, 6
[5] Jeremy Irvin, Pranav Rajpurkar, Michael Ko, Yifan Yu, Silviana Ciurea-Ilcus, Chris Chute, Henrik Marklund, Behzad Haghgoo, Robyn Ball, Katie Shpanskaya, et al. Chexpert: A large chest radiograph dataset with uncertainty labels and expert comparison. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 33, pages 590–597, 2019. 2, 6