数据结构基础：P9.4-排序(一)---＞归并排序

本系列文章为浙江大学陈越、何钦铭数据结构学习笔记，前面的系列文章链接如下：
数据结构基础：P1-基本概念
数据结构基础：P2.1-线性结构—＞线性表
数据结构基础：P2.2-线性结构—＞堆栈
数据结构基础：P2.3-线性结构—＞队列
数据结构基础：P2.4-线性结构—＞应用实例：多项式加法运算
数据结构基础：P2.5-线性结构—＞应用实例：多项式乘法与加法运算-C实现
数据结构基础：P3.1-树(一)—＞树与树的表示
数据结构基础：P3.2-树(一)—＞二叉树及存储结构
数据结构基础：P3.3-树(一)—＞二叉树的遍历
数据结构基础：P3.4-树(一)—＞小白专场：树的同构-C语言实现
数据结构基础：P4.1-树(二)—＞二叉搜索树
数据结构基础：P4.2-树(二)—＞二叉平衡树
数据结构基础：P4.3-树(二)—＞小白专场：是否同一棵二叉搜索树-C实现
数据结构基础：P4.4-树(二)—＞线性结构之习题选讲：逆转链表
数据结构基础：P5.1-树(三)—＞堆
数据结构基础：P5.2-树(三)—＞哈夫曼树与哈夫曼编码
数据结构基础：P5.3-树(三)—＞集合及运算
数据结构基础：P5.4-树(三)—＞入门专场：堆中的路径
数据结构基础：P5.5-树(三)—＞入门专场：File Transfer
数据结构基础：P6.1-图(一)—＞什么是图
数据结构基础：P6.2-图(一)—＞图的遍历
数据结构基础：P6.3-图(一)—＞应用实例：拯救007
数据结构基础：P6.4-图(一)—＞应用实例：六度空间
数据结构基础：P6.5-图(一)—＞小白专场：如何建立图-C语言实现
数据结构基础：P7.1-图(二)—＞树之习题选讲：Tree Traversals Again
数据结构基础：P7.2-图(二)—＞树之习题选讲：Complete Binary Search Tree
数据结构基础：P7.3-图(二)—＞树之习题选讲：Huffman Codes
数据结构基础：P7.4-图(二)—＞最短路径问题
数据结构基础：P7.5-图(二)—＞哈利·波特的考试
数据结构基础：P8.1-图(三)—＞最小生成树问题
数据结构基础：P8.2-图(三)—＞拓扑排序
数据结构基础：P8.3-图(三)—＞图之习题选讲-旅游规划
数据结构基础：P9.1-排序(一)—＞简单排序(冒泡、插入)
数据结构基础：P9.2-排序(一)—＞希尔排序
数据结构基础：P9.3-排序(一)—＞堆排序

---

一、有序子列的归并

要说到规定排序，它的一个核心就是两个有序子列的归并。我们来看个例子：

假设我们有两个子序列，这两个子序列本身已经是排好序的。我们的目标是开另外一个数组，然后要把这些数字一个一个的放到这个数组里面去，然后希望最后这个数组是从小到大有序的。

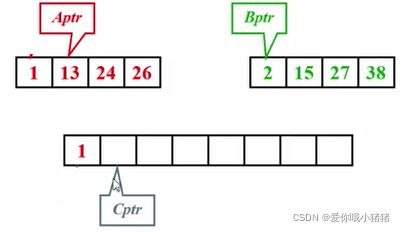
其实这个算法很简单，跟之前两个多项式相加的想法是非常相似的。我们先要准备好三个指针，A指针指向A序列当前第一个元素。B指针指向B序列当前第一个元素。C指针指向现在我要放的这个元素的位置。

第一次比较，1更小，放入新数组中，并将A指针和C指针向后移动1位。

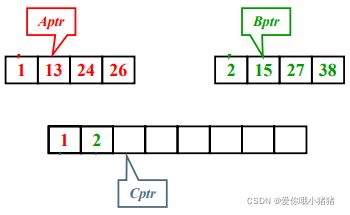
继续比较，2更小，放入新数组中，并将B指针和C指针向后移动1位。

接下来就一直重复就行了。。。

算法对应代码如下：

/* L = 左边起始位置, R = 右边起始位置, RightEnd = 右边终点位置 */
void Merge( ElementType A[], ElementType TmpA[], 
int L, int R, int RightEnd ) 
{ 
	LeftEnd = R - 1; /* 左边终点位置。假设左右两列挨着 */
	Tmp = L; /* 存放结果的数组的初始位置 */
	NumElements = RightEnd - L + 1; 
	while( L <= LeftEnd && R <= RightEnd ) {
		if ( A[L] <= A[R] ) TmpA[Tmp++] = A[L++]; 
		else TmpA[Tmp++] = A[R++]; 
	}
	while( L <= LeftEnd ) /* 直接复制左边剩下的 */ 
		TmpA[Tmp++] = A[L++]; 
	while( R <= RightEnd ) /*直接复制右边剩下的 */ 
		TmpA[Tmp++] = A[R++]; 
		//从后往前导
	for( i = 0; i < NumElements; i++, RightEnd -- ) 
		A[RightEnd] = TmpA[RightEnd]; 
}

二、递归算法

2.1 算法实现

归并算法在谈到具体实现的时候，其实有两种不一样的实现的策略，我们先从比较容易理解的递归算法开始看。

归并排序的递归算法就是一种非常典型的分而治之策略的应用。什么叫分而治之呢？我们其实之前也讨论过，就是假设我们待排的序列是放在一个数组里头，我把它一分为二，然后我递归的去把左边排好序，我再递归的去把右边排好序。这样我就得到了两个有序的子序列，而且他们肩并肩的放在一起，最后就调用上面写的归并算法把这两个有序的子序列归并成最终的有序序列。

对应代码如下：

void MSort( ElementType A[], ElementType TmpA[],
int L, int RightEnd ) 
{ 
	int Center; 
	if ( L < RightEnd ) {
		Center = ( L + RightEnd ) / 2;  //中间位置
		MSort( A, TmpA, L, Center ); //递归处理左边
		MSort( A, TmpA, Center+1, RightEnd );  //递归处理右边
		Merge( A, TmpA, L, Center+1, RightEnd ); //归并两个有序序列
	} 
}

算法复杂度：

假设我们解决整个问题用的时间是$T(N)$的话，那么我们递归的去解决左半边用的时间就一定是$T(N/2)$，因为数据的规模减了一半。递归的去解决右半边用的时间也是$T(N/2)$。然后我们还需要执行一步Merge规并，这一步的时间复杂度$O(N)$数量级。
$\mathrm{T}(\mathrm{N})=\mathrm{T}(\mathrm{N}/2)+\mathrm{T}(\mathrm{N}/2)+\mathrm{O}(\mathrm{N})\mathrm{T}(\mathrm{N})=\mathrm{O}(\mathrm{N}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{N})$
这个$\mathrm{N}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{N}$是非常强的$\mathrm{N}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{N}$，它没有最好时间复杂度，也没有最坏时间复杂度，也没有平均时间复杂度，任何情况下它都是$\mathrm{O}(\mathrm{N}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{N})$

2.2 接口定义

我们在最开始的时候有一个约定，我们在讨论任何排序算法的时候都要有一个统一的接口，传进来的参数只能是原始的数组A
加上这个数组里面元素的个数N。所以这个MSort的函数是不满足这个条件的，于是我们必须要给用户一个非常友好的统一的函数接口，对应代码如下：

void Merge_sort( ElementType A[], int N ) 
{ 
	ElementType *TmpA;
	TmpA = malloc( N * sizeof( ElementType ) ); 
	if ( TmpA != NULL ) { 
		MSort( A, TmpA, 0, N-1 ); 
		free( TmpA ); 
	} 
	else Error( “空间不足" ); 
}

在这段代码里可能会有一个令人疑惑的地方：为什么MSort要一直带着这个TmpA呢？整个程序的执行过程中，真正用到TmpA是在那个Merge函数里面，为什么我们不直接在Merge函数的内部去声明这个TmpA呢？

①如果我们在Merge_sort里面刚进去的时候就声明了另外一个等长的数组TmpA，然后我进入了MSort，把这个问题一分为二，就开始递归的去解决这个问题。在递归的过程中间，我们从始至终都是在同一个数组的某一段上面反反复复的做Merge操作。从头到尾我这个malloc只调用了一次，整个程序执行完了以后这个 free也只执行了一次。

②如果我只在Merge中间声明一个临时数组，在这个递归程序里面我要反复地去malloc反复地去free，这样做很不划算。

三、非递归算法

之所以我们先介绍一个递归的算法，是因为我们觉得递归算法可能比较容易理解。当然了数据结构学到现在，我相信你已经知道递归算法在真正实现的时候其实并不是那么美妙的，因为他要占用系统的堆栈，而且他有很多额外的操作都让他比较慢。

规并排序也可以用不递归的算法做出来，基本思路如下：

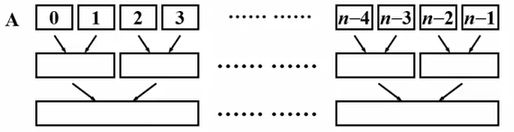
我假设在一开始的时候一共有n个有序的子序列，每一个子序列里都只含有一个元素

下一步我把相邻的两个有序的子序列做一次规并，于是我就形成了若干个有序的子序列，每个子序列的长度就变成了2

然后我继续规并两个相邻的子序列，又产生了一系列有序的子序列，这些子序列的长度就变成了4

以此类推，一直到最后我得到一个完整的有序的序列

算法分析：

①这个算法过程是非常容易理解的，但是这个算法需要额外的空间复杂度有点恐怖的。上图中的深度是$logN$，如果在每一层我要开一个新的临时数组去存这个中间结果的话，那么我的额外空间复杂度就变成$NlogN$。
②但是换一个角度讲，真的有必要这么做吗？我们要用这个非递归的算法去实现规并排序的话，能够做到最小的额外空间复杂度是$O(N)$。实际上我们只要开一个临时数组就够了，第一次我们把A规并到临时数组里面去。第二次就可以把临时数组里面的东西归并回A里面去，然后再把A归并到临时数组里头，然后再把临时数组导回到A。

一趟归并对应代码如下：

//一趟归并：
void Merge_pass( ElementType A[], ElementType TmpA[], int N,
int length ) /* length = 当前有序子列的长度 */
{ 
	//i左到N-2*length就行了，因为如果N是奇数，那么会剩一个元素归并不了，我们最后去处理这个尾巴
	for ( i=0; i <= N–2*length; i += 2*length )
	//这里我们使用Merge1这个名字，因为传统Merge把结果放到A里面，我们这里要把结果放到TmpA里面
		Merge1( A, TmpA, i, i+length, i+2*length–1 );
	if ( i+length < N ) /* 归并最后2个子列，处理尾巴 */
		Merge1( A, TmpA, i, i+length, N–1);
	else /* 最后只剩1个子列 */
		//说明归并完了，往A导入即可
		for ( j = i; j < N; j++ ) TmpA[j] = A[j];
}

下来我们再看我们的原始的统一的接口应该怎么写

void Merge_sort( ElementType A[], int N ) 
{ 
	int length = 1; /* 初始化子序列长度 */
	ElementType *TmpA;
	TmpA = malloc( N * sizeof( ElementType ) ); 
	if ( TmpA != NULL ) { 
		while( length < N ) { 
			Merge_pass( A, TmpA, N, length );
			length *= 2;
			Merge_pass( TmpA, A, N, length ); 
			length *= 2;
		}
		free( TmpA ); 
	} 
	else Error( “空间不足" ); 
}

算法优缺点：

优点：
它的平均复杂度是$O(NlogN)$，最坏时间复杂度也是$O(NlogN)$，而且它还是稳定的。
缺点：
需要额外的空间，并且需要在两个数组之间来回去复制元素。
用途：Merge_sort基本上不被用于做内排序，在外排序的时候它是一个非常有用的工具

C语言代码：归并排序-递归实现

/* 归并排序 - 递归实现 */

/* L = 左边起始位置, R = 右边起始位置, RightEnd = 右边终点位置*/
void Merge( ElementType A[], ElementType TmpA[], int L, int R, int RightEnd )
{ /* 将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 */
     int LeftEnd, NumElements, Tmp;
     int i;
     
     LeftEnd = R - 1; /* 左边终点位置 */
     Tmp = L;         /* 有序序列的起始位置 */
     NumElements = RightEnd - L + 1;
     
     while( L <= LeftEnd && R <= RightEnd ) {
         if ( A[L] <= A[R] )
             TmpA[Tmp++] = A[L++]; /* 将左边元素复制到TmpA */
         else
             TmpA[Tmp++] = A[R++]; /* 将右边元素复制到TmpA */
     }

     while( L <= LeftEnd )
         TmpA[Tmp++] = A[L++]; /* 直接复制左边剩下的 */
     while( R <= RightEnd )
         TmpA[Tmp++] = A[R++]; /* 直接复制右边剩下的 */
         
     for( i = 0; i < NumElements; i++, RightEnd -- )
         A[RightEnd] = TmpA[RightEnd]; /* 将有序的TmpA[]复制回A[] */
}

void Msort( ElementType A[], ElementType TmpA[], int L, int RightEnd )
{ /* 核心递归排序函数 */ 
     int Center;
     
     if ( L < RightEnd ) {
          Center = (L+RightEnd) / 2;
          Msort( A, TmpA, L, Center );              /* 递归解决左边 */ 
          Msort( A, TmpA, Center+1, RightEnd );     /* 递归解决右边 */  
          Merge( A, TmpA, L, Center+1, RightEnd );  /* 合并两段有序序列 */ 
     }
}

void MergeSort( ElementType A[], int N )
{ /* 归并排序 */
     ElementType *TmpA;
     TmpA = (ElementType *)malloc(N*sizeof(ElementType));
     
     if ( TmpA != NULL ) {
          Msort( A, TmpA, 0, N-1 );
          free( TmpA );
     }
     else printf( "空间不足" );
}

C语言代码：归并排序-循环实现

/* 归并排序 - 循环实现 */
/* 这里Merge函数在递归版本中给出 */

/* length = 当前有序子列的长度*/
void Merge_pass( ElementType A[], ElementType TmpA[], int N, int length )
{ /* 两两归并相邻有序子列 */
     int i, j;
      
     for ( i=0; i <= N-2*length; i += 2*length )
         Merge( A, TmpA, i, i+length, i+2*length-1 );
     if ( i+length < N ) /* 归并最后2个子列*/
         Merge( A, TmpA, i, i+length, N-1);
     else /* 最后只剩1个子列*/
         for ( j = i; j < N; j++ ) TmpA[j] = A[j];
}

void Merge_Sort( ElementType A[], int N )
{ 
     int length; 
     ElementType *TmpA;
     
     length = 1; /* 初始化子序列长度*/
     TmpA = malloc( N * sizeof( ElementType ) );
     if ( TmpA != NULL ) {
          while( length < N ) {
              Merge_pass( A, TmpA, N, length );
              length *= 2;
              Merge_pass( TmpA, A, N, length );
              length *= 2;
          }
          free( TmpA );
     }
     else printf( "空间不足" );
}