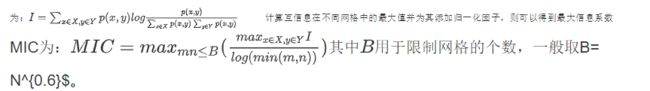毕业设计 医学数据分析 人体肠道细菌数据分析

---

0 前言

这两年开始毕业设计和毕业答辩的要求和难度不断提升，传统的毕设题目缺少创新和亮点，往往达不到毕业答辩的要求，这两年不断有学弟学妹告诉学长自己做的项目系统达不到老师的要求。

为了大家能够顺利以及最少的精力通过毕设，学长分享优质毕业设计项目，今天要分享的是

大数据医学数据分析 - 人体肠道细菌数据分析

学长这里给一个题目综合评分(每项满分5分)

• 难度系数：3分
• 工作量：3分
• 创新点：4分

选题指导, 项目分享：

https://gitee.com/dancheng-senior/project-sharing-1/blob/master/%E6%AF%95%E8%AE%BE%E6%8C%87%E5%AF%BC/README.md

1 课题背景

关于人体肠道细菌的研究表明，肠道菌群与人体的年龄、健康状况、饮食习惯等都存在关联，为了比较精确的探寻肠道菌群与人体年龄的关系，我们基于肠道细菌2388 个微生物特征(OTUs 和genus) 以及1638 个样本数据(重庆、泉州样本) 进行数据分析。

分析目标

• 对2000 多人的肠道细菌16S 数据进行初步探索, 将原始数据整合成具有分析意义的数据。
• 对数据进行特征分析, 筛选出一些能有效预测人体年龄的特征。
• 通过前期处理后的数据, 建立一个合理模型, 使之具有很好的预测效果。

2.数据预处理

导入工具包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

预处理

path = './data'

databg = pd.read_csv(path+'/2054samples backgroud information.csv')
datagenus = pd.read_csv(path+'/2054samples profiling of genus.csv')
dataotu = pd.read_csv(path+'/2054samples profiling of OTUs.csv')

databg = databg.iloc[:,0:18]

databg = databg[(databg['Sampled Loci'] == 'chongqing')|(databg['Sampled Loci'] == 'quanzhou')]

datagenus = pd.merge(databg,datagenus,on = 'SampleID',how = 'inner')

dataotu = pd.merge(databg,dataotu,on = 'SampleID',how = 'inner')

缺失值情况

databg.isnull().sum()  #q缺失值情况

datagenus.isnull().sum()[datagenus.isnull().sum()!=0]

dataotu.isnull().sum()[dataotu.isnull().sum()!=0]

3 数据可视化

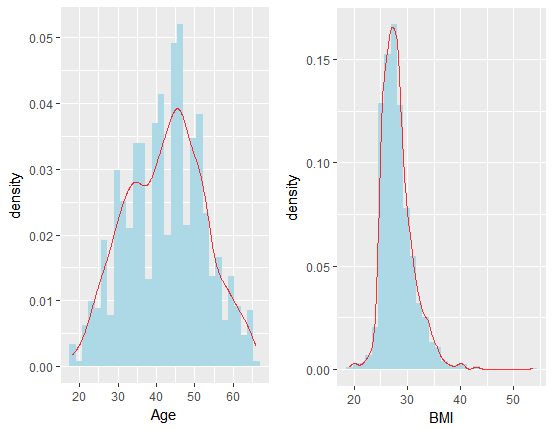
要研究因变量年龄(或BMI) 与肠道细菌之间的联系以及更好地进行预测，则有必要对年龄指标进行可视化分析，下图展示了年龄以及BMI 指标的分布情况：

从上图中可看出，年龄数据的取值在18 与66 之间，分布主要集中在35-50 岁之间，而BMI 数据则更为集中，BMI 指数主要集中在27 左右；因此从一定程度上可说明预测年龄的均方误差比预测BMI 更大；但是从另一个角度来说，BMI 数据与年龄数据存在一定的正相关关系，因此我们最终把年龄作为主要研究对象进行分析。

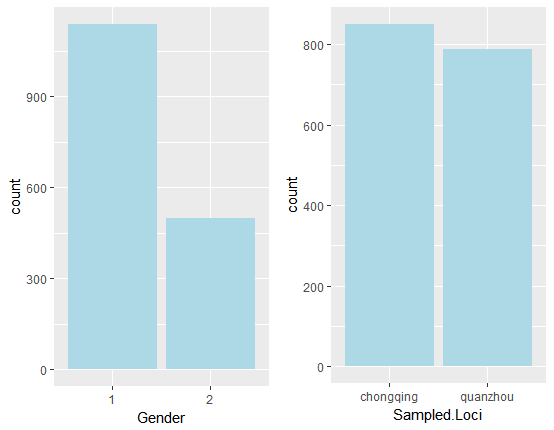
下图展示了背景信息中两个离散变量的分布情况：

从上图发现来自重庆地区的样本和泉州地区的样本数量相当。而性别变量，性别1 的数量则是性别2 数量的一倍之多。
细菌数据总共包含了2388 个特征，但大多数特征对预测年龄是几乎没有帮助的，并且特征数量过多对后续模型的精度均有较大影响，因此我们必须进行有效的特征筛选。

下面是实现数据可视化的R代码：

multiplot <- function(..., plotlist=NULL, file, cols=1, layout=NULL) {
  library(grid)
  
  # Make a list from the ... arguments and plotlist
  plots <- c(list(...), plotlist)
  
  numPlots = length(plots)
  
  # If layout is NULL, then use 'cols' to determine layout
  if (is.null(layout)) {
    # Make the panel
    # ncol: Number of columns of plots
    # nrow: Number of rows needed, calculated from # of cols
    layout <- matrix(seq(1, cols * ceiling(numPlots/cols)),
                     ncol = cols, nrow = ceiling(numPlots/cols))
  }
  
  if (numPlots==1) {
    print(plots[[1]])
    
  } else {
    # Set up the page
    grid.newpage()
    pushViewport(viewport(layout = grid.layout(nrow(layout), ncol(layout))))
    
    # Make each plot, in the correct location
    for (i in 1:numPlots) {
      # Get the i,j matrix positions of the regions that contain this subplot
      matchidx <- as.data.frame(which(layout == i, arr.ind = TRUE))
      
      print(plots[[i]], vp = viewport(layout.pos.row = matchidx$row,
                                      layout.pos.col = matchidx$col))
    }
  }
}
#使用示例multiplot(p1,p2,p3,p4,cols=xxx)
library(ggplot2)
path = 'F:/研习部/第二次案例分析/肠道16S测序数据/'
databg = read.csv(paste0(path,'2054samples backgroud information.csv'))
databg = databg[,-((ncol(databg)-3):ncol(databg))]
databg = databg[databg$Sampled.Loci %in% c('chongqing','quanzhou'),]
databg$Gender<-as.factor(databg$Gender)
databg$Sampled.Loci<-as.factor(databg$Sampled.Loci)
#年龄分布图
p1<-ggplot(data = databg)+geom_histogram(aes(x = Age,y = ..density..),fill = 'lightblue')+
  stat_density(aes(x = Age),geom = 'line',position = 'identity',color = 'red',alpha = 0.8)
#BMI
p2<-ggplot(data = databg)+geom_histogram(aes(x = BMI,y = ..density..),fill = 'lightblue')+
  stat_density(aes(x = BMI),geom = 'line',position = 'identity',color = 'red',alpha = 0.8)
#性别
p3<-ggplot(data = databg)+geom_bar(aes(x = Gender),fill = 'lightblue')
#腰围
p4<-ggplot(data = databg)+geom_histogram(aes(x = Waistline,y = ..density..),fill = 'lightblue')+
  stat_density(aes(x = Waistline),geom = 'line',position = 'identity',color = 'red',alpha = 0.8)
#sp
ggplot(data = databg)+geom_histogram(aes(x = SP,y = ..density..),fill = 'lightblue')+
  stat_density(aes(x = SP),geom = 'line',position = 'identity',color = 'red',alpha = 0.8)
#dp
ggplot(data = databg)+geom_histogram(aes(x = DP,y = ..density..),fill = 'lightblue')+
  stat_density(aes(x = DP),geom = 'line',position = 'identity',color = 'red',alpha = 0.8)
#fbg
ggplot(data = databg)+geom_histogram(aes(x = FBG,y = ..density..),fill = 'lightblue')+
  stat_density(aes(x = FBG),geom = 'line',position = 'identity',color = 'red',alpha = 0.8)
#胆固醇
p5<-ggplot(data = databg)+geom_histogram(aes(x = Cholesterol,y = ..density..),fill = 'lightblue')+
  stat_density(aes(x = Cholesterol),geom = 'line',position = 'identity',color = 'red',alpha = 0.8)
#甘油三酯
p6<-ggplot(data = databg)+geom_histogram(aes(x = Triglyceride,y = ..density..),fill = 'lightblue')+
  stat_density(aes(x = Triglyceride),geom = 'line',position = 'identity',color = 'red',alpha = 0.8)
#ldl
ggplot(data = databg)+geom_histogram(aes(x = LDL,y = ..density..),fill = 'lightblue')+
  stat_density(aes(x = LDL),geom = 'line',position = 'identity',color = 'red',alpha = 0.8)
#hdl
ggplot(data = databg)+geom_histogram(aes(x = HDL,y = ..density..),fill = 'lightblue')+
  stat_density(aes(x = HDL),geom = 'line',position = 'identity',color = 'red',alpha = 0.8)
#ua
ggplot(data = databg)+geom_histogram(aes(x = UA,y = ..density..),fill = 'lightblue')+
  stat_density(aes(x = UA),geom = 'line',position = 'identity',color = 'red',alpha = 0.8)
#肌酐
ggplot(data = databg)+geom_histogram(aes(x = Creatinine,y = ..density..),fill = 'lightblue')+
  stat_density(aes(x = Creatinine),geom = 'line',position = 'identity',color = 'red',alpha = 0.8)
#egfr
ggplot(data = databg)+geom_histogram(aes(x = eGFR,y = ..density..),fill = 'lightblue')+
  stat_density(aes(x = eGFR),geom = 'line',position = 'identity',color = 'red',alpha = 0.8)
#位置
p6<-ggplot(data = databg)+geom_bar(aes(x = Sampled.Loci),fill = 'lightblue')
multiplot(p1,p2,cols = 2)
multiplot(p3,p6,cols = 2)

4 特征工程

首先利用最大信息系数和距离相关系数这两个统计量对特征进行初步的筛选，再对得到的特征集合利用递归的XGBOOST 模型，得到最优的特征子集。

人工预先筛选

ndep = databg.shape[1]

dataotu.head()

最大信息系数MIC

最大信息系数对于一般的变量之间关系具有普适效应，不仅可以发现变量之间的线性关系，也可以发现变量之间的非线性关系。
最大信息系数的计算方式完全基于互信息的计算方式。对于两个连续型随机变量，首先将其所在的二维空间使用m 乘以n 的网格划分，则可以将落在第$(x,y)$ 格子中的数据点的频率作为$p(x,y)$ 的估计：

\begin{equation}
p(x,y) = \frac{n_{x,y}}{N}
\end{equation}

其中$n_{x,y}$为格子$(x,y)$中的数据个数，$N$为总样本数。

则根据互信息量的计算公式，可以得到随机变量$X$，$Y$ 的互信息$I$ 为：

将Age作为因变量，对genus数据集和otu数据集中的所有变量计算与年龄的MIC，并绘制成散点图：

index1 = list(range(ndep,datagenus.shape[1]))
index2 = list(range(ndep,dataotu.shape[1]))

from minepy import MINE
def calmic(a,b):
    m = MINE()
    m.compute_score(a,b)
    return m.mic()
MIC1 = []
MIC2 = []
for i in range(ndep,datagenus.shape[1]):
    MIC1.append(calmic(datagenus['Age'],datagenus.iloc[:,i]))
for i in range(ndep,dataotu.shape[1]):
    MIC2.append(calmic(dataotu['Age'],dataotu.iloc[:,i]))

fig1 = plt.figure()
fig2 = plt.figure()
ax1 = fig1.add_subplot(1,1,1)
ax1.scatter(range(len(MIC1)),MIC1)
fig1.savefig('F:/研习部/第二次案例分析/ElegantNote 2.00/image/c1.png')
ax2 = fig2.add_subplot(1,1,1)
ax2.scatter(range(len(MIC2)),MIC2)
fig2.savefig('F:/研习部/第二次案例分析/ElegantNote 2.00/image/c2.png')

从上面两张图（第一张为数据集genus的$MIC$，第二张为数据集otu的$MIC$）可以看到，大部分特征的MIC值都十分集中，接近于0(即与Age没有明显的联系)。若将MIC值等于0.04作为阈值，可以发现大于该值的特征数量较少，MIC值均较大，与MIC值小于0.04的特征有明显的分化趋势。因此将$MIC=0.04$作为筛选特征的一个衡量标准。

距离相关系数dcorr

与最大信息系数类似，距离相关系数也是用于衡量特征之间相关性的一个统计量，且其具有较好的鲁棒性。

距离相关系数也是介于0与1之间的统计量。距离相关系数为0，说明两个特征之间相互独立，相反其值越大，说明两个特征之间的相关程度越大。

依旧是将Age作为因变量，对genus数据集和otu数据集中的所有变量计算与年龄之间的最大相关系数，并将最大相关系数绘制成散点图如下图所示。

from scipy.spatial.distance import pdist, squareform
import numpy as np
def distcorr(X, Y):
    X = np.atleast_1d(X)
    Y = np.atleast_1d(Y)
    if np.prod(X.shape) == len(X):
        X = X[:, None]
    if np.prod(Y.shape) == len(Y):
        Y = Y[:, None]
    X = np.atleast_2d(X)
    Y = np.atleast_2d(Y)
    n = X.shape[0]
    if Y.shape[0] != X.shape[0]:
        raise ValueError('Number of samples must match')
    a = squareform(pdist(X))
    b = squareform(pdist(Y))
    A = a - a.mean(axis=0)[None, :] - a.mean(axis=1)[:, None] + a.mean()
    B = b - b.mean(axis=0)[None, :] - b.mean(axis=1)[:, None] + b.mean()
    
    dcov2_xy = (A * B).sum()/float(n * n)
    dcov2_xx = (A * A).sum()/float(n * n)
    dcov2_yy = (B * B).sum()/float(n * n)
    dcor = np.sqrt(dcov2_xy)/np.sqrt(np.sqrt(dcov2_xx) * np.sqrt(dcov2_yy))
    return dcor

dcorr1 = []
dcorr2 = []
for i in range(ndep,datagenus.shape[1]):
    dcorr1.append(distcorr(datagenus['Age'],datagenus.iloc[:,i]))
for i in range(ndep,dataotu.shape[1]):
    dcorr2.append(distcorr(dataotu['Age'],dataotu.iloc[:,i]))

fig1 = plt.figure()
fig2 = plt.figure()
ax1 = fig1.add_subplot(1,1,1)
ax1.scatter(range(len(dcorr1)),dcorr1)
ax2 = fig2.add_subplot(1,1,1)
ax2.scatter(range(len(dcorr2)),dcorr2)
fig1.savefig('F:/研习部/第二次案例分析/ElegantNote 2.00/image/c3.png')
fig2.savefig('F:/研习部/第二次案例分析/ElegantNote 2.00/image/c4.png')

从上图（第一张为数据集genus的$dcor$，第二张为数据集otu的$dcor$）可以看到，大部分特征的最大相关系数值都十分集中，接近于0(即与Age没有明显的联系)。若将$dcor$值等于0.06作为阈值，可以发现大于该值的特征数量较少，$dcor$值均较大，与$dcor$值小于0.06的特征有明显的分化趋势。因此将$dcor=0.06$也作为筛选特征的一个衡量标准。

筛选 MIC是0.04，dcorr是0.06 逻辑关系是且(或 也可以尝试)

select_index1 = [index1[i] for i in range(len(index1)) if (MIC1[i]>0.04 and dcorr1[i]>0.06)] #or
select_index2 = [index2[i] for i in range(len(index2)) if (MIC2[i]>0.04 and dcorr2[i]>0.06)] #or

print(len(select_index1),len(select_index2))

递归xgboost

XGBOOST

前面两个小节将最大信息系数值大于0.04以及最大相关系数值大于0.06的特征初步筛选出来，作为与因变量年龄有一定相关关系的特征来进一步研究。在数据集genus中总共选出了18个特征，在数据集otu中总共选出了70个特征。

为了进一步研究肠道细菌特征和年龄之间的关系，找到具有更好预测效果的变量，本文将XGBOOST模型${}^{[2]}$作为基模型，采用递归的方式对特征进行进一步筛选。

XGBOOST是一种集成学习算法，每一个子树是一棵CART树。每一棵子树利用基尼纯度来衡量每一个特征的重要性，并且以此来选择分裂特征，而某个特征在所有子树中作为分裂结点的出现次数就是其对应的特征重要性。

本文将年龄作为因变量，将之前筛选出的88个特征作为输入，得到的特征重要性如下图所示(为了清楚的展示得分概况，下图只随机选取了20个特征来作为样例)：

##考虑AGE是响应变量
datagenus.head()
dataxgb = pd.merge(datagenus.iloc[:,[0,2]+select_index1],dataotu.iloc[:,[0]+select_index2],on = 'SampleID',how = 'inner')

dataxgb.head()

import xgboost as xgb
from sklearn.feature_selection import RFE
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
Y = dataxgb.iloc[:,1]
X = dataxgb.iloc[:,2:]

model = xgb.XGBRegressor()
model.fit(X.iloc[:,list(set(np.random.randint(0,X.shape[1]+1,20)))],Y)
from xgboost import plot_importance  #画出重要性图片
plot_importance(model)
fig=plt.gcf()
fig.savefig('F:/研习部/第二次案例分析/ElegantNote 2.00/image/c5.png')

递归筛选

在选择XGBOOST为基模型后，利用递归筛选的方式来选择最优的特征子集。即初始子集是原始特征集合(包含88个特征)，每次删去当前集合中一个最不重要的特征，利用3折交叉验证计算模型的预测得分。最终选取得分最高的子集作为最终的特征集合，具体算法流程算法一所示：

算法一：递归筛选特征
step1：初始特征集合为F
step2: 选出其中最不重要的特征$F_i$，并且记录此时的模型得分$s$
step3: 将特征集合更新为$F-F_i$，跳转回step2直至$F=\varnothing$
step4: 根据记录的模型得分选出最优得分对应的集合作为最终特征集合$S$

将88个特征输入算法，最终筛选得到39个特征，genus数据集包含7个特征，otu数据集包含32个特征。这些特征如下表所示(列举15个)：

重要特征（列举15个）
Alistipes Anaerostipes Blautia Otu67 Otu68
Erysipelatoclostridium Granulicatella Otu10 Otu8 Otu80
Salmonella Turicibacter Otu119 Otu102 Otu99

由于genus数据集与otu数据集是按照两种方式来分类细菌的，因此两个数据集中的特征会有所重合，而重合的特征会使得数据噪声增加，使模型产生过拟合现象。因此本文对筛选得到的39个特征利用特征注释表进行人工查重，发现此39个特征未包含重复特征。

def  rec_select(a,b): #定义递归选取变量的函数，每次删去最不重要的变量，直至删完，选取精度最好的子集
    global ans
    ans = []
    for i in range(a,b+1): #a
        model = xgb.XGBRegressor()
        selector = RFE(estimator=model, n_features_to_select=i) #特征选取数量从小到大
        X_choice = selector.fit_transform(X, Y) #选出新的数据集
        X_train, X_test, Y_train, Y_test = train_test_split(X_choice,Y,test_size=0.3, random_state=0)
        ans.append(np.mean(cross_val_score(model,X_choice,Y,cv = 3))) #交叉验证作为得分
        if i%10==0:
            print(i)
    index = ans.index(max(ans))
    return list(range(a,b+1))[index]
rec_select(20,88)

selector = RFE(estimator=model, n_features_to_select=39)
selector.fit(X, Y)
selector.support_

X.iloc[:,selector.support_].head()

5 神经网络模型

网络的架构

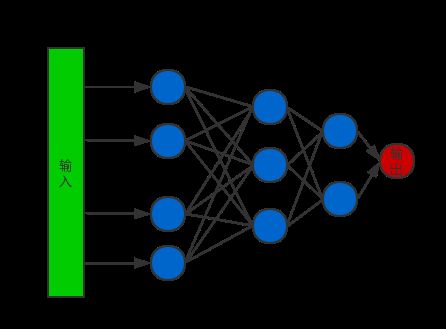
本文选择只包含全连接层的神经网络并且结合dropout层来进行年龄预测。网络示例如下图所示：

为了使样本各个特征的比重相同，且使得神经网络的反向传播算法得以很好的收敛，本文首先对数据进行如下处理：

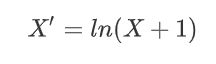
其中$X$表示特征数据集，随后再对数据进行归一化处理。

超参数的确定

在确定完网络架构后，模型依旧有几个重要的超参数需要确定。

学习率的确定，学习率需要根据模型的输出结果手动调节，若模型损失函数变化很小，则需要适当调大学习率，若模型损失函数反复变化，则需要降低学习率，并采用自适应学习率，本文设置为0.001。

学习批次的确定，由于样本量较大，若完整训练的数据集再更新权重会耗费大量运算时间，选择训练批次是合理的解决方法，一般批次大小取2的指数次方倍，本文的批次设置为32,64,128或256。从中选取损失最小的值作为最终批次，经过参数调试选择256为训练批次。

迭代次数的确定，一般选取若继续增大迭代次数时，损失函数继续下降而测试集上误差却上升的最小的迭代次数，本文选取为100。

模型层数的确定，层数设定为3层，对于卷积神经网络更多的隐藏层意味着更强的解释能力，但对于全连接层网络，更深的层对网络解释能力帮助并不大，但是3层网络普遍优于2层网络。

隐藏层结点数确定，一般将隐藏层结点数设置为一个大于输入值的数，本文将三个隐藏层结点数均设置为64。

激活函数的确定，本文的输出层利用Relu函数来激活，三个隐藏层的激活函数均使用PRelu函数来激活。

Dropout层丢弃率的确定，为了防止网络过拟合，为每一个隐藏层再加上Dropout层，即每一次训练时随机丢弃该层中一定比例的神经元，丢弃率本文设置为0.2

网络权重的初始值均采0与1之间的均匀分布。

6 结果与讨论

模型结果

将特征工程处理后的数据带入神经网络模型训练，并进行10折交叉验证，将平均绝对误差(MAE)作为损失衡量标准。最终得到的误差为6.81岁。为了更客观的考量预测结果的合理性，本文分别计算了训练数据集年龄与BMI的相关系数以及预测年龄与对应BMI的相关系数，分别为0.224与0.152。可以看到两者都呈现一定的正相关关系，预测结果很好的保持了数据原有的性质。

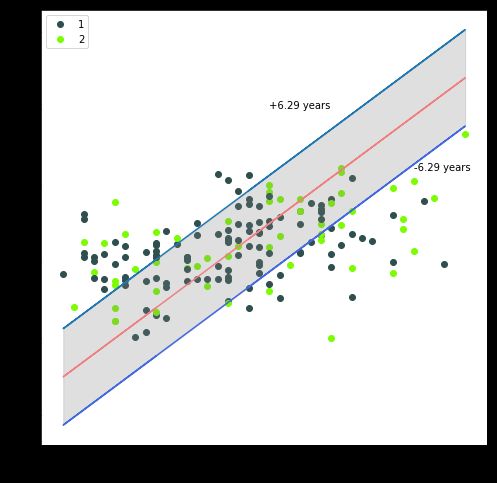
取交叉验证中的某一测试数据集来进行可视化，将真实年龄作为横坐标，预测年龄作为纵坐标，并将真实年龄作为基准线，再考虑预测样本之间的性别差异，画出预测散点图:

从上图中可以看到大多数样本点都落在平均误差的范围内，有一部分点的预测误差较大，误差大于平均意义上的6.29岁。且这些样本点主要集中在30岁以下和55岁以上的样本，这与训练数据集两端年龄的样本数量不足有关。同时也可以发现不同的性别其年龄预测的结果大致相同，性别这一变量并不会对年龄的预测产生重大影响。

若考虑预测样本地区之间的差异，预测散点图如下图所示：

从上图可以发现，对于50岁以上的样本，对于重庆地区的年龄预测误差要比泉州地区的预测误差更大。若要继续提高预测精度，可以考虑对50岁以上的样本进行分地区预测。

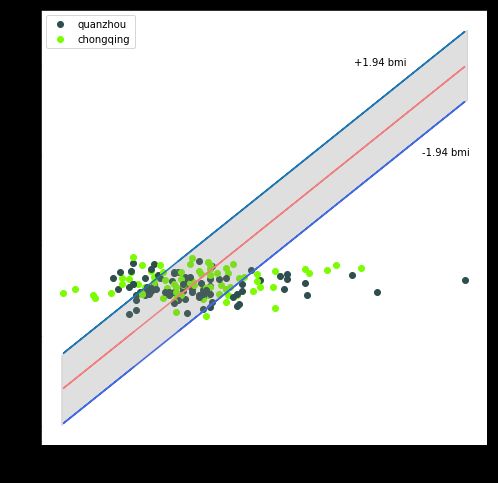
由于BMI变量也具有重要的实际意义，因此本文也将BMI变量作为因变量，采用同样的模型进行特征筛选和数据训练，最终的预测误差(MAE)为1.94，结果也较为理想，其预测结果如下图所示(BMI的高预测精度主要源于其数据方差较小，年龄数据分布的标准差为10.1，而BMI数据分布的标准差3.01，仅为年龄标准差的三分之一！)

连续SMOTE上采样

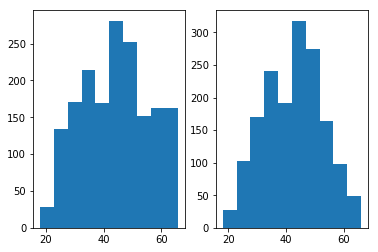
将利用特征工程小节中的方法筛选得到的数据划分为训练集与测试集，并且画出训练数据的年龄数据分布，如下图右图所示：

通过上图右图可以发现，样本数据主要集中在30-55这个年龄段，可以预见到如此的训练样本分布会导致最终的预测结果也会集中分布在这个年龄段，从而无法很好预测30岁以下，55岁以上的样本。

为了解决这一问题，对训练集合中29岁以下，58岁以上的样本进行了SMOTE过采样^{[1]}的方式(采样时将年龄也归入自变量一同进行采样)，近邻样本数选取为5个。最后得到的数据分布如上图左图所示。

经过上采样，各年龄段的样本分布明显均匀了很多，这也有利于模型做出更为合理的判断。

模型比较

将利用上采样数据集训练的模型(所有人工生成数据均未落入测试集中)与利用原始数据训练的模型进行比较，其结果如表：

数据集	MAE	预测值域
SMOTE上采样数据集	6.81	$[28.9,60.1]$
原始数据集	6.81	$30.1,56.6$

可以看到尽管SMOTE上采样未对模型的预测精度有所改进，却使得模型的预测值域更大。而在精度相同的情况下，我们更希望获得一个有更多响应情况的模型，这也证明了进行SMOTE上采样的合理性。

本文的训练特征既包含了genus数据集中的特征，又包含了OTU数据集中的特征，将训练结果与使用单独数据集的训练结果进行对比，如下表所示：

数据集	MAE
Genus数据集	8.03
Otu数据集	7.14
合并数据集	6.81

从上表中可以看到，模型在合并训练集上得到的预测精度最高。因此与年龄相关的细菌类别并不一定是基于一种分类方式得到的类别的，可能与多种分类方式的多个细菌类别息息相关。

将模型与其他模型进行横向对比，结果如下表所示：

模型	MAE(原始数据集)	MAE(采样数据集)
神经网络	6.81	6.81
随机森林	8.25	8.61
XGBOOST	7.83	8.83
线性回归	7.80	9.22

可以看到与一些常用模型比较，本文的预测精度拥有较为明显的优势。

7 最后