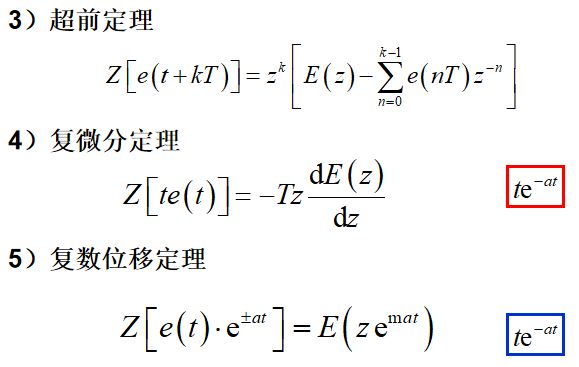自动控制原理笔记-采样控制系统
目录
采样控制系统的基本概念:
采样过程及采样定理:
一、采样过程
二、采样定理(香农采样定理、奈奎斯特采样定律)
三、信号复现
四、零阶保持器
z变换与z反变换:
z变换的定义
z变换基本定理
z反变换
采样系统的数学模型
一、差分方程(时域)
二、脉冲传递函数的基本概念
脉冲传递函数的求法
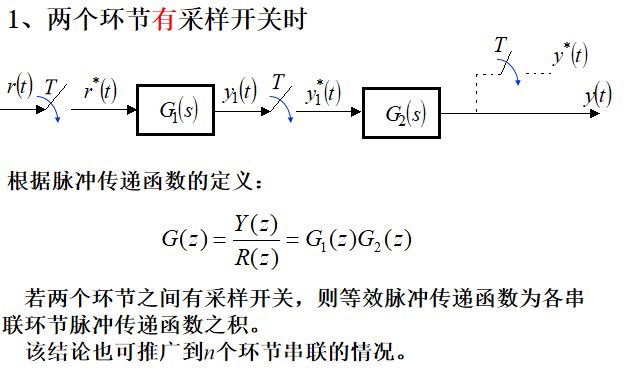
串联环节的脉冲传递函数
闭环系统的脉冲传递函数
采样系统的稳定性
稳定性的基本概念
稳定的充要条件
s平面与z平面的映射关系
线性采样系统的劳斯判据
采样系统的暂态性能分析
暂态响应与闭环极点位置的关系
采样系统的静(稳)态误差
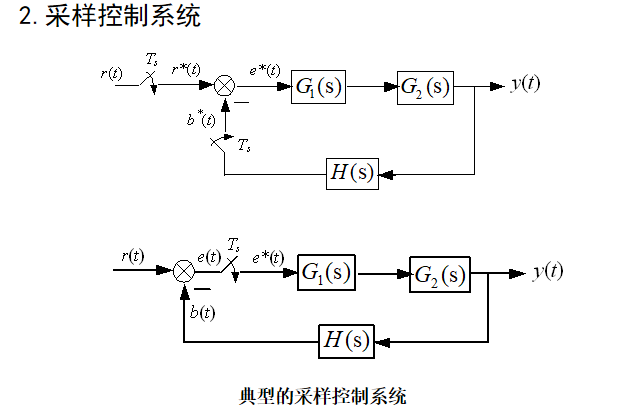
采样控制系统的基本概念:
连续(控制)系统:控制系统中的输入信号或变量随时间连续变化;
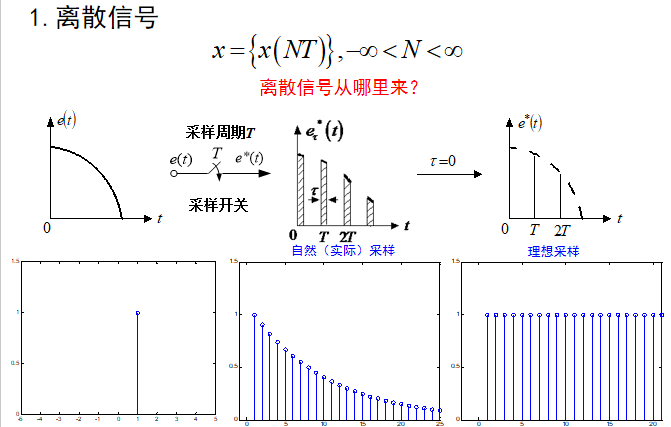
离散(控制)系统:控制系统中的输入信号或变量在时间上是离散的,即系统中仅包含脉冲信号或数字(数码)信号;
采样(控制)系统:控制系统中既包含连续信号,又包含离散信号。
采样过程及采样定理:
1、采样:连续信号经采样开关后变成离散信号的过程;
2、采样开关:实现采样的装置,又名采样器;
3、复现:将采样后的采样信号恢复为原来的连续信号的过程;
4、采样方式:
(1)等周期采样:采样时刻kT
(2)多阶采样:采样时间周期性重复
(3)多速采样:有两个以上不同采样周期的采样开关对信号同时进行采样
(4)随机采样:采样是随机进行的,没有固定的规律
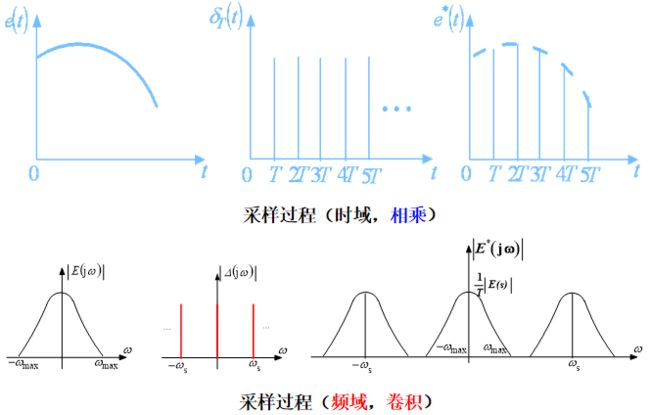
一、采样过程
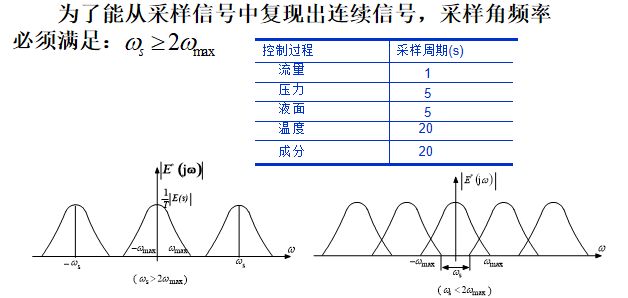
二、采样定理(香农采样定理、奈奎斯特采样定律)
采样定理的物理意义:满足采样定理的采样信号中,含有的连续信号信息可以通过低通滤波器复现出来。
三、信号复现
e*(t)为脉冲信号,频率丰富(含有多种高频分量),若直接加到系统上,相当于引入噪声干扰或损坏系统。在实际运用中,需要信号复现滤波器,使e*(t)复现为原连续信号。
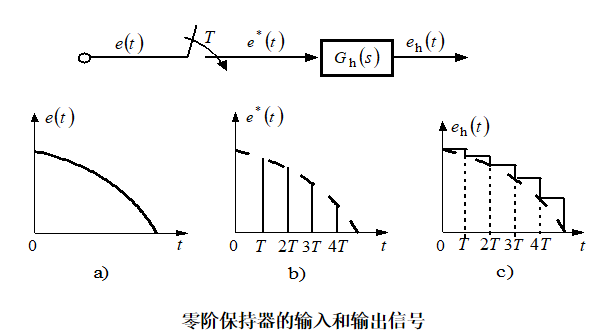
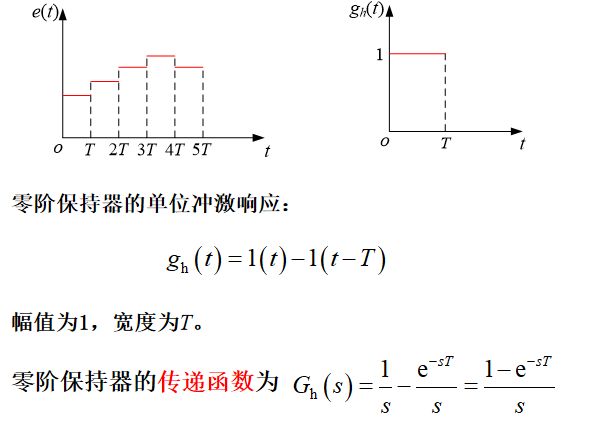
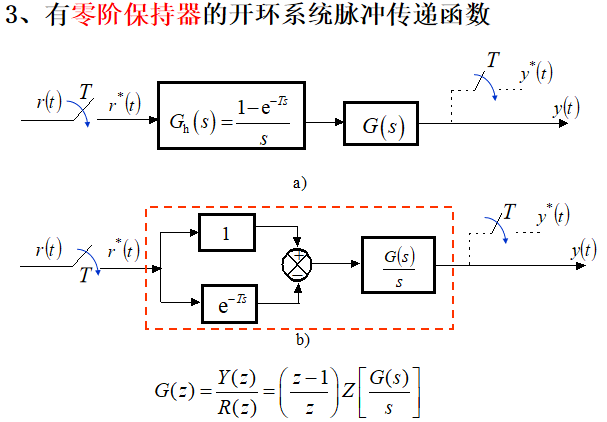
四、零阶保持器
从频域看:理想滤波器可以将采样信号恢复成连续信号,但物理上不可实现。因此要寻找一种物理上可实现、特性又接近于理想滤波器的设备——保持器。
从时域看:采样信号只在采样点上有定义, e*(kT)和e*(kT+T)都是有定义的,但是在这两者之间的时间段上连续信号应该是什么样子呢? 这就是保持器要解决的问题。
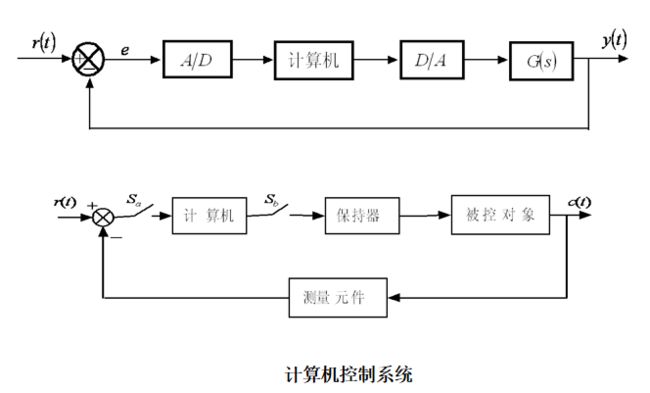
保持器是采样系统的一个基本单元,功能是将离散模拟信号恢复成连续信号。
从数学角度看:保持器是一种时域外推装置,作用机理是将过去时刻或现在时刻的采样值进行外推
z变换与z反变换:
z变换的定义
| 研究对象 |
数学描述 |
求解工具 |
性能评价 |
| 线性连续系统 |
微分方程 |
Laplace变换 |
稳 快 准 |
| 线性离散系统 |
差分方程 |
z变换 |
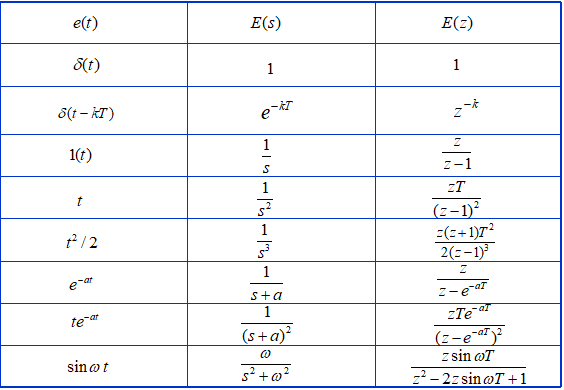
典型函数的z变换
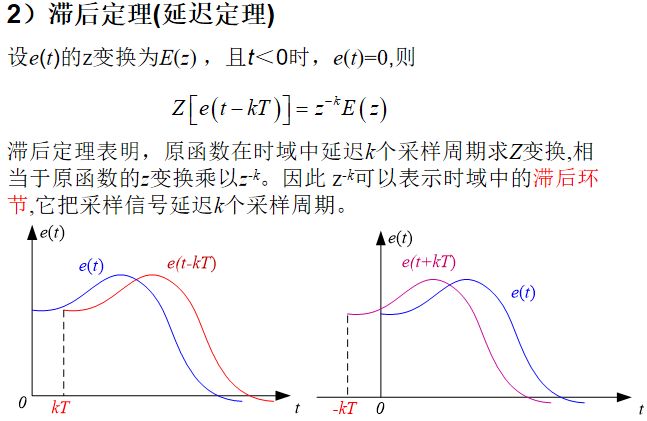
z变换基本定理
z反变换
采样系统的数学模型
一、差分方程(时域)
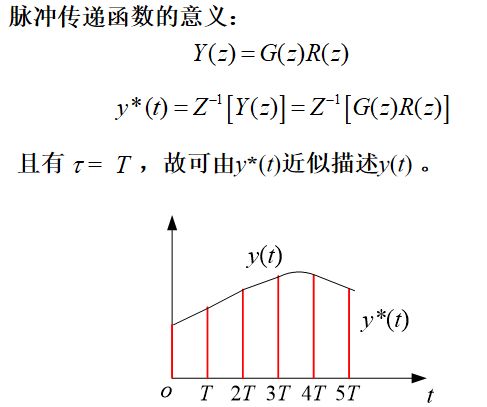
二、脉冲传递函数的基本概念
线性采样系统初始条件为零时,系统输出信号的z变换与输入信号的z变换之比,称为线性采样系统的脉冲传递函数,或称为z传递函数。
并非所有的离散系统均可以求出脉冲传递函数
实际采样控制系统的输出信号通常是连续信号,为了应用脉冲传递函数的概念,可在系统的输出端虚设一个同步采样开关,使输出成为采样信号。
脉冲传递函数和连续系统的传递函数一样表征了采样系统的固有特性;
它除了与系统的结构、参数有关外,还与采样开关在系统中的具体位置有关。
脉冲传递函数的求法
串联环节的脉冲传递函数
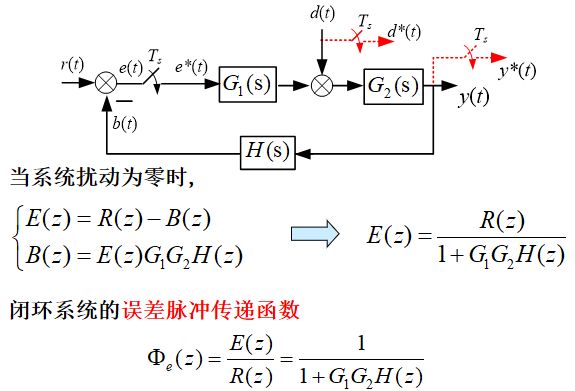
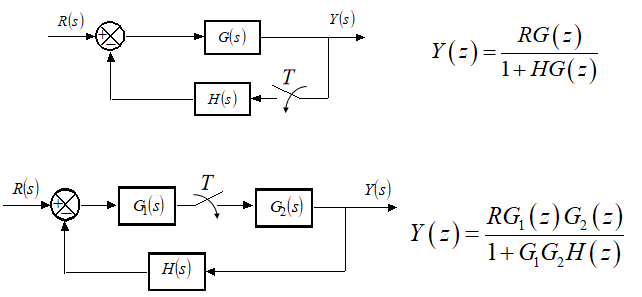
闭环系统的脉冲传递函数
对于有些采样控制系统,无法写出闭环脉冲传递函数只能写出输出的z变换
采样系统的稳定性
稳定性的基本概念
稳定性(stability)是指在扰动的作用下,系统会偏离平衡状态,在扰动撤除后,系统恢复到原平衡状态的能力; 根据稳定性的定义,可以采用脉冲响应的特性来研究系统的稳定性; 系统的脉冲响应如果能够衰减到零,则系统是稳定的;否则系统是不稳定的。
稳定的充要条件
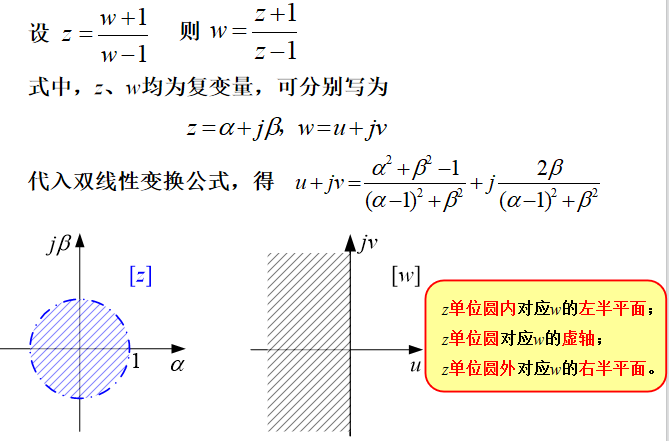
s平面与z平面的映射关系
| s左半平面 |
z平面单位圆内 |
||
| s平面的虚轴 |
z平面的单位圆 |
||
| s右半平面 |
z平面单位圆外 |
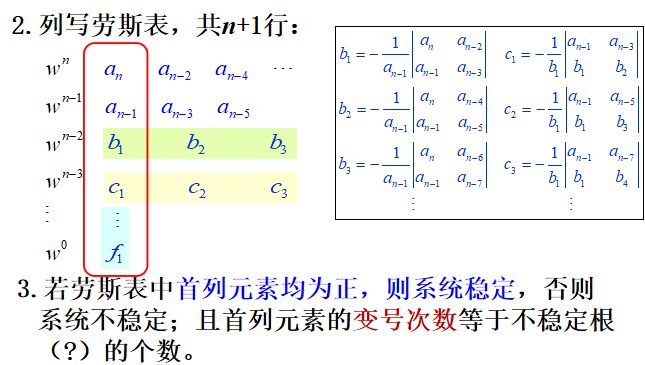
线性采样系统的劳斯判据
线性采样系统不能直接使用劳斯稳定判据,因为采样系统稳定边界是z平面上以原点为圆心的单位圆周,而不是虚轴。 为了能使用劳斯判据,可将z平面上单位圆周映射到新坐标系中的虚轴,这种变换称为w变换,或称双线性变换。
采样系统的暂态性能分析
采样系统的单位阶跃响应
闭环采样系统的脉冲传递函数为
式中M(z)—闭环脉冲传递函数的分子多项式
D(z) —闭环脉冲传递函数的分母多项式
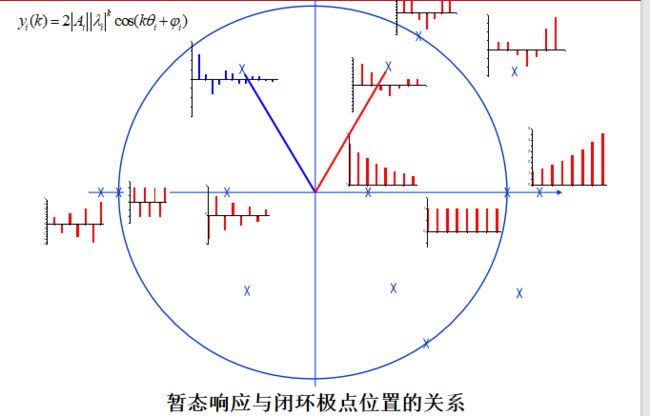
暂态响应与闭环极点位置的关系
1)当闭环脉冲传递函数的极点位于z平面上以原点为圆心的单位圆内时,其对应的暂态分量是衰减的。
2)要使控制系统具有比较满意的暂态响应,其闭环极点应尽量分布在z平面单位圆内的右半部,避免分布在单位圆内的左半部。
3)极点尽量靠近坐标原点,相应的暂态分量衰减速度较快。
4)离单位圆周最近且附近无闭环零点的共轭复数极点为主导极点。
采样系统的静(稳)态误差
采样系统是系统中一处或几处信号是采样信号的系统; 采样系统要用差分方程或脉冲传递函数去研究; z变换只能反映采样时刻的信息,因此要是采样信号能够真实地反映连续信号信息,采样过程要满足采样定理; 采样系统稳定的充分必要条件是闭环特征根位于复平面上的单位圆内; 可以通过双线性变换和劳斯判据判断高阶采样系统的稳定性; 采样系统的动态性能和静态性能分析。