理解生成对抗网络 GAN：Generative Adversarial Nets

引言

上一篇文章理解差分自动编码器 VAE：Variational AutoEncoder讲解了生成模型 VAE，VAE 为了估计 variational lower bound 的梯度，提出了 SGVB，理论上比较复杂且包含了很多近似和假设，GAN 也是一类生成模型，相比 VAE 在理论上更加直观，生成的样本质量也不错，因而受到大量研究者的关注。本文从数学角度分析了 GAN 的对抗损失究竟在学习什么，并解释了为什么 GAN 的训练不稳定。

---

GAN 简介

GAN 的目标是：给定潜在空间中任意一点 $z\in {\mathbb{R}}^d$，生成对应的尽可能逼真的数据 $x\in {\mathbb{R}}^D,d<D$。GAN 由生成器 G 和判别器 D 组成，G 的输入是随机变量 $z\sim p_z(z)$，输出是仿真数据 $G(z)\sim p_g(x)$，D 的输入是仿真数据和真实数据 $x\sim p_{data}(x)$，G 想要让生成数据的分布尽可能接近真实分布，而 D 想要尽可能准确地区分生成数据和真实数据，在对抗损失的驱动下，G 生成的数据越来越逼真，D 的判别能力也越来越强，理想情况下，D 最终将无法判别生成数据和真实数据。

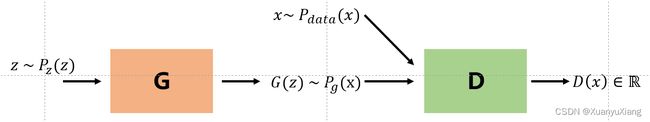
对抗损失

对抗损失如下：

${\min }_G{\max }_{D}V(G,D)={\mathbb{E}}_{x\sim p_{data}(x)}[logD(x)]+{\mathbb{E}}_{x\sim p_g(x)}[log(1-D(x))]$

直观上讲，首先训练 D 使 $V(G,D)$ 最大化，在此基础上固定 D 的参数，然后训练 G 使 $V(G,D)$ 最小化；从数学角度上讲，训练 D 使 $V(G,D)$ 最大化的过程就是在度量 $p_{data}(x)$ 和 $p_g(x)$ 之间的 JS 散度，训练 G 使 $V(G,D)$ 最小化的过程就是在减小 $p_{data}(x)$ 和 $p_g(x)$ 之间的 JS 散度。首先讨论 ${\max }_{D}V(G,D)$ 过程：

$V(G,D)$

$=\int p_{data}(x)logD(x)dx+\int p_g(x)log(1-D(x))dx$

$=\int [p_{data}(x)logD(x)+p_g(x)log(1-D(x))]dx$

想要让此项最大化，可以对积分中的项求导，取导数为 0 的点，所得点就是最佳 D：

$D\ast (x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$

将最佳 D 代入原对抗损失得：

$V(G,D^{\ast })$

$={\mathbb{E}}_{x\sim p_{data}(x)}[log\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}]+{\mathbb{E}}_{x\sim p_{data}(x)}[log\frac{p_g(x)}{p_{data}(x)+p_g(x)}]$

$=-2log2+2JS(p_{data}(x)||p_g(x))$

所以，当把 D 训练到最佳的时候，对抗损失表示的就是 $p_{data}$ 和 $p_g$ 之间的 JS 散度，此时固定 D 的参数来最小化对抗损失，就是在减小 JS 散度，使生成数据分布接近真实数据分布。

梯度消失问题

D 训练的越好，G 梯度消失越严重。JS 散度有一个性质：当两个分布没有重叠时，其 JS 散度总是常数 log2，而实际上，$p_{data}$ 和 $p_g$ 总是不重叠的，这是因为，当 $p_{data}$ 和 $p_g$ 的支撑集（support）是高维空间中的低维流形（manifold）时，$p_{data}$ 和 $p_g$ 重叠部分的测度（measure）为 0 的概率为 1，也就是说，尽管 $p_{data}$ 向 $p_g$ 接近了，但由于两者没有重叠，计算出来的对抗损失没变，所以没有产生梯度来更新 G 的参数。

模式坍塌问题

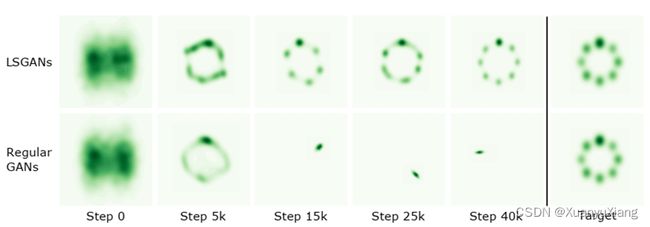
模式坍塌（mode collapse）是指不管 G 的输入是什么，输出总是不变，如下图所示，第二行出现了明显的模式坍塌问题。

在 GAN 原文中，作者为了让 G 在训练初始阶段拥有更大的梯度，将 G 的损失更改为：

${\mathbb{E}}_{x\sim p_g}[-logD(x)]$

中间的推导过程省略，这里直接给出结论（具体推导过程可以参考[1]）：

${\mathbb{E}}_{x\sim p_g}[-logD(x)]=KL(p_{data}||p_g)-2JS(p_{data}||p_g)$

可以看出，这个损失存在两个问题，一是要求最小化 KL 散度的同时最大化 JS 散度，这势必会带来训练的不稳定；二是由于 KL 散度是不对称散度，会引起模式坍塌问题：

$p_g\to 0,p_{data}\to 1,KL(p_g||p_{data})\to 0$

$p_g\to 1,p_{data}\to 0,KL(p_g||p_{data})\to \infty$

第一行错误对应的是“生成器没能生成真实的样本”，对应缺乏多样性，其惩罚微小；第二行错误对应的是“生成器生成了错误的样本” ，对应准确性，惩罚巨大，这不对称之下，生成器宁可多生成一些重复准确的样本，也不愿意去生成多样性的样本，这种现象就是大家常说的模式坍塌。

参考

[1] WGAN (原理解析)