209.长度最小的子数组（中等） 力扣数组刷题笔记（0）

 

 

0、题目描述：

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例：

输入：s = 7, nums = [2,3,1,2,4,3] 输出：2 解释：子数组 [4,3] 是该条件下的长度最小的子数组。

题目链接：力扣

1、题目理解：

题目要求求出数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。

如果不存在符合条件的子数组，返回 0。

1.1、题目分析及变量设置

返回值：如果存在，返回最小长度

              如果不存在，返回0，则可以设立  设立声明变量int result作为返回结果

        对数组长度进行操作 ：int len=nums.length求出长度必不可少

不管是两重for暴力搜索破解 还是 一重for循环加双指针 滑动窗口

他的最小长度，如果有，那就是动态更新的，此处声明变量 int sublen=0

还需要声明一个变量作为对子数组元素相加的和，与需要大于等于的目标值target进行比较

此处我们声明 Int sum=0；跟数组长度一样动态更新

然后 我们需要知道子数组是从哪个索引下标到哪个索引下标，才能求出长度

所有 int sublen=j-i+1;

                                        变量准备工作做好了：就可以coding了~

2、暴力破解

2.1、两重for循环

第一层for循环中的计数器i用来更新子数组的左边起始位置

第二层for循环中的计数器j用来更新子数组的从起始位置i开始搜索，不断加一 到满足sum>=tagret然后记录最小长度，退出 本次循环 之后再由第一层for循环中的I更新起始位置。再次进行搜索 

public static int solution(int[] nums,int target)
{
    int len=nums.length;
    int sum=0;
    int result=Integer.MAX_VALUE;
    int sublen=0;
    for(int i=0;i=target)
            {
                sublen=j-i+1;
                  break;
            }   
        }
    result=result

将result初始化结果赋值int最大值，与result=result

如果有这种子串，则在每一次更新时，都将result返回动态的最小的子数组长度sublen

如果没有子数组满足，最终result值为sublen的0

返回0

//此语句保证了，ret能返回一个大于等于0的值

2.2、 暴力破解总结分析

一：两重for循环，变量定义前要明白变量声明之后是用来干什么的，如何巧妙地赋值

二：for循环两层，变量的位置一定要摆对。如ruguo

for(i; ; )
{
    sum=0;
    for(j; ; )
    {
        if(sum>=target)
        //sum=0;
    }
}

如果sum=0没有在每次一更换起始位置，即子数组的左边就将其初始化赋值0

而是在每次找到满足sum>=target满足的之后放在if里初始化，那必定出bug

 如图所示，如最后 sum=4+5<11无法进入if进行初始化

再加上一个5 sum=4+5+5>11会出bug,此处属于逻辑错误。

2.3、 初识力扣中等难度题，浅谈心得

JAVA中常见的错误有三种 编译时错误（compiler error），运行时错误（runtime error），逻辑错误（logical error）逻辑错误是较难分析的，

但是每一次发现错误---->改正错误----->记得错在哪儿------>以后编程不犯错

这都是对自己能力的一种提升，

其实一开始我在if里面的break写的还是return result;

但是了解错误之后就发现这可不兴啊！宝友 ，你用一个break，纵然两层循环，写在内部，也只是断掉内层循环的当前循环，你写个return进去，不管多少层循环，满足条件直接给你终止返回破开了。岂不是直接裂开。

还有今日更文为什么要加上声明变量的理解，对一个算法题毫无头绪，不妨先把问题拆看，看看需要什么变量，什么数据结构，什么if while的判断条件，拆分成小问题，其实也有分而治之的思想。

3、小菜鸡以暴力破解浅谈力扣培养兴趣的方法

但是力扣其实简单题 无非就是 数组，链表，字符串及若干考察数学思想的题。

从数组来说

数组是很重要的数据结构且是非常重要的基础，力扣考察数组的简单题目一般在思维上都不难，主要是考察对代码的掌控能力

也就是说，想法很简单，但实现起来 可能就不是那么回事了。

首先要知道数组在内存中的存储方式，这样才能真正理解数组相关的面试题，从数组开始其实就有关于对象，引用，JVM中堆和栈的思想了，不理解的老铁可以看我之前关于数组知识的帖子。

3.1、总结

其实力扣上即使是中等题也有很大一部分可以直接暴力破解的，然后在做题的时候，不要好高骛远，先把问题拆看，看看需要什么变量，什么数据结构，什么if while的判断条件，拆分成小问题，然后尝试可不可以暴力，暴力超不超时，其实力扣上的超过多少人和时间空间复杂度的性能分析就是个小玩具，没必要刻意去追求。自己大致看一眼时o(n) 还是o(n^2)还是 o(logn)就行。

保持自己的进度，然后再进行算法的逐步优化，对复杂度精简。

4、以暴力破解简化入门双指针（滑动窗口）

 

左指针命名r（left）

右指针命名r（right） 

4.1 双指针与for的切换

变量还是那么多上述变量  一维数组其实就是一个连起来的单元格，掐头去尾就是两个指针就解决了 双指针直接节省一层循环，虽说暴力破解，唯for不破，可是双指针风骚起来，真没for循环什么事了。

4.1.1 在暴力破解中我们提到 

第一层for循环中的计数器i用来更新子数组的左边起始位置

第二层for循环中的计数器j用来更新子数组的从起始位置i开始搜索，不断加一 到满足sum>=tagret然后记录最小长度，退出 本次循环 之后再由第一层for循环中的I更新起始位置。再次进行搜索 

如果不满足子数组之和大于等于目标值，那就往右移动 

如果满足子数组之和大于等于目标值，那就换个起点搜索，看能不能找到更短的子数组

既然这样 何不把两层 for循环中的计数器i,j换成两个指针 然后 搜索子数组 

子数组大于目标值，左指针右移搜索

子数组小于目标值，左指针右移加上数字补充总和搜索 

那么右指针肯定有 范围 范围就是数组长度 

左指针一定小于等于右指针的位置。

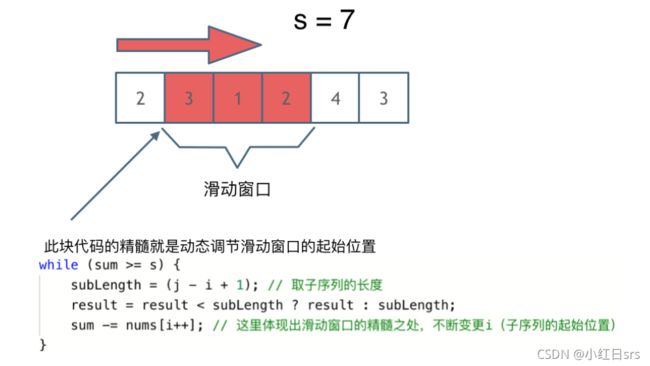
核心语句就是 

while(sum>=target)
{
    sublen=j-i+1;//求当前子数组的长度。
    sum-=sum[i++];//动态滑动窗口，左指针右移一位同时去掉原左指针指向的元素
    return result

for(int r=0;r

 

sum=sum[i] //sum从下标为0开始，小于目标值就不断加，或者左窗口收缩导致和（sum）小于目标值（target）之后，向右扩窗口补充。

  sum-=nums[l++];

其中 sum-=nums[l++];

可以拆分成 sum=sum-nums[l];

                        l++;//先向减去数组元素，再执行自加操作，左指针右移一位。

此处精髓三句话，有细节知识点要补充：

1：如本题中有取子序列的长度，老铁们对这种有指针长度位置的比较，一定要注意代码编写时的思维逻辑，如：先移动指针【++l】再减去指针对应的元素？

  sum-=nums[++l];

 还是先移动指针再求长度？代码的顺序问题就可能造成bug。

力扣目前做数组的简单题，中等题其实就只是锻炼细节，编程语言熟练性和知识点。还远没有达到DP动态规划，分治，回溯，BFS,DFS。加油啊老铁们，虽然只是一道中等难度里简单的题，可是也码不停蹄的打字，觉得有用的老铁还请支持。我们共同进步。

 

5、总结

一点一点，脚踏实地，共同进步吧，兄弟们！

日拱一卒，日有所进。

没有什么使我停留——除了目的，纵然岸旁有玫瑰、有绿荫、有宁静的港湾，我是不系之舟。