薪火相传，构建生态——记约束求解基础与应用训练营

导读：如今，「深度学习」已然成为了人工智能的代名词。然而，在人工智能「三起三落」的进程中，神经网络等联结主义技术一开始并不被看好。上世纪 90 年代初，符号主义学派占据了人工智能领域的半壁江山，人工智能研究者在物理符号系统假设和基于知识的启发式求解方法的指导下，研发出了一系列专家系统、数学规划应用。

01

艰难起步：一小拨儿人的坚守

彼时，华人学者在约束求解等符号主义方法的研究领域也开始崭露头角。例如，迁移学习、联邦学习领域的「宗师」杨强教授早年间就曾从事逻辑推理和规划方面的研究，其开发的开源规划软件「ABTWEAK」在工业界得到广泛应用，该成果被 AAAI 1990 收录。此外， 来自北京大学、清华大学、吉林大学、华中科技大学等国内高校的学者也在这一领域做出了一系列贡献。

然而，随着日本「第五代计算机」研发计划的失败，符号主义流派「由盛转衰」。到了 2011 年，如今的中科院软件所研究员蔡少伟去参加「可满足性判定的理论与应用国际会议」SAT 2011 时，他在会议上几乎找不到除自己之外的第二张中国面孔。一时间，约束求解领域的研究者陷入了「孤军奋战」的艰难处境。我国该领域的研究者开始了漫长的坚守！

实际上，这种现象不仅仅存在于中国的计算机学术界。运筹学大师叶荫宇教授的弟子、杉树科技创始人葛冬冬博士曾粗略估计：在世界范围内，精通求解器研发的人不超过二位数！相较于深度学习顶会的盛况空前，目前约束求解会议的规模则可谓「袖珍」。例如，每年 SAT 会议的参会者大约在 100 人左右，此类课题在 IJCAI、AAAI 等大型综合人工智能会议中的占比也十分有限。

约束求解器是一个复杂工程

02

工业软件之魂——约束求解

约束求解是形式化方法的重要组成部分，形式化方法基于严格的数理逻辑为设计、分析、验证计算系统提供规划约、分析验证和构造理论的方法。而约束求解则是面向通用问题的形式化方法求解途径，是人工智能、数理逻辑、运筹学等领域的交叉学科。

现实世界当中，很多问题都可以用各种形式的约束求解技术来描述和建模。历史上，图灵最早提出图灵机，也是为了解决谓词逻辑约束的可满足性判定问题。人工智能当中的知识推理很多也都最终归结为逻辑约束的可满足性和有效性问题。

人们可以将现实世界中的问题描述、建模为各种形式的数学约束，通过约束求解方法解决这些问题。根据约束表达的方式，常见的约束语言包括SAT（命题逻辑）、MP（数值约束）、SMT（谓词逻辑），CSP（泛化的约束满足问题）等，适用于不同的场景。根据问题的目标，约束求解问题可分为判定问题（判定是否存在解）和优化问题。

SAT 指的是「布尔可满足性问题」，它是世界上第一个被证明的 NP 完全问题。SAT 询问给定布尔公式的变量是否可以一致地用值TRUE或FALSE替换，使得公式计算结果为TRUE。如果是这种情况，公式称为可满足。另一方面，如果不存在这样的赋值，则对于所有可能的变量赋值，公式表示的函数为FALSE，并且公式不可满足。

MP 指的是「数学规划」问题，旨在求得满足约束条件的数值 x* 使 f(x*) 最优，此时 x* 为数学规划问题的最优解，f*=f(x*) 为最优值。数学规划的研究分支包括线性规划、非线性规划、对偶规划、几何规划、整数规划、动态规划及多目标规划等。SAT 可以被看做「0-1」整数规划问题。

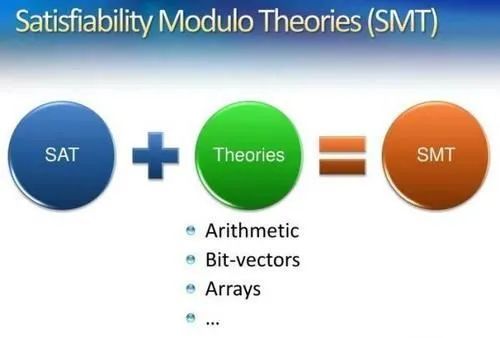
SMT 指的是「可满足性模理论」，用于判定一阶谓词逻辑公式在某些组合背景理论下的可满足性问题。SMT 在命题逻辑的基础上进一步引入了函数和谓词，丰富了其表达能力。我们可以将 SMT 看为SAT 框架与背景理论约束约束（比如线性规划，位向量约束等） 的结合。

CSP 指的是「约束满足问题」，旨在令一组变量都拥有自己的赋值，满足所有关于变量的约束，通过识别违反约束的变量/值的组合迅速缩小大规模的搜索空间。在求解 CSP 问题时，我们需要定义变量集 X、值域集 D、描述变量取值的约束集 C。SAT 是 CSP 问题的简化版。

求解器被称为「工业软件之魂」，约束求解技术被广泛应用于集成电路设计自动化（EDA）、软件分析验证、工业互联网、信息安全、制造与供应链优化等业务场景。求解器对于工业生产、政策制定、资源调度等场景至关重要。然而，从事约束求解研究对于研究者的数理逻辑基础和编程能力都有一定的要求，且学术产出的速度较慢，我国自主可控的求解器研发一度面临着十分艰难的局面，我国的企事业单位严重依赖于使用国外的  Z3和GUROBI等求解器，面临着被「卡脖子」的风险。

进入新世纪，约束求解的相关技术发展十分迅猛，学术界的研究者们开发出了比较成熟的大规模的约束求解器，得到了产业界的高度关注。为了解决「卡脖子技术」的关键环节，以「国产替代」的方式促进先进技术的应用落地正在成为学术界和产业界共同关注和攻关的方向。

在我国约束求解领域研究者的坚守与努力下，自主可控求解器的研发取得了一系列可喜的突破。就在去年，在第十六届国际可满足性模理论比赛(SMT-COMP 2021)上，中国科学院软件研究所研究员、智源学者蔡少伟带领团队研发的求解器荣获整数差分逻辑(QF_IDL)组冠军，这也是中国团队首次在SMT-COMP比赛中获得冠军，该团队也曾多次获得SAT比赛冠军。

杉数科技公司也于 2019 年 5 月推出了中国首个商用线性规划求解器 COPT，华为、阿里巴巴等大厂也纷纷下场布局求解器的研发，国内企业尤其是杉数公司的求解器开始在线性规划榜单的某些benchmark展示出优秀的成绩。这些约束求解器在近年来也在多个重要工业领域得到了应用，包括芯片验证和云计算故障检测（SAT/SMT），各种工业调度场景（数学规划）等。

03

薪火相传，构建生态：约束求解基础与应用训练营

星星之火，可以燎原。就在这一小拨儿人的坚守和努力之下，带动了整个约束求解生态的日渐丰满。

目前，国内各单位的约束求解研究者纷纷行动了起来，这一领域的生态圈日益壮大完善。2022 年 3 月，我国计算机领域的权威期刊《软件学报》设立了题为《约束求解与定理证明》的专刊，截稿时间为 2022 年 9 月 5 日。

为了促进约束求解领域的发展，北京智源人工智能研究院于 2021 年 9 月举办了第一期的约束求解应用封闭研讨「约束求解应用交流会」。这一会议汇聚了包括中国科学院软件研究所研究员、智源学者蔡少伟、阿里达摩院决策智能实验室王孟昌、杉数科技求解器研发总负责人皇甫琦、阿卡思CEO袁军、微软亚洲研究院(MSRA)首席研究员林庆维、华为理论实验室副主任邓益平、华为欧拉实验室形式化验证工程师李屹、京东算法研发部负责人戚永志、北京化工大学经济管理学院马红光在内的国内顶尖的约束求解研究者，参会者分享了各自在该领域的研究进展，商讨了如何构建我国的约束求解生态圈，实现对该领域「卡脖子」技术的突破。

近期，智源研究院与中国计算机学会形式化方法专委会联合举办了36课时的「约束求解基础与应用」训练营，培训时间为 2022 年 4 月 10 日至 2022 年 5 月 29 日，每周末一天。该训练营旨在吸引更多研究者加入到约束求解领域的研究队伍，为我国培养更多的约束求解人才，力求从约束求解的理论基础、核心问题、关键技术及产业应用实践等角度为感兴趣的学生和从业人员提供详细的介绍和指导。该训练营吸引了来自高校和企业的200多人报名，其中报名人数最多的企业和高校分别是华为（26人）和北京大学（23人）。

正如CCF形式化专委会主任王戟在训练营开幕式上所说，「目前我国急需发展工业级别的约束求解技术以及约束求解器，以提升我国在该领域方向上的竞争力。相信此次训练营能够为我国约束求解方向的人才培养、科研和应用发挥重要推动作用，吸引大家进入到这个基础而挑战的方向当中。」

训练营邀请到了中科院软件所蔡少伟研究员、吴志林研究员，中科院计算所李华伟研究员，吉林大学李占山教授，华东师范大学李建文研究员，清华大学贺飞副教授，国防科技大学陈振邦副教授、北京航空航天大学罗川副教授、宁波大学储著飞副教授，杉数科技求解器研发总负责人皇甫琦、华为欧拉实验室形式化验证工程师李屹、阿里达摩院决策智能实验室负责人印卧涛、阿卡斯 CEO 袁军等专家学者。训练营内容包括 SAT、整数规划、CSP、SMT 等基础理论和算法，约束求解在 EDA、软件测试与验证、云计算等领域的应用，以及该领域的前沿进展并展望未来的发展方向。

不积跬步无以至千里。相信未来，求解器这个原本「小众」的领域会焕发生机，吸引更多学术界以及业界的关注，释放出其背后的行业生命力。与此同时随着智能技术的发展和产业数字化转型升级的需求，求解器的应用场景也将不断拓宽，构建出更加完整的产业生态。

报名约束求解基础与应用训练营，请戳「阅读原文」

‍