【管理运筹学】第 6 章 | 运输问题（1，运输问题的数学模型及性质特点）

---

引言

在之前的学习过程中，我们接触的是较为一般性的线性规划问题。但是随着人们对运输——将人或物由一个空间位置移动到另一个空间位置的需求越来越复杂，我们往往在实际生活中会遇到这一类问题，如已知各产地的产量、各销售地的销量以及产地和销地之间的单位运费，如何组织运输方案，使得运量尽可能大而总运费尽可能小。

针对这类线性规划问题，由于其模型结构较为固定，如果利用之前一般性的方法来求解，会比较繁琐和复杂。因此，我们需要另外一种可行而又简便的方法进行求解。

表上作业法便是一种简便而有效的办法，也是我们学习的重点。

---

一、运输问题的数学模型及特点

1.1 运输问题的数学模型

学习如何应用表上作业法前，我们先来了解了解运输问题的数学模型。

举一个典型的例子，设某种物品有 $m$ 个产地（$A_1,A_2,\dots ,A_m$），各产地的产量分别为 $a_1,a_2,\dots ,a_m$ ；有 $n$ 个销地（$B_1,B_2,\dots ,B_n$），各销地的销售能力为 $b_1,b_2,\dots ,b_n$ ；假定从第 $i$ 个产地往第 $j$ 的销地的单位物品的运价为 $c_{ij}$ ，则如何调运这些物品使得总运费最小？

设 $x_{ij}$ 为产地 $A_i$ 运往销地 $B_j$ 的物品数量，若所有产地的总产量和所有销售地的总销量相等，称此问题为产销平衡运输问题，否则，称为产销不平衡运输问题。

对于产销平衡问题，其数学模型可表达为：

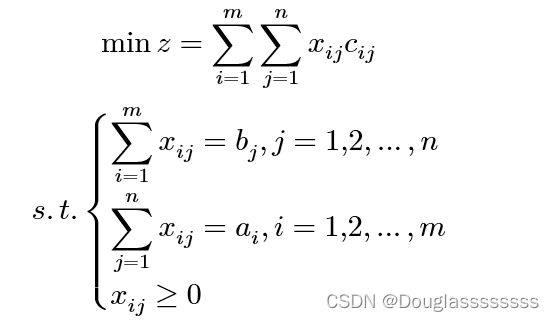
前 $n$ 个约束条件的意义为物品运往某销售地的数量和该销售地的销售数量相同，中间 $m$ 个约束条件的意义为从某产地运往各个销售地的数量和该产地的产量相同，最后 $m\times n$ 个约束条件保证非负条件。

如果用单纯形法进行求解，需要引入很多个人工变量，非常麻烦。

1.2 运输问题的特点

令决策变量 $$x_{ij}^0=\frac{a_i{b}_j}{Q}(i=1,2,\dots ,m;j=1,2,\dots ,n)$$ 其中 $Q={\sum }_{i=1}^m{a}_i={\sum }_{j=1}^n{b}_j$ 。则 $x_{ij}^0$ 为运输问题的一个可行解；同时，模型的目标函数存在下界，因此运输问题必存在有限最优解。

分析 1.1 中的数学模型结构，对约束方程加以整理，可得到运输问题具有如下特点：

• 约束条件系数矩阵等于 0 或 1；
• 约束条件系数矩阵的每一列有两个非零元素，说明每一个变量在前面 $n$ 个约束方程中出现一次，在中间 $m$ 个约束方程中也出现一次。

对于产销平衡运输问题，还具有以下特点：

• 所有约束条件均为等式。
• 各产地产量之和等于各销售地销量之和。

1.3 运输问题的解

运输问题的解代表一个运输方案，其中每一个变量 $x_{ij}$ 的值表示由 $A_i$ 运往 $B_j$ 的物品数量。

可以设想同求一般线性规划问题一样进行求解运输问题，如采用迭代法，即先找出一个基本可行解，再进行解的最优性检验；若它不是最优解，就进行迭代调整，以得到一个更好的解；继续检验和调整改进，直至得到最优解为止。

为了能按照上述思路求解运输问题，要求每一步迭代得到的解 $X$ 必须是可行解，这就意味着：

1. $X$ 必须满足所有约束条件；
2. 基变量对应的约束方程组的系数列向量线性无关；
3. 解中非零变量的个数不能大于 $(m+n-1)$ 个，因为运输问题虽有 $(m+n)$ 个约束方程，但由于总销量等于总产量，故只有 $(m+n-1)$ 个约束方程是线性独立的；
4. 为使得迭代顺利进行，基变量的个数在迭代过程中保持为 $(m+n-1)$ 个。

---

二、表上作业法

表上作业法的求解工作在运输表上进行，运输问题解的每一个分量，都唯一对应其在运输表中的一个格子。它是一种迭代法，迭代步骤为：

先按某种规则找出一个初始解（初始调运方案），得出运输问题的一个基本可行解后，就可将基变量的值 $x_{ij}$ 填入运输表相应的格子内，并将这种格子称为填有数字格（可以含 0 ），非基变量对应格不填，称为空格。

接着对现有的解作最优性判别，若不是最优解，就在运输表上对其进行改进，得出一个新解；再判别，再改进；直至得到运输问题的最优解为止。

---

写在最后

至于具体的方法介绍，我打算放在后面单独说说。